超平面分離定理
超平面分離定理(英語:hyperplane separation theorem)是幾何學中關於n維歐幾里德空間中不相交凸集的定理,有幾個相當相似的版本。在該定理的一種版本中,如果這兩個集合都是閉集並且至少其中一個是緊的,那麼它們之間存在一個超平面,甚至它們之間存在兩個由間隙隔開的平行超平面。 在另一個版本中,如果兩個不相交的凸集都是開集,那麼它們之間有一個超平面,但不一定有任何間隙。 與分離超平面正交的軸是分離軸,因為凸體在該軸上的正交投影是不相交的[1]。
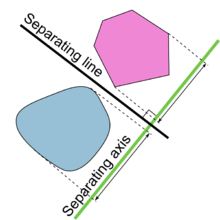 超平面分離定理的圖示 | |
| 類別 | 定理 |
|---|---|
| 領域 | |
| 猜想提出者 | 赫爾曼·閔可夫斯基 |
| 開放問題 | 無 |
| 推廣 | 哈恩-巴拿赫定理 |
超平面分離定理由赫爾曼·閔可夫斯基提出,後哈恩-巴納赫分離定理將結果推廣到拓撲向量空間。在支持向量機的背景下,最佳分離超平面或最大邊緣超平面是分離兩個點凸包並且與兩者等距的超平面[2][3]。
參考資料
編輯- ^ Witten, Ian H.; Frank, Eibe; Hall, Mark A.; Pal, Christopher J. Data Mining: Practical Machine Learning Tools and Techniques Fourth. Morgan Kaufmann. 2016: 253–254. ISBN 9780128043578.
- ^ Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome. The Elements of Statistical Learning : Data Mining, Inference, and Prediction (PDF) Second. New York: Springer. 2008: 129–135 [2023-10-09]. (原始內容存檔 (PDF)於2018-09-28).
- ^ Deisenroth, Marc Peter; Faisal, A. Aldo; Ong, Cheng Soon. Mathematics for Machine Learning. Cambridge University Press. 2020: 337–338. ISBN 978-1-108-45514-5.