维基百科

确定有限状态自动机最小化

將給定的DFA改造為等價且擁有最少狀態的DFA的過程

在自动机理论（计算机科学的一个分支）中，确定有限状态自动机最小化是将给定的确定有限状态自动机（DFA, Deterministic Finite Automaton）改造为等价且拥有最少状态的DFA的过程。这里，两个DFA等价意味着他们识别相同的正则语言。各自动机理论的教材中，已经给出了若干已知的最小化算法。[1]

确定有限状态自动机 (DFA)的一个例子，状态c对任何输入串都和状态d与e有相同的行为。类似地，状态a和b是等价的。这个DFA没有不可达状态。
等价的最小DFA，等价状态都被合并成了一个。

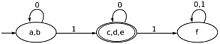
最小DFA

编辑

对于每个正则语言，都存在一个最小自动机接受它，即一个有着最小状态数目的DFA，且这个DFA是唯一的（除去状态命名不同的差别）。[2][3] 最小DFA保证了其在模式匹配等计算应用中开销的最小。

在不影响原始DFA所接受语言的情况下，有两类状态可以被移除或合并，以实现最小化过程。

  • 不可达状态指DFA在任意输入串下都无法达到的状态。
  • 等价状态指在同一输入串下不产生区别的状态。

DFA最小化通常要经历三个步骤，分别对应于相关状态的移除或合并。因为等价状态的消解开销高昂，通常会将其放到最后一步。

不可达状态

编辑

DFA   的状态   是不可达的，若不存在   上的串  ，使得  。可达状态可以用如下算法来找到： 

let reachable_states := {q0};
let new_states := {q0};
do {
    temp := the empty set;
    for each q in new_states do
        for each c in Σ do
            temp := temp ∪ {p such that p = δ(q,c)};
        end;
    end;
    new_states := temp \ reachable_states;
    reachable_states := reachable_states ∪ new_states;
} while (new_states ≠ the empty set);
unreachable_states := Q \ reachable_states;

将不可达状态从DFA中移去并不会影响其接受的语言。

等价状态

编辑

Hopcroft算法

编辑

根据 Hopcroft (1971)，以下算法可用来合并等价状态。该算法基于划分细化，按照状态的行为将DFA各状态分组。这些分组即Myhill-Nerode等价关系下的等价类，满足同一等价类中的两个状态在相同的输入下有相同的行为。即对划分中属于同一等价类的任意两个状态   和  ，对所有输入串  ，  所导致的转移应当始终将   和   带到相同的状态，或都接受，或都拒绝。而不应当出现   将   带到了一个接受状态，而将   带到了一个拒绝状态，反之亦然。

下面以伪代码形式描述了该算法： 

P := {F, Q \ F};
W := {F};
while (W is not empty) do
     choose and remove a set A from W
     for each c in Σ do
          let X be the set of states for which a transition on c leads to a state in A
          for each set Y in P for which X ∩ Y is nonempty and Y \ X is nonempty do
               replace Y in P by the two sets X ∩ Y and Y \ X
               if Y is in W
                    replace Y in W by the same two sets
               else
                    if |X ∩ Y| <= |Y \ X|
                         add X ∩ Y to W
                    else
                         add Y \ X to W
          end;
     end;
end;

算法从一个粗划分开始：在Myhill–Nerode关系下等价的状态对都属于划分中的同一子集，但此时不等价的状态对也可能被划入了同一子集。 上述算法逐渐将划分细化为大量较小的集合，每一步都将各状态集分为不等价的一对子集。起始划分是将那些明显没有相同行为的状态分为接受状态和拒绝状态。随后算法在每一轮都会从当前划分中选中一个集合   和一个输入符  ，再将划分中的每个集合分成两个子集（可能为空）：在输入   下可以被带到   中状态的状态，和在输入   下不会被带到   中状态的状态。由于   已知和划分中其他集合具有不同的行为，  的子集也具有该性质。当找不到细分的时候，算法终止。

最坏情况下，算法的运行时间是  ，其中   为状态数，  为字母表大小。这一时间界的得出是由于，对自动机的每   个转移，每步转移在切分步骤中参与了   的复杂度。划分细分的数据结构可以允许每步切分的操作时间和转移次数成比例。[4] 这一算法仍是解决该问题的已知最有效算法，对某些输入的随机分布，算法平均复杂度的时间界要更好，为  .[5]

当Hopcroft算法已经将DFA中的状态划分为等价类，最小DFA就可以通过为每个等价类生成一个状态来构造了。若   是划分   的一个状态集，  是   中的一个状态，  是一个字符输入；那么最小DFA的状态转移从   起始，在   下转移到原自动机从状态   在输入   下转移到的状态集。最小DFA的起始状态是包含有原DFA起始状态的集合，接受状态是其成员为原DFA中接受状态的集合。

Moore算法

编辑

Moore DFA最小化算法由Edward F. Moore （1956） 给出。与 Hopcroft 算法类似地，它维护一个划分，且这个划分的初值为接受和拒绝状态的划分，并同样反复细化直至无法继续细化。在每一步中，它都会用 s + 1 个划分的最粗公细化 (coarsest common refinement) 来替代当前的划分，这   个划分中的一个是当前划分，其他的   个则是当前划分在转移函数和在所有输入符号下的原象。当这一操作无法改善当前划分时，算法即停止。这个算法在最坏情况下的复杂度是  ：算法的每个步骤都需要  ，这是基数排序一个变种用以重排状态的复杂度，状态重排使得新划分下同一集合中状态的编号顺序是接连的。又，最多会有   轮，因为除最后一轮外，每轮都使得划分中的集合数目增加。在Moore算法下导致最坏情况的DFA最小化问题实例和Hopcroft算法是相同的。算法的轮数会比   小得多，所以平均上（  是常数），其性能可达   甚至  ，结果取决于建模平均情况行为的自动机随机选取分布方式。[6]

Brzozowski算法

编辑

Brzozowski (1963) 注意到，将DFA的边反转将产生一个原语言反序的非确定有限状态自动机 (NFA)。再将这个NFA用标准的幂集构造法（只构造转换后DFA的可达状态）转换为DFA，就会产生原语言反序的最小DFA。重复反转操作，就可以得到原语言的最小DFA。Brzozowski算法在最坏情况下的复杂度是指数的，因为存在这样的正则语言，其反序的最小DFA的规模是原语言DFA规模的指数大。[7] 但通常来说这个算法比最坏情况表现得要好。

NFA最小化

编辑

以上的步骤都对DFA有效，可是划分的方法并不适用于非确定有限状态自动机 (NFA)。[8]虽然穷举搜索可以最小化NFA，但并没有一个多项式时间的算法可以完成该过程，除非 P=PSPACE（计算复杂性理论中的一个未解决问题，一般认为很可能P≠PSPACE）。然而的确存在比暴力搜索可能更加有效的NFA最小化算法。[9]

参见

编辑

注释

编辑
  1. ^ Hopcroft, Motwani & Ullman (2001), Section 4.4.3, "Minimization of DFA's".
  2. ^ Hopcroft & Ullman (1979), Section 3.4, Theorem 3.10, p.67
  3. ^ Hopcroft, Motwani & Ullman (2001), Section 4.4.3, "Minimization of DFA's", p. 159, and p. 164 (remark after Theorem 4.26)
  4. ^ Hopcroft (1971); Aho, Hopcroft & Ullman (1974)
  5. ^ Berstel et al. (2010).
  6. ^ David (2012).
  7. ^ For instance, the language of binary strings whose nth symbol is a one requires only n + 1 states, but its reversal requires 2n states. Leiss (1981) provides a ternary n-state DFA whose reversal requires 2n states, the maximum possible. For additional examples and the observation of the connection between these examples and the worst-case analysis of Brzozowski's algorithm, see Câmpeanu et al. (2001).
  8. ^ Hopcroft, Motwani & Ullman (2001), Section 4.4, Figure labeled "Minimizing the States of an NFA", p. 163.
  9. ^ Kameda & Weiner (1970).

参考文献

编辑

外部链接

编辑
检索自“https://zh.wikipedia.org/w/index.php?title=确定有限状态自动机最小化&oldid=71758407”