完全二分图

完全二分图是一种特殊的二分图，可以把图中的顶点分成两个集合，使得第一个集合中的所有顶点都与第二个集合中的所有顶点相连。

完全二分图
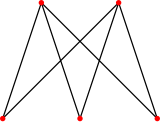一个完全二分图m=3 n =2
顶点	n+m
边	mn
自同构群	2m!n!如果m=n，否则m!n!

定义

完全二分图$G:=(V_{1}+V_{2},E)$是一个二分图，使得对于任何两个顶点$v_{1}\in V_{1}$和$v_{2}\in V_{2}$，$v_{1}v_{2}$都是$G$中的一条边。$\left|V_{1}\right|=m$且$\left|V_{2}\right|=n$的完全二分图记为$K_{m,n}$。

例子

• 
  K_1,3
• 
  K_2,3
• 
  K_3,3

性质

• 平面图不能含有子图$K_{3,3}$；外平面图不能含有子图$K_{3,2}$（这些是必要条件而不是充分条件）。
• 完全二分图$K_{m,n}$的顶点覆盖数为$\min \lbrace m,n\rbrace$，边覆盖数为$\max \lbrace m,n\rbrace$。
• 完全二分图$K_{m,n}$具有大小为$\max \lbrace m,n\rbrace$的最大独立集。
• 完全二分图$K_{m,n}$具有大小为$\min \lbrace m,n\rbrace$的最大匹配。
• 完全二分图$K_{n,n}$具有正则的n-边染色。
• 完全二分图$K_{m,n}$有m^n-1 n^m-1个不同的生成树。

参见

• 圈图
• 道路 (图论)
• 完全图
• 零图
• 二分图
• 三间小屋问题