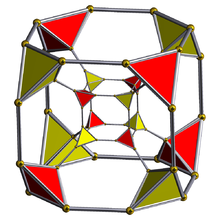
截角超立方体
| 截角超立方体 | |
|---|---|
 | |
| 类型 | 均匀多胞体 |
| 识别 | |
| 名称 | 截角超立方体 |
| 参考索引 | 12 13 14 |
| 数学表示法 | |
| 考克斯特符号 | |
| 施莱夫利符号 | t0,1{4,3,3} |
| 性质 | |
| 胞 | 24 8 3.8.8 16 3.3.3 |
| 面 | 88 64 {3} 24 {8} |
| 边 | 128 |
| 顶点 | 64 |
| 组成与布局 | |
| 顶点图 |  Isosceles triangular pyramid |
| 对称性 | |
| 考克斯特群 | BC4, [4,3,3], order 384 |
| 特性 | |
| convex | |
坐标
编辑截角超立方体可以通过在每条棱距离顶点 处截断超立方体的每一个角来得到。每个截断的角会产生一个正四面体。
一个棱长为2的截角超立方体的每个顶点的笛卡儿坐标系坐标为:
投影
编辑| 考克斯特平面 | B4 | B3 / D4 / A2 | B2 / D3 |
|---|---|---|---|
| Graph | |||
| 二面体群 | [8] | [6] | [4] |
| 考克斯特平面 | F4 | A3 | |
| Graph | |||
| 二面体群 | [12/3] | [4] |
| 展开图 |
三维正交投影 |
参考文献
编辑- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- H.S.M. Coxeter:
- Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] (页面存档备份,存于互联网档案馆)
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- 2. Convex uniform polychora based on the tesseract (8-cell) and hexadecachoron (16-cell) - Models 13, 16, 17, George Olshevsky.
- Klitzing, Richard. 4D uniform polytopes (polychora). bendwavy.org. o3o3o4o - tat, o3x3x4o - tah, x3x3o4o - thex
外部链接
编辑- Paper model of truncated tesseract (页面存档备份,存于互联网档案馆) created using nets generated by Stella4D software