维基百科

拉胀材料

是泊松比为负值的结构或材料

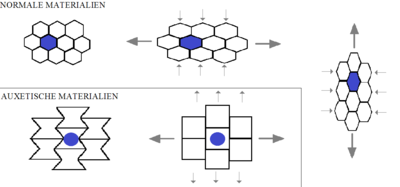
拉胀材料（Auxetics）也称为负泊松比材料，是泊松比为负值的结构或材料[1]。一般材料在拉伸时，垂直于拉伸方向的部分会收缩。但拉胀材料在拉伸时，垂直拉伸方向的部分会膨胀，这是因为其特殊内部构造，以及在单轴施力下的形变方式有关。拉胀材料可能是单分子、晶体，或是特别的巨观结构。

拉胀材料

有拉胀特性的材料及结构多半会有高吸震及高断裂抵抗的能力。拉胀材料可用在像防弹背心[2]、包装材料、护膝及护肘、强健吸震材料及胶棉拖把。

历史

编辑

auxetic一词源自希腊文的αὐξητικός（auxetikos），意思是“倾向于增加”。这个词是由艾希特大学的Ken Evans教授所创[3][4]。

由柏林的研究者K. Pietsch在1978年发明的RFS结构（钻石折叠结构），是首批人工合成的拉胀材料之一[5]，K. Pietsch没有使用auxetic一词，不过他第一个描述其底层的杠杆特性以及其非线性的力学特性，因此视为是拉胀网状材料的发明者。 最早发表的负泊松常数论文是由A. G. Kolpakov在1985年提出《确认弹性网络的平均特性》（Determination of the average characteristics of elastic frameworks）。下一个有关合成拉胀材料的论文是在1987年的《科学》期刊，标题是《负泊松比的泡沬结构》（Foam structures with a Negative Poisson's Ratio）[6]，是威斯康星大学麦迪逊分校的R.S. Lakes所提出。auxetic一词的使用大约是在1991年开始[7]。在1985年开始发表用周期性凹六边形单元（有负泊松比特性）建构复合结构的设计[8][9][10][11]。

特性

编辑
 
有拉胀材料的鞋子，在走路或跑步时其大小会改变

一般而言，拉胀材料是低密度的物质，因此其中允许有类似杠杆，可以变形的拉胀微结构[12]。

巨观下，拉胀特性可以用非弹性的弦绕在弹性的绳子上来说明。当结构的末端受力拉开时，非弹性的弦伸直，弹性绳伸展并绕在其周围，因此增加了结构的有效体积。巨观下的拉胀特性也可以用来开发有强化机能的产品，例如由Grima及Evans开发，以拉胀可旋转三角形结构为基础的鞋子[13][14][15]

常见的拉胀材料

编辑

以下一些拉胀材料的例子：

  • 拉胀聚氨酯泡沫[16][17]。
  • α-方硅石（英语：Cristobalite）[18]。
  • 特定的岩石及矿物[19]。
  • 石墨烯，可以透过引入晶格空位使其有拉胀性[20][21]。
  • 活的动物骨骼组织（这个只是推测）[19]。
  • 在正常运动范围内的肌腱[22]。
  • 特殊的聚四氟乙烯聚合物，例如Gore-Tex[23]。
  • 一些特殊的纸张。若纸张在平行纸面的方向受力拉伸，由于其网状的结构，其厚度也会增加[24][25]
  • 一些折纸形成的结构，例如钻石折叠结构（Diamond-Folding-Structure、也简称为RFS）、人字纹（英语：Herringbone pattern）折叠结构（FFS）或是三浦折叠[26][27]，或是由这些折叠衍生的周期性图案[28][29]。
  • 一些为呈现负泊松比而设计的特制结构[30][31]。
  • 链状有机分子。近期的研究发现像是n-烷烃或是类似结构的有机晶体可能会有拉胀特性[32]。
  • 加工过的针刺不织布。因为其纤维的网状结构，应用热和压力的加工方案可以让不织布具有拉胀特性[33][34]。

木栓不是拉胀材料，但其泊松比几乎为0，因此适合用来作酒瓶的瓶塞[35][36]

相关条目

编辑

参考资料

编辑
  1. ^ Nana Ho. 柚子帽是真的！BMW 參考柚子皮結構做防護配件，保護性能提升 20%. 科技新报. 2017-10-04 [2019-08-08]. （原始内容存档于2019-08-07）. 
  2. ^ Hook's law. The Economist. 2012-12-01 [2013-03-01]. （原始内容存档于2013-02-28）. 
  3. ^ Quinion, Michael, Auxetic, 1996-11-09 [2009-01-02], （原始内容存档于2009-02-17） .
  4. ^ Evans, Ken, Auxetic polymers: a new range of materials., Endeavour, 1991, 15 (4): 170–174, doi:10.1016/0160-9327(91)90123-S .
  5. ^ RFS-Struktur (Rauten-Falt-Struktur) （页面存档备份，存于互联网档案馆）, In: Materialblog.de
  6. ^ Lakes, R.S., Foam structures with a negative Poisson's ratio, Science, 1987-02-27, 235 (4792): 1038–40, Bibcode:1987Sci...235.1038L, PMID 17782252, doi:10.1126/science.235.4792.1038. 
  7. ^ Evans, Ken, Auxetic polymers: a new range of materials, Endeavour, 1991, 15 (4): 170–174, doi:10.1016/0160-9327(91)90123-S .
  8. ^ Kolpakov, A.G. Determination of the average characteristics of elastic frameworks. Journal of Applied Mathematics and Mechanics. 1985, 49 (6): 739–745. Bibcode:1985JApMM..49..739K. doi:10.1016/0021-8928(85)90011-5. 
  9. ^ Almgren, R.F. An isotropic three-dimensional structure with Poisson's ratio=-1. Journal of Elasticity. 1985, 15 (4): 427–430. doi:10.1007/bf00042531. 
  10. ^ Theocaris, P.S.; Stavroulakis, G.E.; Panagiotopoulos, P.D. Negative Poisson's ratio in composites with star-shaped inclusions: a numerical homogenization approach .. Archive of Applied Mechanics. 1997, 67 (4): 274–286. Bibcode:1997AAM....67..274T. doi:10.1007/s004190050117. 
  11. ^ Theocaris, P.S.; Stavroulakis, G.E. The homogenization method for the study of variation of Poisson's ratio in fiber composites. Archive of Applied Mechanics. 1998, 69 (3–4): 281–295. Bibcode:1998AAM....68..281T. doi:10.1007/s004190050165. 
  12. ^ A stretch of the imagination - 7 June 1997 - New Scientist Space. [2019-08-07]. （原始内容存档于2015-05-01）. 
  13. ^ Grima, JN; Evans, KE. Auxetic behavior from rotating squares. Journal of Materials Science Letters. 2000, 19 (17): 1563–1565. doi:10.1023/A:1006781224002. 
  14. ^ Grima, JN; Evans, KE. Auxetic behavior from rotating triangles. Journal of Materials Science. 2006, 41 (10): 3193–3196. Bibcode:2006JMatS..41.3193G. doi:10.1007/s10853-006-6339-8. 
  15. ^ Nike Free 2016 product press release. （原始内容存档于2018-11-05）. 
  16. ^ Li, Yan; Zeng, Changchun. On the successful fabrication of auxetic polyurethane foams: Materials requirement, processing strategy and conversion mechanism. Polymer. 2016, 87: 98–107. doi:10.1016/j.polymer.2016.01.076. 
  17. ^ Li, Yan; Zeng, Changchun. Room‐Temperature, Near‐Instantaneous Fabrication of Auxetic Materials with Constant Poisson's Ratio over Large Deformation. Advanced Materials. 2016, 28 (14): 2822–2826. PMID 26861805. doi:10.1002/adma.201505650. 
  18. ^ Yeganeh-Haeri, Amir; Weidner, Donald J.; Parise, John B. Elasticity of α-Cristobalite: A Silicon Dioxide with a Negative Poisson's Ratio. Science. 1992-07-31, 257 (5070): 650–652. Bibcode:1992Sci...257..650Y. ISSN 0036-8075. PMID 17740733. doi:10.1126/science.257.5070.650 （英语）. 
  19. ^ 19.0 19.1 Burke, Maria, A stretch of the imagination, New Scientist, 1997-06-07, 154 (2085): 36 [2019-08-07], （原始内容存档于2015-05-01） 
  20. ^ Grima, J. N.; Winczewski, S.; Mizzi, L.; Grech, M. C.; Cauchi, R.; Gatt, R.; Attard, D.; Wojciechowski, K.W.; Rybicki, J. Tailoring Graphene to Achieve Negative Poisson's Ratio Properties. Advanced Materials. 2014, 27 (8): 1455–1459. PMID 25504060. doi:10.1002/adma.201404106. 
  21. ^ Grima, Joseph N.; Grech, Michael C.; Grima‐Cornish, James N.; Gatt, Ruben; Attard, Daphne. Giant Auxetic Behaviour in Engineered Graphene. Annalen der Physik. 2018, 530 (6): 1700330. Bibcode:2018AnP...53000330G. ISSN 1521-3889. doi:10.1002/andp.201700330 （英语）. 
  22. ^ Gatt R, Vella Wood M, Gatt A, Zarb F, Formosa C, Azzopardi KM, Casha A, Agius TP, Schembri-Wismayer P, Attard L, Chockalingam N, Grima JN. Negative Poisson's ratios in tendons: An unexpected mechanical response. Acta Biomater. 2015, 24: 201–208. PMID 26102335. doi:10.1016/j.actbio.2015.06.018. 
  23. ^ Auxetic materials, 2001-03-09 [2009-01-02], （原始内容存档于2008-08-11） .
  24. ^ Baum et al. 1984, Tappi journal, Öhrn, O. E. (1965): Thickness variations of paper on stretching, Svensk Papperstidn. 68(5), 141.
  25. ^ Verma, Prateek; Shofner, ML; Griffin, AC. Deconstructing the auxetic behavior of paper. Physica Status Solidi B. 2013, 251 (2): 289–296. Bibcode:2014PSSBR.251..289V. doi:10.1002/pssb.201384243. 
  26. ^ Mark, Schenk. Folded Shell Structures, PhD Thesis (PDF). University of Cambridge, Clare College. 2011 [2019-08-07]. （原始内容存档 (PDF)于2017-03-25）. 
  27. ^ Lv, Cheng; Krishnaraju, Deepakshyam; Konjevod, Goran; Yu, Hongyu; Jiang, Hanqing. Origami based Mechanical Metamaterials. Scientific Reports. 2015, 4: 5979. PMC 4124469  . PMID 25099402. doi:10.1038/srep05979. 
  28. ^ Eidini, Maryam; Paulino, Glaucio H. Unraveling metamaterial properties in zigzag-base folded sheets. Science Advances. 2015, 1 (8): e1500224. Bibcode:2015SciA....1E0224E. ISSN 2375-2548. PMC 4643767  . PMID 26601253. arXiv:1502.05977  . doi:10.1126/sciadv.1500224. 
  29. ^ Eidini, Maryam. Zigzag-base folded sheet cellular mechanical metamaterials. Extreme Mechanics Letters. 2016, 6: 96–102. arXiv:1509.08104  . doi:10.1016/j.eml.2015.12.006. 
  30. ^ Tiemo Bückmann; et al. Tailored 3D Mechanical Metamaterials Made by Dip-in Direct-Laser-Writing Optical Lithography. Advanced Materials. 2012-05, 24 (20): 2710–2714. PMID 22495906. doi:10.1002/adma.201200584. 
  31. ^ Grima‐Cornish, James N.; Grima, Joseph N.; Evans, Kenneth E. On the Structural and Mechanical Properties of Poly(Phenylacetylene) Truss-Like Hexagonal Hierarchical Nanonetworks. Physica Status Solidi B. 2017, 254 (12): 1700190. Bibcode:2017PSSBR.25400190G. ISSN 1521-3951. doi:10.1002/pssb.201700190. hdl:10871/31485 （英语）. 
  32. ^ Stetsenko, M. Determining the elastic constants of hydrocarbons of heavy oil products using molecular dynamics simulation approach. Journal of Petroleum Science and Engineering. 2015, 126: 124–130. doi:10.1016/j.petrol.2014.12.021. 
  33. ^ Verma, Prateek; Lin, A; Wagner, KB; Shofner, ML; Griffin, AC. Inducing out-of-plane auxetic behavior in needle-punched nonwovens. Physica Status Solidi B. 2015, 252 (7): 1455–1464. Bibcode:2015PSSBR.252.1455V. doi:10.1002/pssb.201552036. 
  34. ^ Verma, Prateek; Shofner, Meisha L.; Lin, Angela; Wagner, Karla B.; Griffin, Anselm C. Induction of auxetic response in needle-punched nonwovens: Effects of temperature, pressure, and time. Physica Status Solidi B. 2016, 253 (7): 1270–1278. ISSN 1521-3951. doi:10.1002/pssb.201600072 （英语）. 
  35. ^ Stavroulakis, G.E. Auxetic behaviour: Appearance and engineering applications. Physica Status Solidi B. 2005, 242 (3): 710–720. Bibcode:2005PSSBR.242..710S. doi:10.1002/pssb.200460388. 
  36. ^ Kaminakis, N.T.; Stavroulakis, G.E. Topology optimization for compliant mechanisms, using evolutionary-hybrid algorithms and application to the design of auxetic materials. Composites Part B: Engineering. 2012, 43 (6): 2655–2668. doi:10.1016/j.compositesb.2012.03.018. 

外部链接

编辑
检索自“https://zh.wikipedia.org/w/index.php?title=拉脹材料&oldid=68066487”