安定时间
(重定向自整定時間)
安定时间(Settling time)也称为整定时间,是指放大器或控制系统在步阶输入后,输出到达最终值,且其误差可维持在一定范围(一般是会对称于最终值)内的时间,是暂态响应的特性之一。安定时间包括很短的传播延迟,加上输出依照瞬态率振荡到最终值附近的时间,以及最后安定在允许误差附近的时间。
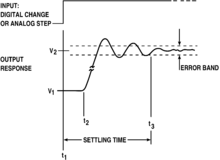
有能量储存的系统无法立即反应,当输入变化或有扰动时会有暂态的现象[1]。
定义
编辑Tay, Mareels and Moore(1997)定义安定时间为“输出到达最终值附近,且和最终值之间的误差维持在一定范围(一般是5%到2%)内所需要的时间。”[2]
数学细节
编辑安定时间和系统响应及时间常数有关。
一阶系统
编辑一阶系统较少定义安定时间,但一阶系统在三倍时间常数后,其输出和稳态的误差降至 ,五倍时间常数后,其输出和稳态的误差降至 [3],一般已可以忽略其误差[4]。
二阶系统
编辑若二阶欠阻尼系统的阻尼比 ,其步阶响应下的安定时间可以用以下式来近似:
因此,误差在2%内的安定时间为:
参考资料
编辑- ^ Modern Control Engineering (5th Edition), Katsuhiko Ogata
- ^ Tay, Teng-Tiow; Iven Mareels; John B. Moore. High performance control. Birkhäuser. 1997: 93. ISBN 0-8176-4004-5.
- ^ 电工技术. 清华大学出版社有限公司. 2001: 98–. ISBN 978-7-302-04927-2.
- ^ 電路學(上). 五南图书出版股份有限公司. : 251–. ISBN 978-957-11-4162-6.
- ^ Richard C. Dorf; Robert H. Bishop. Modern Control Systems. Addison Wesley. 1995: 223. ISBN 0-201-50174-0.
相关条目
编辑外部链接
编辑- Second-Order System Example
- Op Amp Settling Time (页面存档备份,存于互联网档案馆)
- Graphical tutorial of Settling time and Risetime
- MATLAB function (页面存档备份,存于互联网档案馆) for computing settling time, rise time, and other step response characteristics