维基百科

自行

（重定向自自行运动）

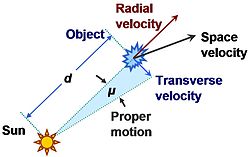
自行是恒星相对于太阳系的质量中心，随着时间变化的推移所显示出在位置在角度上的改变[1]，它的测量是以角秒/年为单位（3600角秒等同于角度的1度）[2]。反之，径向速度是在视线方向上天体接近或远离的速度，随着时间推展的变化率，通常是测量辐射中的多普勒频移。自行不是恒星的本质（即恒星的内禀性质），因为它包含了太阳系本身运动的元素在内[3]。由于光速是有限的，遥远恒星的真实速度很难观测得到，观测自行反映的是恒星当时辐射光的运动。

自行和天体组成速度之间的关系。发射体，该天体与太阳的距离是d，角度的改变率是μ（径/秒），也就是μ = vt / d，而vt = 在太阳视线方向上的横向速度。 (在图说中扫掠过的角度μ和横向速度vt都是单位时间。)

自行的测量需要排除下列会影响观测天体位置座标值的因素，这些因素主要有：

介绍

编辑

在几个世纪的过程中，星星彼此之间似乎都保持着固定的相对位置，因此在有历史的时间里，它们形成的星座也是相同的。例如，大熊座，看起来仍然与数百年前一样。可是，精确的长时间观察显示星座的形状有所改变，每颗恒星都有自己的运动。

这种运动是由恒星相对于太阳的真实运动，和太阳系穿越空间造成的。太阳以大约220公里/秒的速度，在与中心距离大约是8,000±650秒差距的一个近似圆的轨道（称为太阳圈）绕着银河系的中心运动[4][5]，这可以视为银河系本身在此半径上的旋转速度[6][7]。

对自行的测量需要两个量：自行角（位置角）和自行本身。第一个量指示出在天球上运动的方向（以天球北方为0度），90度是朝向东方，余依此类推，第二个量表示运动的程度，单位是毫角秒/年（mas）。

 
自行在天球上的元件：位置角和自行。天球北极点是CNP，春分点是V，恒星在天球上的路径以箭头指示。自行的向量是μ，α = 赤经，δ = 赤纬，θ = 位置角

自行也可以表示为每年在赤经（μα）与赤纬（μδ）上改变的角度。在天球上，位置是以赤经和赤纬设定的。座标的δ对应于纬度，座标的α对应于从春分点V，太阳约在每年3月21日穿越赤道的位置，量度得到的经度[8]。

自行的分量元件如下所显示的，假设某个天体的位置在一年的时间从座标（α, δ）移动到（α1, δ1），并以弧秒为单位测量角度。则每年的角度变化是[9]：

 
 

自行的大小μ是它的元件（分量）向量和[10][11]：

  

此处，δ是赤纬。在算式中的cos δ是因为球体表面至轴的半径事实上是随cos δ而变，例如在极点为0。因此，平行于赤道的速度分量在相当于α的角度，变化是越往北的位置越小。μα 的变化，必须乘上cos δ才能成为自行的分量，他有时称为“赤经自行”，而μδ称为“赤纬自行”[12]。

位置角θ与这些元件相关[13][14]：

   
   

 
从1985年至2005年的巴纳德星，显示每5年的位置变化

巴纳德星是目前所有已知恒星中自行最大的，每年以10.3角秒的速度移动。自行越大，通常暗示一颗星相对离太阳系越近。这的确是巴纳德星的情况，它距离我们只有大约6光年，是除南门二系统（半人马座α三合星）外，距太阳系第二近的恒星。但由于属于红矮星，亮度只有9.54星等的大小，光度微弱，没有大口径望远镜或者高倍双筒望远镜无法观察。

在1992年，天鹰座ρ成为第一颗因为自行而移入另一个星座，导致原有名称无效的恒星，它现在是海豚座的恒星[15]。下一颗这样的恒星将会是雕具座γ，它在2400年将成为天鸽座的恒星[16]。

在1光年的距离上，每年1角秒的自行相当于每秒1.45公里的横向速度。对巴纳德星而言，这相当于每秒90公里；加上每秒111公里的径向速度（垂直于横向速度），可以得到它实际上的运动速度相当于每秒142公里。真实的或绝对的运动速度比自行更难测量，因为真正的横向速度涉及测量自行的时间和距离；也就是说，真正的速度测量取决于距离的测量，而一般很难测量出距离。目前，在邻近的恒星中速度最快的（相对于太阳）是沃夫424，它的速度是每秒555公里（或是光速的1/540）。

在天文学的功用

编辑

有高自行的恒星多半是邻近的恒星，而大多数的恒星都远得足以使他们的自行变得很小，数量级为每年只有数毫角秒。高自行的恒星可以经由相隔数年的巡天摄影获得样品的结构。帕洛玛巡天是这种图像的来源之一。在过去，搜寻高自行的天体都是使用眼睛透过闪烁比对器比对影像，但使用现代化的技术更有成效，像是图像差分，自动搜索数字化的影像资料。由于选择偏误的结果，高自行的样品是易于理解和高质量的，它或许可以用来建立恒星族群的普查 － 例如，在每个真实的光度星等有多少的恒星。这一类的研究可以显示在本地群的恒星族群，主要是本质暗淡、不显眼的恒星，像是红矮星。

在遥远的恒星系统中，像是球状星团，量测大量恒星自行的样本，经由莱昂纳德·梅里特质量估计可以用来计算集团的总质量。与恒星的径向速度结合在一起，自行可以用来计算集团的距离。

利用恒星自行已经推算出银河中心存在着超大质量黑洞[17]。这个黑洞被怀疑就是人马座A*，质量为2.6×106 M☉，此处的M☉是太阳质量。

Röser曾仔细的研究本星系群星系的自行[18]。在2005年，第一次测量出三角座星系M33的自行。M33是本星系群第三大的星系，也是唯一的普通螺旋星系，与银河系的距离约为860± 28千秒差距[19]。虽然知道距离大约786千秒差距的仙女座大星系也在运动，并且预测在50至100亿间会发生仙女-银河碰撞，但是它的自行仍然不清楚，而估计横向速度的上限大约是100公里/秒[7][20][21]。在1999年，猎犬II星系群中的星系NGC 4258（M106）的自行被用来测量这个星系群的精确距离[22]。测量星系的径向运动，直接可以知道该星系是向我们接近还是远离，并且假设集团中只有自行的物体也适用同样的运动，由观测到的自行测量到这个星系群的距离为7.2±0.5 Mpc[23]。

历史

编辑

早期的天文学家（公元400年的马克罗比乌斯（ Macrobius））曾经怀疑恒星有自行。但是直到1718年爱德蒙·哈雷注意到天狼星、大角星和毕宿五的位置与约1850年前的古希腊天文学家伊巴谷所描述的位置有半度以上的偏差，才得到证实[24]。

“自行”这个名词源自法文的propre，意思是“归属于”，所以在天文学中没有“不当运动”这样的名词[1]。

在2005年发表的研究报告，现代天文学家已测出第一个外星系（三角座星系）的自行运动数据。

已知自行最大的恒星

编辑

下表是在《依巴谷星表》内已知自行最大的一些恒星，[25]但不包含像蒂加登星那些虽在星表中，但光度太暗淡的恒星。

高自行的恒星[26]
# 恒星 自行 径向
速度
(公里/秒) 		视差
(mas)
μα·cos δ
(mas/yr) 		μδ
(mas/yr)
1 巴纳德星 -798.71 10337.77 -106.8 549.30
2 卡普坦星 6500.34 -5723.17 +245.5 255.12
3 葛鲁姆布里吉1830 4003.69 -5814.64 -98.0 109.22
4 拉卡伊9352 6766.63 1327.99 +9.7 303.89
5 格利泽1（CD -37 15492） 5633.95 -2336.69 +23.6 229.32
6 HIP 67593 2282.15 5369.33 — 76.20
7 天鹅座61 A & B 4133.05 3201.78 -64.3 287.18
8 拉兰德21185 -580.46 -4769.95 -85.0 392.52
9 印第安座ε 3961.41 -2538.33 -40.4 275.79

软件

编辑

有许多的软件产品，它们可以让人们查看不同时间尺度下的恒星自行。下面是两个免费的：

  • Moovastar –自由软件，视窗板，非常基础的。你可以选择天空中的一个区域，设定极限星等和时间的序列（时间间隔、时间步数、数量步数）。这个程式将模拟恒星的运动，并有清楚的功能说明。
  • HippLiner （页面存档备份，存于互联网档案馆） -自由软件，视窗板，有些复杂，有一些漂亮的显示。仍在发展，须要有更多的导航和功能配置。

相关条目

编辑

参考文献

编辑
  1. ^ 1.0 1.1 Theo Koupelis, Karl F. Kuhn. In Quest of the Universe. Jones & Bartlett Publishers. 2007: 369. ISBN 0763743879. 
  2. ^ Simon F. Green, Mark H. Jones. An Introduction to the Sun and Stars. Cambridge University Press. 2004: 87. ISBN 0521546222. 
  3. ^ D. Scott Birney, Guillermo Gonzalez, David Oesper. Observational astronomy. Cambridge University Press. 2007: 73. ISBN 0521853702. 
  4. ^ Horace A. Smith. RR Lyrae Stars. Cambridge University Press. 2004: 79. ISBN 0521548179. 
  5. ^ M Reid, A Brunthaler, Xu Ye; et al. Mapping the Milky Way and the Local Group. F. Combes, Keiichi Wada (编). Mapping the Galaxy and Nearby Galaxies. Springer. 2008. ISBN 0387727671. 
  6. ^ Y Sofu & V Rubin. Rotation Curves of Spiral Galaxies. Ann. Rev. Astron. Astrophys. 2001, 39: 137–174. Bibcode:2001ARA&A..39..137S. arXiv:astro-ph/0010594  . doi:10.1146/annurev.astro.39.1.137. 
  7. ^ 7.0 7.1 Abraham Loeb, Mark J. Reid, Andreas Brunthaler, Heino Falcke. Constraints on the proper motion of the Andromeda galaxy based on the survival of its satellite M33 (PDF). The Astrophysical Journal. 2005, 633: 894–898 [2011-07-26]. Bibcode:2005ApJ...633..894L. arXiv:astro-ph/0506609  . doi:10.1086/491644. （原始内容存档 (PDF)于2017-08-11）. 
  8. ^ D. Scott Birney, Guillermo Gonzalez, David Oesper. Observational Astronomy. Cambridge University Press. 2006: 8. ISBN 0521853702. 
  9. ^ William Marshall Smart, Robin Michael Green. Textbook on Spherical Astronomy. Cambridge University Press. 1977: 252. ISBN 0521291801. 
  10. ^ Charles Leander Doolittle. A Treatise on Practical Astronomy, as Applied to Geodesy and Navigation. Wiley. 1890: 583. 
  11. ^ Majewski, Steven R. Stellar Motions. University of Virginia. 2006 [2007-05-14]. （原始内容存档于2012-01-25）. 
  12. ^ Simon Newcomb. The Stars: A study of the Universe. Putnam. 1904: 287–288. 
  13. ^ D. Scott Birney, Guillermo Gonzalez, David Oesper. op. cit.. 2007: 75. ISBN 9780521853705. 
  14. ^ See Majewski, Steven R. Stellar motions: parallax, proper motion, radial velocity and space velocity. University of Virginia. 2006 [2008-12-31]. （原始内容存档于2012-01-25）. 
  15. ^ Book-Review - Sky Catalogue 2000.0 - V.1 - Stars to Magnitude 8.0 ED.2. 1992 [2008-05-16]. （原始内容存档于2012-12-14）. 
  16. ^ Hamilton Amateur Astronomers. 1996 [2008-05-16]. （原始内容存档于2009-06-08）. 
  17. ^ AM Ghez; et al. The First Measurement of Spectral Lines in a Short-Period Star Bound to the Galaxy's Central Black Hole: A Paradox of Youth. Astrophysical Journal. 2003, 586: L127–L131. Bibcode:2003ApJ...586L.127G. arXiv:astro-ph/0302299  . doi:10.1086/374804. 
  18. ^ Andreas Brunthaler. M33 – Distance and Motion. Siegfried Röser (编). Reviews in Modern Astronomy: From Cosmological Structures to the Milky Way. Wiley. 2005: 179–194. ISBN 3527406085. 
  19. ^ A. Brunthaler, M.J. Reid, H. Falcke, L.J. Greenhill, C. Henkel. The Geometric Distance and Proper Motion of the Triangulum Galaxy (M33). Science. 2005, 307 (5714): 1440–1443. Bibcode:2005Sci...307.1440B. PMID 15746420. arXiv:astro-ph/0503058  . doi:10.1126/science.1108342. 
  20. ^ Roeland P. van der Marel. M31 Transverse Velocity and Local Group Mass from Satellite Kinematics. The Astrophysical Journal. 2008, 678: 187–199. Bibcode:2008ApJ...678..187V. doi:10.1086/533430. [失效链接]
  21. ^ Manuel Metz, Pavel Kroupa, Helmut Jerjen. The spatial distribution of the Milky Way and Andromeda satellite galaxies. Mon. Not. Roy. Astron. Soc. 2007, 374: 1125–1145. Bibcode:2007MNRAS.374.1125M. arXiv:astro-ph/0610933  . doi:10.1111/j.1365-2966.2006.11228.x. 
  22. ^ Steven Weinberg. Cosmology. Oxford University Press. 2008: 17 [2020-10-10]. ISBN 978-0-19-852682-7. （原始内容存档于2021-05-01）. 
  23. ^ J. R. Herrnstein; et al. A geometric distance to the galaxy NGC4258 from orbital motions in a nuclear gas disk. Nature. 1999, 400 (6744): 539–541. Bibcode:1999Natur.400..539H. arXiv:astro-ph/9907013  . doi:10.1038/22972. 
  24. ^ Otto Neugebauer. A History of Ancient Mathematical Astronomy. Birkhäuser. 1975: 1084. ISBN 354006995X. 
  25. ^ Staff. The 150 Stars in the Hipparcos Catalogue with Largest Proper Motion. ESA. September 15, 2003 [2007-07-21]. （原始内容存档于2013-07-07）. 
  26. ^ SIMBAD. Centre de Données astronomiques de Strasbourg. [2007-07-21]. （原始内容存档于2019-05-30）. 

外部链接

编辑
检索自“https://zh.wikipedia.org/w/index.php?title=自行&oldid=84556660”