视差
视差(英语:parallax,来自古希腊语 παράλλαξις(parallaxis),意即:“差异”)是指从两个不同位置观察同一个物体时,此物体在视野中的位置变化与差异[1][2]。从两个观察点看目标,两条视线之间的夹角叫做这两个点的视差角,两点之间的距离称作视差基线。
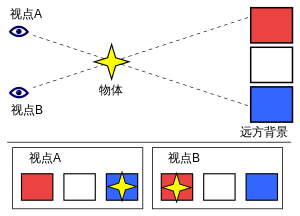

从同样的两个观察点看,目标物体距离越近就有越大的视差,因此视差可以被用来反向估算物体的距离。比如天文学家使用视差的原理测量天体距离地球的距离,包括月球、太阳和在太阳系之外的恒星。例如,依巴谷卫星测量了超过100,000颗邻近恒星的距离。这为天文学提供了测量宇宙距离尺度的阶梯,是其它测距方法的基础。在此处,"视差"这个名词是两条到恒星的视线交角的角度或半角度。
一些光学仪器,像是双筒望远镜、显微镜、和双反相机,会以略为不同的角度观看物体,都会受到视差的影响。许多动物的两只眼睛有着重叠的视野,可以利用视差获得深度知觉;此一过程称为立体视觉。这种效果在电脑视觉用于电脑立体视觉,并有一种装置称为视差测距仪,利用它来测量发现目标的距离,也可以改变为测量目标的高度。
一个简单的,日常都能见到的视差例子是,汽车仪表板上"指针"显示的速度计。当从正前方观看时,显示的正确数值可能是60;但从乘客的位置观看,由于视角的不同,指针显示的速度可能会略有不同。
视知觉
编辑如同人类和其他动物的双眼都在头上不同的位置,它们提供了不同的观点。这是立体视觉的基础,在这个过程中,大脑接收了不同的讯息,从而获得深度知觉,并从两眼的视差估计到物体的距离[3]。有些动物会利用运动视差,这些动物依靠移动(也许只是头部)来获得不同的观点。例如,鸽子(它们两眼的视场没有重叠,因此没有立体视觉)上下摆动头部以获得深度[4]。
视差的应用
编辑视差在应用上根据不同需要派生出各个稍有不同的概念:
- 物理学中,指在不同位置观察远近两物体时,它们间发生相对位置变化的现象。
- 天文学中,指因为观测者位置的移动或由不同地点观测同一天体而引起的方向变化;测量天体视差是确定天体之间距离最基本的方法。天文学家在早期使用此方法测量了月球(从纽约和华盛顿拍摄的照片分析)离地球的距离与天鹅座61的距离。
- 摄影测量中,指立体像对上同名像点的坐标差,其横坐标差称为“左右视差”,纵坐标差称为“上下视差”;在航空摄影测量中,左右视差可以推算地面点之间的高差,上下视差可用以确定像片之间在摄影时的相对关系。
- 摄影术中,指从相机取景器中看到的物体位置和镜头摄入的物体位置不相一致的现象;相机距物体越远,视差越小;高级取景器有校正视差的机能,使物体在感光成像上的位置和从取景器中所看到的位置无论远近都相合;单反相机由于取景器和摄影通过同一物镜,所以基本没有视差。
天文学的距离测量
编辑恒星视差
编辑在星际的尺度,视差的创建来自地球在轨道上不同的位置导致邻近的恒星相对于遥远天体的移动。通过观测视差,测量角度和使用几何学,可以确定到不同天体的距离。当被讨论的天体是恒星时,这种效应称为恒星视差。
恒星视差最常被使用的是周年视差,定义是从地球和太阳观察恒星的视角差,也就是以地球绕太阳的平均轨道半径看一颗恒星在对角的角度。1秒差距(3.26光年)被定义为周年视差为1角秒的距离。周年视差一般是通过观察恒星在年的不同时间,随着地球在它的轨道上移动测量的。周年视差是第一个最可靠的测量最接近恒星的方法。第一个成功测量到的恒星视差是白塞耳在1833年使用量日仪测量的天鹅座61[5]。恒星视差依然是校准其他测量方法的标准。精确测量距离的基础是恒星视差,它需要测量地球到太阳的距离,而现在是以雷达在行星表面的反射来测量[6]。
在这些计算中所涉及的角度都很小,因此很难测量。距离太阳最近的恒星(因此这颗恒星有最大的视差),比邻星,周年视差是0.7687±0.0003角秒[7]。这相当于从5.3公里之外观察直径2公分大小物体的弦所形成的角。
恒星视差是如此的小,因此在无法观测到恒星视差的年代,“恒星视差不存在”被作为反对日心说的主要科学论证。很明显的,如果星星的距离够远,从欧几里得的几何学是无法察觉的,但由于种种的原因,使这种巨大的距离难以置信:其中之一是为了使缺乏视差的恒星能够相容,土星轨道和第八领域(恒星)之间必须有巨大而不太可能存在的空隙,使得第谷成为哥白尼日心说的主要反对者[8]。
在1989年,依巴谷卫星发射的主要目的就是观察近距离恒星的视差和自行,这种方法使数量增加了10倍。即便如此,依巴谷卫星能测量出视差角的恒星距离也只能达到1,600光年,相较于银河系的直径只比1%多了一点。欧洲空间局的盖亚任务,预计在2012年升空,在2013年上线,能够让视差角的测量精确度达到10微秒,将能够绘制出邻近地球数万光年内恒星(与潜在行星)的位置图[9]。
算法
编辑以视差来测量距离在三角学的原则上是一种特殊状况,如果要解出在网络中三角形所有的边和角,除了网络中所有的角,至少有一边的长度必须被测量。因此,仔细测量过长度的一条基线可以解决整个三角网的规模。对视差而言,这个三角形是极其细长和狭窄的,测量的是最短的边(观测者的移动)和非常小的角(永远都小于1角秒[5],其余的两个角都接近90度),要测量的是长边(实际上这两边的长是相同)。
假设这个角度很小(见下文的#推导),一个天体的距离(以秒差距量度)是视差(以角秒量度)的倒数: 。例如,比邻星的距离是1/0.7687=1.3009秒差距(4.243光年)[7]。
周日视差
编辑周日视差是由地球自转或在地球上不同地点观察产生的视差。从地球上不同的地点观测(在给定的同一时刻),月球和较小的类地行星或小行星会出现在背景天恒星上的位置会有所不同[10][11]。
月球视差
编辑月球视差(通常是月球地平视差或月球赤道地平视差的缩写),是(周日)视差的一个特殊例子:月球,是最靠近地球的天体,拥有迄今所有天体中最大的视差,可以超过1度[12]。
只要将恒星视差图(上图)的右下略加修改,就可以很好的说明月球视差。将假想的近端星改成月球,底部代表地球绕太阳的圆轨道改成地球的球体,圆圈是地球表面的一圈。然后,相对于背景恒星在位置角上的差异,就是从两个不同位置看见的月球(地平)视差:在给定的时刻,从其中一个位置(就是图中的垂直线),观察到的月球正好在头顶正上方,而另一个位置(从图中的地球表面,大约就是修改前蓝点的位置)观测到的月球正好在地平线上。
月球(地平)视差可以定义为,以地球半径为基线的月球对角[13], 或者是如上被修改的缩小关系图中的角度p。
任何时刻的月球地平视差取决于当时地球到月球的直线距离。由于月球绕地球的轨道如下所示大约是椭圆的轨道和摄动的影响,地月距离会不断的改变。改变的范围在线距离上是56至63.7地球半径,相当于地平视差1度的大小,对应的弧度角是从约61.4’到约至54’[12]。在天文年历和类似的出版品会以表格制作出每天固定时间的月球水平视差和/或线距离,方便天文学家(以前还有领航员),和以这种方法研究月球运动说(Lunar theory)伴随着时间的座标变化。
视差也可以用来确定到月球的距离。
从一个地点测量月球视差的方法是利用月食。完整的地球影子在月球上的视曲率半径等于从月球到地球和太阳距离之间的差别。这个可以看见的半径等于0.75度,从这儿(太阳的视半径是0.25度)可以获得地球的视半径是1度。这将导出地月距离是60个地球半径,或是384,000公里。阿里斯塔克斯是第一个使用这种方法的人[14],之后的依巴谷和托勒密也发现这种方法并用于他们的工作中[15]。右图显示出在以地球为中心且没有自转的行星模型中,地心和静地压的行星系统周日月球视差。它还演示了很重要的一点,观测者不需要运动也可以形成视差,反过来,一些所谓的视差定义,很可能纯粹是由观测者的运动造成的。
另一种方法是在地球上两个不同的地点,在完全相同的时间很精确的撷取两张月球位置的影像,比较相对于背景恒星的位置。使用地球的方位,测量这两个点的方位,和这两个点在地球上的距离,可以用三角学测量月球的距离:
直到此刻,许多人仍然不知道如何计算地球与月球相隔的距离。他们的环境教导他们这个距离是通过视差的观察和测量得到的。如果视差这个字令他们感到迷惑,他们被告知这是从地球半径的两端连接到月球的两条直线的对角。如果他们怀疑这种方法的完备性,他们立刻可以看到的不只是地球到月球平均距离的数值,234,347英里(94,330leagues),并且误差小于70英里(大约30leagues)。
太阳视差
编辑在哥白尼提出日心系统之后,地球绕着太阳公转,它可以建立起一个没有正确尺寸的太阳系模型。若要确定尺寸,它只需要测量在太阳系内一个天体的距离,也就是说,地球到太阳的平均距离(现在称为天文单位,或以AU表示)。当以三角测量发现,从地球中心和表面观测太阳的位置差异,即以地球半径为基线测量太阳的对顶角,这被称为太阳视差。知道太阳视差和地球的平均半径,就能够测量天文单位。首先,这是在估计膨胀宇宙和可见宇宙大小的漫漫长路上的一小步[16]。
测量地球到月球距离最原始的方法是在阿里斯塔克斯的《太阳和月球的距离与大小》一书中提出。他注意到太阳、月球和地球在上弦和下弦会形成直角三角形(月球位于直角上)。然后,他估计出月球、地球和太阳的夹角是87°。使用正确的几何学,但不正确的观测资料,阿里斯塔克斯推论太阳的距离略低于月球距离的20倍。但是,这个角度的正确数值接近89° 50',而太阳的实际距离比月球远了约390倍[14]。他指出月球和太阳有着几乎一样的视角大小,因此它们的直径和与地球的距离有着相同的比值。因此,他也估计太阳比月球大20倍左右;这一结论,尽管源于不正确的资料,但他的逻辑是正确的。他也明确的表示太阳大于地球,这可以支持日心说的模型。
尽管阿里斯塔克斯以正确的几何原理观测视差,但因为观测的不正确导致结果不正确,却也成为估计太阳系大小的基准长达2,000年之久,直到1761年和1769年观测金星凌日后才被改正[14]。这个方法是爱德蒙·哈雷在1716年提出来的,可惜他未能活着看见结果。使用金星凌日的方法由于黑滴现象的影响而不太成功,但由此得到的结果是15,300万公里,与目前接受的14,960万公里,只有2%的差异。
相关条目
编辑参考资料
编辑- ^ Shorter Oxford English Dictionary. 1968.
Mutual inclination of two lines meeting in an angle
- ^ Parallax. Oxford English Dictionary Second Edition. 1989.
Astron. Apparent displacement, or difference in the apparent position, of an object, caused by actual change (or difference) of position of the point of observation; spec. the angular amount of such displacement or difference of position, being the angle contained between the two straight lines drawn to the object from the two different points of view, and constituting a measure of the distance of the object.
- ^ Steinman, Scott B.; Garzia, Ralph Philip. Foundations of Binocular Vision: A Clinical perspective. McGraw-Hill Professional. 2000: 2–5. ISBN 0-8385-2670-5.
- ^ Steinman & Garzia 2000,p. 180.
- ^ 5.0 5.1 Zeilik & Gregory 1998,p. 44.
- ^ Zeilik & Gregory 1998,§ 22-3.
- ^ 7.0 7.1 Benedict, G. Fritz; McArthur, Barbara; Chappell, D. W.; Nelan, E.; Jefferys, W. H.; van Altena, W.; Lee, J.; Cornell, D.; Shelus, P. J.; Hemenway, P. D.; Franz, Otto G. Interferometric Astrometry of Proxima Centauri and Barnard's Star Using [ITAL]HUBBLE SPACE TELESCOPE[/ITAL] Fine Guidance Sensor 3: Detection Limits for Substellar Companions. The Astronomical Journal. 1999-08, 118 (2) [2022-10-13]. Bibcode:1999astro.ph..5318B. ISSN 1538-3881. arXiv:astro-ph/9905318 . doi:10.1086/300975. (原始内容存档于2021-02-27).
- ^ See p.51 in The reception of Copernicus' heliocentric theory: proceedings of a symposium organized by the Nicolas Copernicus Committee of the International Union of the History and Philosophy of Science, Torun, Poland, 1973, ed. Jerzy Dobrzycki, International Union of the History and Philosophy of Science. Nicolas Copernicus Committee; ISBN 978-90-277-0311-8, ISBN 978-90-277-0311-8
- ^ Henney, Paul J. ESA's Gaia Mission to study stars. Astronomy Today. [2008-03-08]. (原始内容存档于2008-03-17).
- ^ Seidelmann, P. Kenneth. Explanatory Supplement to the Astronomical Almanac. University Science Books. 2005: 123–125. ISBN 1891389459.
- ^ Barbieri, Cesare. Fundamentals of astronomy. CRC Press. 2007: 132–135. ISBN 0750308869.
- ^ 12.0 12.1 Astronomical Almanac e.g. for 1981, section D
- ^ Astronomical Almanac, e.g. for 1981: see Glossary; for formulae see Explanatory Supplement to the Astronomical Almanac, 1992, p.400
- ^ 14.0 14.1 14.2 Gutzwiller, Martin C. Moon-Earth-Sun: The oldest three-body problem. Reviews of Modern Physics. 1998-04-01, 70 (2). Bibcode:1998RvMP...70..589G. ISSN 0034-6861. doi:10.1103/RevModPhys.70.589 (英语).
- ^ Webb, Stephen, 3.2 Aristarchus, Hipparchus, and Ptolemy, Measuring the Universe: The Cosmological Distance Ladder, Springer: 27–35, 1999, ISBN 9781852331061. See in particular p. 33: "Almost everything we know about Hipparchus comes down to us by way of Ptolemy."
- ^ Freedman, Wendy L. The Hubble constant and the expansion age of the Universe. Physics Reports. 2000-08,. 333-334 [2022-10-13]. Bibcode:2000PhR...333...13F. ISSN 0370-1573. arXiv:astro-ph/9909076 . doi:10.1016/S0370-1573(00)00013-2. (原始内容存档于2022-10-24) (英语).
- Hirshfeld, Alan w. Parallax: The Race to Measure the Cosmos. New York: W. H. Freeman. 2001. ISBN 0716737116.
- Whipple, Fred L. Earth Moon and Planets. Read Books. 2007. ISBN 1406764132.
- Zeilik, Michael A.; Gregory, Stephan A. Introductory Astronomy & Astrophysics 4th. Saunders College Publishing. 1998. ISBN 0030062284.
外部链接
编辑- Instructions for having background images on a web page use parallax effects (页面存档备份,存于互联网档案馆)
- Actual parallax project measuring the distance to the moon within 2.3% (页面存档备份,存于互联网档案馆)
- BBC's Sky at Night programme: Patrick Moore demonstrates Parallax using Cricket.(Requires RealPlayer)
- Berkely Center for Cosmological Physics Parallax
- Parallax (页面存档备份,存于互联网档案馆) on an educational website, including a quick estimate of distance based on parallax using eyes and a thumb only