费希尔法 (统计学)

费希尔法（英语：Fisher's method），或称费希尔合并概率检验（英语：Fisher's combined probability test）是统计学中用于合并多个p值的方法，由罗纳德·爱尔默·费希尔所创，常应用于元分析。其基本形式是结合源于同一个零假设（H₀）之下多个独立性检验的结果。

以费希尔法合并两个p值（P₁与P₂）。例如，当P₁与P₂皆为0.1时，合并之p值约为0.05。颜色最深的区域表示整体p值小于0.05。

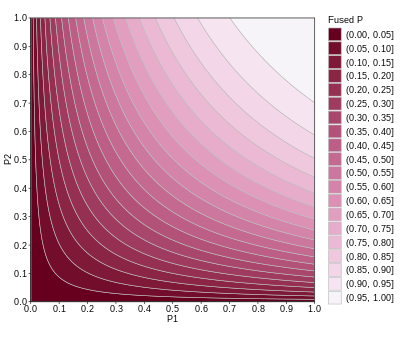
应用

费希尔法用于结合各个检验的极端值概率（即p值）成一个卡方统计量：

$X_{2k}^{2}\sim -2\sum _{i=1}^{k}\ln(p_{i})$，

其中p_i为第i个检验之p值。当p_i较小则卡方统计量X²较大而拒绝整体零假设。

若所有的零假设皆为真，且p_i（或各统计检验量）皆相互独立，则X²服从自由度为2k的卡方分布，其中k表示所有参与的假设检验个数。按此可以取得联合检验之p值，即对多个p值进行合并。

此卡方统计量的分布服从卡方分布的原因是：对于每一个统计检验i，其p值（p_i）服从界于0至1的均匀分布。均匀分布取自然对数的相反数又服从指数分布。指数分布乘2又服从自由度为2的卡方分布。最终，k项独立的卡方统计量（每项自由度为2）之总和服从自由度为2k的卡方分布。

独立性前提的限制

当各检验不独立时，X²偏大、整体p值偏小使推论过分偏好备择假设。因此，在不独立的统计检验量间使用费希尔法时，若整体p值较大较无所谓；但若整体p值很小则可能发生第一类错误。

独立性前提的扩展

主条目：费希尔法的扩展

在统计检验不相互独立时，X²的虚无分布并不单纯。常见的策略是采用缩放过的卡方随机变量近似虚无分布。若已知p值间的协方差，亦存在其它近似方法。

以布朗法为例，该方法可用于结合二个相依p值，当其统计检验量为协方差矩阵已知的多元正态分布。此外，科斯特法扩大了布朗法的条件：协方差矩阵由已知扩展至未知但具标量乘法常数即可。

在相依结构未知时，调和平均p值可以代替费希尔法，但仍不可假设检验相互独立。

结果解读

费希尔法通常用于一系列相互独立的统计检验，例如是具有相同零假设的各别研究。这与元分析的零假设经常是各别的零假设皆为真的情况相符。因此，费希尔法结果若支持备择假设，则可解读为至少存在一个备择假设为真。

在某些情况下，考虑各研究的“异素性”是有意义的，特别是某些研究支持零假设但某些支持备择假设，或是不同研究具有不同的备择假设。不同的备择假设形成的异素性可能是源于效果量在不同研究间不均。例如，考虑一系列针对葡萄糖摄取量对罹患第2型糖尿病的风险之研究，由于各研究间的对象存在遗传或环境上的差异，特定葡萄糖摄取量所对应的罹患风险在各研究间亦可能不同。

在各别备择假设是全真或全伪的情况下，例如检验某种物理定律，单独研究或实验的结果若不一致则是偶然造成的，例如存在统计功效差异。

在元分析中若采用双尾检验，即使部分各别研究指出存在强烈但方向不等的效果，仍可能拒绝整体零假设。在这种情况下，虽然可以解读为至少存在一个研究中的零假设为伪，但这并不意味着应支持所有研究的备择假设。因此，双尾元分析对备择假设中的异素性特别敏感。采用单尾检验的元分析可以检测效果量的异素性，但侧重于单一且预先指定的影响方向。

与斯托夫Z值法的关系

斯托夫Z值法与费希尔法的关系以z与−log(p)的关系表示。

斯托夫Z值法（由社会学家塞缪尔·安德鲁·斯托福所创）与费希尔法的作用相似，但前者可纳入不同研究间具有不同的权重。

令Z_i  =  Φ ^− 1(1−p_i)，其中Φ为标准正态分布的累积分布函数，则

$Z\sim {\frac {\sum _{i=1}^{k}w_{i}Z_{i}}{\sqrt {\sum _{i=1}^{k}w_{i}^{2}}}}$

称为元分析的整体Z值，其中w为各研究的权重。

由于费希尔法基于“平均p值”而斯托夫Z值法基于“平均z值”，二者的关系遵循z与−log(p) = −log(1−Φ(z))的关系。在正态分布之下，二者并非线性关系，但z值经常存在的范围（1至5）之内的关系较线性。因此，二种方法的统计功效通常很接近。

相关条目

• 费希尔法的扩展

外部链接

• metap （页面存档备份，存于互联网档案馆） R套件.