维基百科:台湾教育专案/台大物理系服务学习/112-1/斯托克斯问题
|-
| 斯托克斯问题 || en:Stokes problem || Wu931129(讨论 | 贡献) || 中文条目尚未建立 || ![]() 撰写中⋯⋯ ||
撰写中⋯⋯ ||
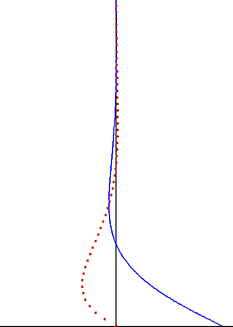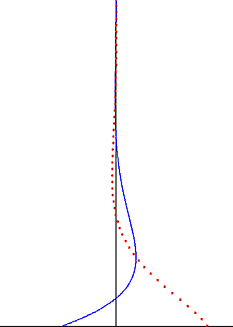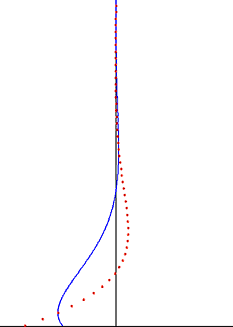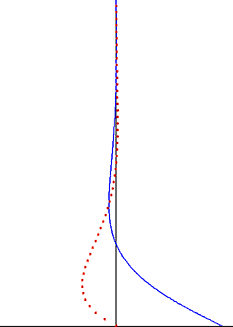
在流体动力学中,斯托克斯问题(斯托克斯第二问题),或常称为斯托克斯边界层和振荡边界层,是个描述受固体平面振荡所影响的流体行为,以乔治·斯托克斯爵士来命名。这是其中一个有精确纳维-斯托克斯方程式解的简单非稳定问题。[1][2] 在湍流中,这问题同样被称为斯托克斯边界层, 但须仰赖实验、数值解与近似法才能得到有用的流体资讯。
考虑一个无限大平面,在 方向以速度 作周期振荡,平面位置为 ,上方充满流体, 是周期振荡的角频率。非压缩性的纳维-斯托克斯方程式可被简化为
其中 为流体的运动黏度。压力梯度未被考虑进此问题中。初始壁上的不滑移条件为
第二个边界条件是因为 的振荡不会影响到无限远处。流体只受平面振荡影响,不考虑压力梯度。
因为周期性,不须考虑初始条件。因为方程式与边界条件皆是线性的,速度函数可以写成某个虚数函数的实数部分
因为
将上式带入偏微分方程式中,可简化为
将边界条件带入
即可得到上式方程式的解为
受振荡平面所影响的扰动以波的形式传播流体,但会受指数项衰减。波的渗透深度 随振荡频率下降而上升,随着运动黏度下降而下降。
单位面积因流体而施加在平面上的力为
在力与平面的振荡之间有产生一相位差。
边界附近的窝度振荡
编辑振荡斯托克斯流解的一大重点是窝度振荡受限于狭小边界层中并在远离平面时以指数衰减。[7]这个发现同样适用于涡流边界层。在斯托克斯边界层外(充满大部分流体的地方),涡流振荡可以被忽略。作为好的近似, 流速振荡在边界层外是无旋的,且位流理论可用来解释振荡运动的部分。这大大简化了问题,也很常被应用在声波和水波的无旋部分。
受制于上平面的流体
编辑若流体受制于位置 ,固定不动的上平面,那么流速可以被写为
其中 。
流体受制于自由平面
编辑假设流体区域为 , 处代表一个自由面。其解在1968 被易家训院士[8] 解出,其为
其中
平面附近受周期压力梯度振荡的流体行为
编辑对于振荡远场流的情况,考虑平面静止, 其可以透过先前的解借由线性叠加原理组合起来。考虑远离平面处波速以 振荡,在平面处 。不像先前稳流情况,这边无限远处的压力梯度会是一个时间的周期函数,其解为
在 z = 0 的地方值为0, 此与平面静止的不滑移条件有关。这个解很常在墙壁附近的声波问题碰到,或是水床附近的水波问题。静止平面附近的窝度振荡值与振荡平面的值相同,但差一负号。
圆柱对称下的斯托克斯问题
编辑扭转振荡
编辑考虑无限长、半径为 的圆柱体以角速度 作扭转振荡, 是其振荡角频率。那么暂态后的速度会趋向于[9]
其中 第二种形式的修正 Bessel Function。这个解可以被表示为下式的实数部分: [10]
其中
和 是开尔文函数, 是无单位的振荡雷诺数,定义为 ,其中 是运动黏度。
轴向振荡
编辑若圆柱体在轴向以 振荡,其速度场为
其中 为修正Bessel Function的第二种形式。
对于泰勒-库埃特流,除了其中一个平面的平移运动, 其平面的周期运动是可以被运算的。若我们有个在 的静止平面与在 的上表面,受 的速度振荡驱动, 其速度场可被写为
单位面积施加在移动平面上的摩擦力为 ,施加在静止的则是 。
其他相关
编辑参考资料
编辑- ^ Wang, C. Y. Exact solutions of the steady-state Navier-Stokes equations. Annual Review of Fluid Mechanics. 1991, 23: 159–177. Bibcode:1991AnRFM..23..159W. doi:10.1146/annurev.fl.23.010191.001111.
- ^ Landau & Lifshitz (1987), pp. 83–85.
- ^ Batchelor, George Keith. An introduction to fluid dynamics. Cambridge university press, 2000.
- ^ Lagerstrom, Paco Axel. Laminar flow theory. Princeton University Press, 1996.
- ^ Acheson, David J. Elementary fluid dynamics. Oxford University Press, 1990.
- ^ Landau, Lev Davidovich, and Evgenii Mikhailovich Lifshitz. "Fluid mechanics." (1987).
- ^ Phillips (1977), p. 46.
- ^ Yih, C. S. (1968). Instability of unsteady flows or configurations Part 1. Instability of a horizontal liquid layer on an oscillating plane. Journal of Fluid Mechanics, 31(4), 737-751.
- ^ Drazin, Philip G., and Norman Riley. The Navier–Stokes equations: a classification of flows and exact solutions. No. 334. Cambridge University Press, 2006.
- ^ Rivero, M.; Garzón, F.; Núñez, J.; Figueroa, A. Study of the flow induced by circular cylinder performing torsional oscillation. European Journal of Mechanics - B/Fluids. 2019, 78: 245–251. S2CID 201253195. doi:10.1016/j.euromechflu.2019.08.002 (英语).
- ^ Landau, L. D., & Sykes, J. B. (1987). Fluid Mechanics: Vol 6. pp. 88