应力集中

应力集中是应力在物体中的局部产生显著升高的现象。在物体中的几何不连续（不平滑）导致了局部应力场强度的提升。最大应力往往超过屈服极限使应力的重新分配，所以实际的最大应力常低于弹性力学计算出的理论峰值。

圆孔周围的力流动（红色曲线）与流场中的流线类似。 曲线之间的间距在孔侧是最小的，反映了应力集中。

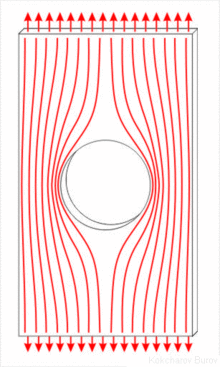
应力集中的发生

1.几何不连续性。

2.施加载荷的不连续性。

3.材料的不连续性。

研究进程

1898年，E.G Kirsch 首先发现圆形缺孔附近有应力集中状况。1913年，C.E. Inglis 计算出椭圆形附近的应力集中，为线弹性断裂力学理论跨出新的一步。 1920年，A. A. Griffith 进一步基于能量的分析，开创了断裂力学的领域。应力集中由许多因子所组成，1953年，Peterson首次出版"Stress Concentration Design Factors"，为设计阶段提供估算应力集中系数的方法。