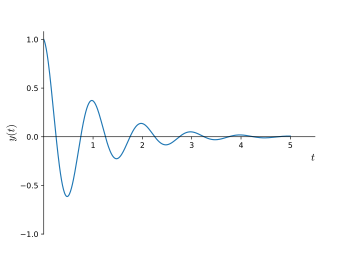
阻尼正弦波
阻尼正弦波(英语:damped sine wave)是振幅会随时间增长而趋向零的正弦波函数[1]。
定义
编辑许多振动的现象可以用正弦波来描述,若振动系统中有阻尼,其振幅会随著时间而减少。
真正的正弦波在时间为0时从原点开始(振幅为0),馀弦波和正弦波有相位差,在原点时有最大值。在实务上的弦波可能具有正弦及馀弦的份,因此“阻尼正弦波”也包括这些不同相位的弦波在有阻尼时的波形。
方程
编辑指数衰减的弦波其方程如下:
其中
- 为时间t的瞬时值
- 为包络线的初始值
- 为递减常数,其单位是X轴时间的倒数
- 是特定点的相位角
- 是角频率
可以简化为
其中:
- 为t = 0的相位角
其他重要的参数有:
相关条目
编辑参考资料
编辑- ^ Douglas C. Giancoli (2000). [Physics for Scientists and Engineers with Modern Physics (3rd Edition)]. Prentice Hall. ISBN 0-13-021517-1
