雙倒數圖
雙倒數圖也稱為萊恩威弗-伯克作圖，是生物化學用來描述酶動力學的萊恩威弗-伯克方程的圖示法，由漢斯·萊恩威弗和迪恩·伯克於1934年提出[1]。
推導
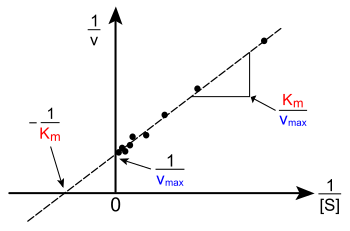
編輯雙倒數圖被用來圖像分析米氏方程：
![{\displaystyle V={\frac {V_{\max }[S]}{K_{m}+[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fa5b35e10661c7592ae5bc59429f1033a4acbf8)
取倒數得到
![{\displaystyle {1 \over V}={{K_{m}+[S]} \over V_{\max }[S]}={K_{m} \over V_{\max }}{1 \over [S]}+{1 \over V_{\max }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/262e1440a8ad30a692b153178eabbf6e7f45d48f)
其中
應用
編輯在強大的計算機和非線性回歸軟件出現前雙倒數圖被廣泛用來確定酶動力學裡的項，比如Km和Vmax。雙倒數圖的截距等於Vmax的逆數。雙倒數圖的根等於−1/Km。雙倒數圖還能很快地體現不同形式的酶抑制。
雙倒數圖扭曲數據結構，因此它不能可靠地確定酶動力學係數。雖然今天它依然被用來顯示動力學數據[2]，一般米氏動力學的非線性回歸圖象或者其它線性圖象如哈尼斯-伍爾夫圖或伊迪-霍夫斯蒂圖被用來計算係數[3]。
雙倒數圖可以用來區別競爭性抑制、非競爭性抑制和不競爭性抑制。競爭性抑制劑和不競爭性抑制劑的y截距相同，但是傾斜度不同，x也不同。非競爭性抑制劑和不競爭性抑制劑的x截距相同，但是傾斜度不同，因此y不同。競爭性抑制劑和非競爭性抑制劑的y和x都不同。
缺點
編輯在較舊的書籍裡雙倒數圖經常被使用，但是它很容易出錯誤。它的y軸是反應速度的倒數，因此小的測量錯誤會被放大。此外大多數圖在y軸的右邊很遠的地方，因此要通過很大的外推來獲得x和y的截距[4]。
參考資料
編輯- ^ Lineweaver, H and Burk, D. The Determination of Enzyme Dissociation Constants. Journal of the American Chemical Society. 1934, 56 (3): 658–666. doi:10.1021/ja01318a036.
- ^ Hayakawa, K.; Guo, L.; Terentyeva, E.A.; Li, X.K.; Kimura, H.; Hirano, M.; Yoshikawa, K.; Nagamine, T.; et al. Determination of specific activities and kinetic constants of biotinidase and lipoamidase in LEW rat and Lactobacillus casei (Shirota). J Chromatogr B Analyt Technol Biomed Life Sci. 2006, 844 (2): 240–50. PMID 16876490. doi:10.1016/j.jchromb.2006.07.006.
- ^ Greco, W. R. and Hakala, M. T.,. Evaluation of methods for estimating the dissociation constant of tight binding enzyme inhibitors, (PDF). J. Biol. Chem. 1979, 254 (23): 12104–12109 [2015-11-21]. PMID 500698. （原始內容 (PDF)存檔於2009-03-20）.
- ^ Dowd, John E.; Riggs, Douglas S. A Comparison of Estimates of Michaelis–Menten Kinetic Constants from Various Linear Transformations. J. Biol. Chem. 1965, 240 (2): 863–869 [2015-11-21]. （原始內容存檔於2015-01-22）.