雙曲樹
雙曲樹(英語:hyperbolic tree)是一種信息可視化和圖形繪製方法,其靈感來自雙曲幾何。

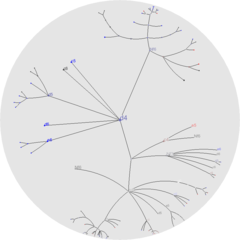
將分層數據顯示為一棵樹,由於每層的節點數量會呈指數級增長,因此會出現視覺上的混亂。對於一棵簡單的二叉樹來說,第 n 層的最大節點數是 2n,而分支較多的樹的節點數增長得更快。因此,把樹畫成一個節點-鏈接圖需要指數級的空間來顯示。
解決上述問題的其中一種方法是使用雙曲樹,首先由Lamping等人提出。[1] 雙曲樹採用雙曲空間,其本質上比歐氏空間的「空間更大」。例如,在歐幾里得空間中線性增加一個圓的半徑,其周長會線性增加,而在雙曲空間中同樣的圓,其周長會呈指數級增加。利用這一特性,可以在雙曲空間中以整潔的方式給樹布局:把一個節點放在離其父節點足夠遠的地方,可以讓該節點幾乎擁有與其父節點相同的空間來布局自己的子節點。
通常利用雙曲幾何的龐加萊圓盤模型來展示雙曲樹,儘管也可以使用凱萊-克萊因模型。兩者都是在一個單位圓盤中顯示整個雙曲平面,使整個樹一次性可見。單位圓盤提供了一個平面的魚眼透鏡視圖,更加強調焦點內的節點,而在靠近圓盤邊界處可以顯示更加遠離焦點的節點。遍歷雙曲樹需要對空間進行莫比烏斯變換,使新的節點成為焦點,並將層次結構的更高層次移出視野。
雙曲樹於1996年由施樂公司在美國申請了專利,但該專利已經過期。[2]
參見
編輯參考文獻
編輯- ^ Lamping, John Ogden; Rao, Ramana; Pirolli, Peter. A focus+context technique based on hyperbolic geometry for visualizing large hierarchies. Proceedings of the ACM Conference on Human Factors in Computing Systems (CHI 1995): 401–408. May 1995 [2021-04-13]. doi:10.1145/223904.223956. (原始內容存檔於2017-05-10).
- ^ US patent 5590250,Lamping; John O. & Rao; Ramana B.,「Layout of node-link structures in space with negative curvature」,指定於Xerox Corporation
外部連結
編輯- d3-hypertree (頁面存檔備份,存於網際網路檔案館) – HTML5 Hyperbolic tree implementation, MIT licensed
- Hyperbolic Tree of life (頁面存檔備份,存於網際網路檔案館) – Open source tree of life visualisation using Open Tree of Life data set
- The Green Tree of Life (頁面存檔備份,存於網際網路檔案館) – Tree of life – University of California at Berkeley and Jepson Herbaria
- Tree of life Similar to the above, but with pictures
- RougeViz (頁面存檔備份,存於網際網路檔案館) supports hyperbolic trees.