三角形分佈

在機率論與統計學中，三角形分佈是低限為 a、眾數為 c、上限為 b 的連續機率分佈。

三角形分佈

機率密度函數
累積分佈函數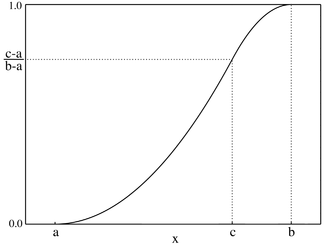
參數	$a:~a\in (-\infty ,\infty )$ $b:~b>a\,$ $c:~a\leq c\leq b\,$
值域	$a\leq x\leq b\!$
機率密度函數	$\left\{{\begin{matrix}{\frac {2(x-a)}{(b-a)(c-a)}}&\mathrm {for\ } a\leq x\leq c\\&\\{\frac {2(b-x)}{(b-a)(b-c)}}&\mathrm {for\ } c<x\leq b\end{matrix}}\right.$
累積分佈函數	$\left\{{\begin{matrix}{\frac {(x-a)^{2}}{(b-a)(c-a)}}&\mathrm {for\ } a\leq x\leq c\\&\\1-{\frac {(b-x)^{2}}{(b-a)(b-c)}}&\mathrm {for\ } c<x\leq b\end{matrix}}\right.$
期望值	${\frac {a+b+c}{3}}$
中位數	$\left\{{\begin{matrix}a+{\frac {\sqrt {(b-a)(c-a)}}{\sqrt {2}}}&\mathrm {for\ } c\!\geq \!{\frac {b\!-\!a}{2}}\\&\\b-{\frac {\sqrt {(b-a)(b-c)}}{\sqrt {2}}}&\mathrm {for\ } c\!\leq \!{\frac {b\!-\!a}{2}}\end{matrix}}\right.$
眾數	$c\,$
變異數	${\frac {a^{2}+b^{2}+c^{2}-ab-ac-bc}{18}}$
偏度	${\frac {{\sqrt {2}}(a\!+\!b\!-\!2c)(2a\!-\!b\!-\!c)(a\!-\!2b\!+\!c)}{5(a^{2}\!+\!b^{2}\!+\!c^{2}\!-\!ab\!-\!ac\!-\!bc)^{\frac {3}{2}}}}$
峰度	${\frac {12}{5}}$
熵	${\frac {1}{2}}+\ln \left({\frac {b-a}{2}}\right)$
動差母函數	$2{\frac {(b\!-\!c)e^{at}\!-\!(b\!-\!a)e^{ct}\!+\!(c\!-\!a)e^{bt}}{(b-a)(c-a)(b-c)t^{2}}}$
特徵函數	$-2{\frac {(b\!-\!c)e^{iat}\!-\!(b\!-\!a)e^{ict}\!+\!(c\!-\!a)e^{ibt}}{(b-a)(c-a)(b-c)t^{2}}}$

$f(x|a,b,c)=\left\{{\begin{matrix}{\frac {2(x-a)}{(b-a)(c-a)}}&\mathrm {for\ } a\leq x\leq c\\&\\{\frac {2(b-x)}{(b-a)(b-c)}}&\mathrm {for\ } c<x\leq b\end{matrix}}\right.$

特例

已知兩點

當 c=a 或者 c=b，分佈就可以進行簡化。例如，如果 a=0、b=1 並且 c=1，那麼上面的方程簡化為：

$\left.{\begin{matrix}f(x)&=&2x\\\\F(x)&=&x^{2}\end{matrix}}\right\}\mathrm {for\ } 0\leq x\leq 1$

${\begin{matrix}E(X)&=&{\frac {2}{3}}\\&&\\\mathrm {Var} (X)&=&{\frac {1}{18}}\end{matrix}}$

兩個標準一致變量的分佈

a=0、b=1 且 c=0.5 的分佈為 $X={\frac {X_{1}+X_{2}}{2}}$，其中 $X_{1},X_{2}$ 是兩個連續型均勻分佈的隨機變量。

$f(x)=\left\{{\begin{matrix}4x&\mathrm {for\ } 0\leq x<{\frac {1}{2}}\\\\4-4x&\mathrm {for\ } {\frac {1}{2}}\leq x\leq 1\end{matrix}}\right.$

$F(x)=\left\{{\begin{matrix}2x^{2}&\mathrm {for\ } 0\leq x<{\frac {1}{2}}\\\\1-2(1-x)^{2}&\mathrm {for\ } {\frac {1}{2}}\leq x\leq 1\end{matrix}}\right.$

${\begin{matrix}E(X)&=&{\frac {1}{2}}\\\\\mathrm {Var} (X)&=&{\frac {1}{24}}\end{matrix}}$

三角形分佈的應用

三角形分佈通常用於表述只有有限採樣數據的人口資訊，尤其是已知變量之間的關係但是由於數據的收集成本太高而缺少採樣數據的場合。 這通常是根據已知最小值與最大值從而推算合理的常見值。

商務模擬

三角形分佈經常用於商務決策，尤其是計算機模擬領域。通常，如果對結果的機率分佈所知資訊很少，例如僅僅知道最大值與最小值，那麼可以使用平均分佈模型。但是，如果已經知道了最可能出現的結果，那麼就可以用三角形分佈進行模擬。

項目管理

三角形分佈以及Beta分佈在項目管理中大量地用作項目評估與審核技術以及關鍵途徑的輸入資訊，以建立在最大值與最小值之間事件發生的機率模型。

外部連結與參考文獻

• 三角形分佈（頁面存檔備份，存於互聯網檔案館），mathworld.wolfram.com
• 三角形分佈，decisionsciences.org
• 三角形分佈，brighton-webs.co.uk