斐索實驗
斐索實驗,也譯菲佐實驗[1],是阿爾芒·斐索1851年進行的一項實驗。他在本實驗中測定了光在運動的水中的相對速度。為了確定介質運動對光速的影響,斐索使用了一台特製的干涉儀。
基於當時盛行的理論,在運動介質中傳播的光會被介質拖動,導致最終測到的光速是光和介質的相對速度與介質運動速度的和。雖然斐索在實驗中探測到了拖曳效應,但該效應卻比預期弱很多。他的結果在當時被看作是奧古斯丁·菲涅耳的「以太部分拖曳假說」 的證據,但直到半個多世紀後才通過阿爾伯特·愛因斯坦發展的狹義相對論得到完滿的解釋。愛因斯坦本人認為該實驗對於狹義相對論非常重要。
實驗裝置
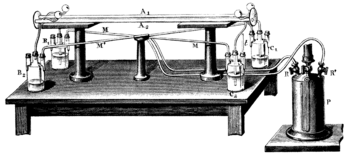
編輯從光源S′放出的光線在被分光鏡G反射後經透鏡L準直為兩束平行光。兩束光線在通過狹縫O1和 O2後進入管道A1和A2。兩個管道分別按照箭頭所指的方向通入水流。在透鏡L′焦點處放置的平面鏡m是為了確保兩束光中有一束總順着水流方向傳播,而另一束則逆着水流傳播。在通過水管後,兩束光線會在S處會聚形成干涉條紋。干涉條紋可以用來分析水管中的光速。[P 1][P 2][S 1]
菲涅耳拖曳係數
編輯假設管中水流速度為v。依據非相對論性理論,光速在以太被水「拖曳」時增大,而在以太「克服」水阻力時減小。總光速是光與水的相對速度與水速的和。
當n是水的折射率時,靜水中的光速會是c/n。那麼上述實驗中,沿着水流方向傳播的光的速度是
逆着水流方向傳播的光的速度則會是
也就是說逆着水流傳播的光會比順着水流傳播的光速度慢。
觀察者看到的兩束光重新會聚形成的干涉條紋取決於兩束光的光程差。它可以用來確定光速與水速之間的函數關係。[S 2]
斐索發現
也就是說,光確實受到水的拖曳效應的影響,但拖曳效應卻比預期弱很多。
斐索實驗令物理學家接受了奧古斯丁·菲涅耳1818年提出的以太部分拖曳理論。菲涅耳曾利用此理論解釋弗朗索瓦·阿拉戈1810年做的一項的實驗的結果。依據這種理論,光速由介質拖曳效應產生的增加量只是介質速度的一部分,拖曳係數f滿足
1895年,亨德里克·勞侖茲又在其中加入了與色散有關的項:[S 3]:15–20
重複實驗
編輯阿爾伯特·邁克生與愛德華·莫雷1886年重複了斐索的實驗,並提升了精度。他們認為斐索的原始實驗存在以下問題:[P 3]
- 儀器變形會導致干涉條紋失真;
- 由於加壓水流持續時間很短,觀察時間非常有限;
- 層流效應導致只有水流最中心部分的流速符合要求,這會導致條紋模糊;
- 斐索測定的水速也存在不確定度。
邁克生重新設計了實驗儀器。他加大了管徑並使用了一個可以提供三分鐘穩定水流的大水池。他所設計的同光路干涉儀(common path interferometer)可以自動補償光路長度。結構上說,光路與薩尼亞克干涉儀(Sagnac interferometer)中的相同。每條光路上都會產生偶數次反射。[S 4]這種儀器對於一階效應的穩定性非常高,並且對於其中任何組件的移位都不敏感。即使在h處放一個玻璃盤或者在光路中放入一個點燃的火柴也不會使條紋中心發生偏移。邁克生與莫雷利用這種儀器確認了斐索的結果。[P 3]
彼得·塞曼也在1914年到1915年間做了重複實驗。他將邁克生的儀器的規模進一步擴大,並將其儀器直接與阿姆斯特丹的主供水管道相連。塞曼還對波長在4358 Å(紫)到6870 Å(紅)範圍內的單色光也進行了測量,以驗證勞侖茲修改後的係數。[P 4][P 5]1910年,弗朗茨·哈雷斯(Franz Harress)使用了可以旋轉的儀器來確認菲涅耳拖曳係數。不過,他發現數據存在「系統性的偏差」。後來他發現這是由薩尼亞克效應造成的。[S 5]從那時起,許多測量拖曳係數的結果也都伴有薩尼亞克效應的影響。[S 6]比如,使用轉盤與環形激光的實驗[P 6][P 7][P 8][P 9]或者中子干涉實驗。[P 10][P 11][P 12]此外,相關研究人員還發現了垂直於光運動的介質產生的橫向拖曳效應。[P 13][P 14]
赫克實驗
編輯馬丁·赫克也在1868年間接驗證了菲涅耳係數。[P 15][S 7]他所用的實驗裝置與斐索的類似,不過其中一條干涉臂充入的是靜水,另一條則是空氣。在靜止以太中的觀察者看來,地球是運動的,也就是說上述裝置中的水也是運動的。所以兩束傳播方向相反的光的傳播時間為(忽略橫向效應):
|
|
|
在上圖所展示的實驗中,赫克先讓狹縫透過的光經稜鏡P色散,然後經C準直再進入主體裝置。他預測當儀器朝向與以太風平行時,一條迴路中的光會受到以太風的影響相對於另一條迴路發生7/600mm的偏移。當這個偏移是光譜中某些光波長的整數倍時就會產生亮條紋;當偏移是波長半整數倍時就會產生暗條紋。而在儀器朝向與以太風垂直時,赫克預測看到的應是連續譜。而在實際實驗中,無論儀器朝向如何,他卻都沒有看到條紋。赫克原本預測,兩束光的傳播是時間並不相同,因此應該能看到干涉偏移。然而,如果對以太系中的水適用菲涅耳拖曳係數,這種時間差(v/c一階效應)就會消失。赫克在使用不同的裝置時得到的也是零結果。這也就驗證了菲涅耳拖曳係數。(古斯塔夫·哈馬爾也曾進行過類似的實驗。該實驗否定了以太風存在的可能性。)[P 15][S 7]
爭議
編輯儘管菲涅耳假說可以解釋斐索的實驗結果,但在這個領域的專家看來,包括斐索本人(1851)、埃勒泰爾·馬斯卡爾(1872)、克特勒(1873)、費爾特曼(1873)以及勞侖茲(1886),菲涅耳的以太部分拖曳假說並不可靠。比如,費爾特曼1870年提出對於不同波長的光,對應的拖曳係數並不相同,因為不同色光的折射率不同。馬斯卡爾則在1872年測定雙折射介質中偏振光的情況時也得到了類似結果。換言之,以太要同時有兩種不同的拖曳係數。[S 8]
斐索本人在實驗報告的結論中也表達了不滿:
實驗的成功讓我不得不接受菲涅耳的假說,或者至少是他找到的動體對於光速的效應。儘管這個已經得到證實的定律可能是假說非常強的證據(儘管這個定律只是其中一個結果)。菲涅耳提出的概念儘管看起來如此接觸,但在部分方面仍然非常難以讓人信服。因此在將其視為真理前仍需要其他證據以及幾何部分的驗證。[P 1]
儘管這些物理學家都對菲涅耳的以太部分拖曳假說表示不滿,但這種假說還是得到了其他科學家在更高精度下的驗證。(見上文)
以太部分拖曳假說除了本身有問題之外,還與邁克生-莫雷實驗(1887)的結果並不兼容。在菲涅耳的假說里,以太幾乎絕對靜止,所以通過米高孫-莫雷實驗應該能得到以太存在的證據。但米高孫-莫雷實驗的結果表明絕對靜止的以太不可能存在。從以太模型的角度來說,當時的實驗結果之間存在很大的分野:一方面,光行差、斐索實驗以及後續重複實驗支持「以太部分拖曳模型」;另一方面,邁克生-莫雷實驗則支持以太相對於地球完全靜止的「完全以太拖曳模型」。[S 9]由此引起的理論危機直到狹義相對論出現後才得到解決。[S 8]
勞侖茲的解釋
編輯1892年,亨德里克·勞侖茲對於菲涅耳的模型做了修正。在他的模型中,以太是完全靜止的。勞侖茲利用水與靜止以太之間的相互作用推出了菲涅耳拖曳係數。[S 9][S 10]:25–30他還發現可以通過引入時間參量,「局部時」,來簡化參考系之間的變換:
1895年,勞侖茲基於局部時的概念給出了菲涅耳係數更為普遍的解釋。然而,勞侖茲的理論與菲涅耳的理論具有相同的基礎問題,即不能與邁克生-莫雷實驗的結果相調和。所以勞侖茲在1892年提出了運動物體會在運動方向上發生長度收縮的假說(喬治·斐茲傑惹也在1889年提出類似假說)。他後來又繼續發展能夠描述這些效應的方程式。最終的方程組後來叫做「勞侖茲變換」。這個方程組與愛因斯坦後來從第一性原理推得的方程組形式相同。但與愛因斯坦的方程組不同的是,勞侖茲的方程組只是特例假設,也就是說它們只是為了使已有的理論成立才設立的。[S 9][S 10]:27–30
狹義相對論解釋
編輯愛因斯坦後來展示了勞侖茲的方程組如何從狹義相對論的兩條公設推出。除此之外,愛因斯坦還認定靜止以太在狹義相對論中沒有存在的必要,並且勞侖茲變換與時空本身性質有關。與移動中的磁鐵與導體問題、以太零漂移實驗以及光行差問題一樣,斐索實驗是促成愛因斯坦形成相對性思想的關鍵實驗結果之一。[S 11][S 12]羅拔·尚克蘭與愛因斯坦曾經有過幾次交流。愛因斯坦是這樣強調斐索實驗的重要性的:[S 13]
他接着說道,對他影響最大的實驗結果是天體光行差的觀測以及斐索對於流動的水中光速的測定。「有它們就足夠了。」他這樣說。
馬克斯·馮·勞厄在1907年展示了菲涅耳拖曳係數可以通過相對論中的速度加成式推出:[S 14]
- 靜水中的光速為c/n
- 從速度加成式可以得到,實驗室中觀測到的流速為v的水流中光速(光的傳播方向與水流方向一致)為
- 因此速度差為(假設v相對於c非常小,可以在高階項中省略)
- 此式在v/c ≪ 1成立,並與斐索得到的方程式一致(斐索實驗滿足v/c ≪ 1)
斐索實驗也因此可以驗證愛因斯坦速度加成式在合成速度共線的情況下成立。[P 16]
參看
編輯參考文獻
編輯- ^ Fizeau. 術語在線. 全國科學技術名詞審定委員會. (簡體中文)
- 第二手來源
- ^ Mascart, Éleuthère Élie Nicolas. Traité d'optique. Paris: Gauthier-Villars. 1889: 101 [9 August 2015].
- ^ Robert Williams Wood. Physical Optics. The Macmillan Company. 1905: 514 [2017-02-23]. (原始內容存檔於2019-05-02).
- ^ Pauli, Wolfgang. Theory of Relativity. New York: Dover. 1981 [1921]. ISBN 0-486-64152-X.
- ^ Hariharan, P. Basics of Interferometry, 2nd edition. Elsevier. 2007: 19. ISBN 0-12-373589-0.
- ^ Anderson, R.; Bilger, H.R.; Stedman, G.E. Sagnac effect: A century of Earth-rotated interferometers. Am. J. Phys. 1994, 62 (11): 975–985. Bibcode:1994AmJPh..62..975A. doi:10.1119/1.17656.
- ^ Stedman, G. E. Ring-laser tests of fundamental physics and geophysics. Reports on Progress in Physics. 1997, 60 (6): 615–688. Bibcode:1997RPPh...60..615S. doi:10.1088/0034-4885/60/6/001.; see pp. 631–634, and references therein.
- ^ 7.0 7.1 Rafael Ferraro. Hoek's experiment. Einstein's Space-Time: An Introduction to Special and General Relativity. Springer. 2007: 33–35. ISBN 0-387-69946-5.
- ^ 8.0 8.1 Stachel, J. Fresnel's (dragging) coefficient as a challenge to 19th century optics of moving bodies. Kox, A.J.; Eisenstaedt, J (編). The universe of general relativity. Boston: Birkhäuser. 2005: 1–13 [17 April 2012]. ISBN 0-8176-4380-X.
- ^ 9.0 9.1 9.2 Janssen, Michel; Stachel, John, The Optics and Electrodynamics of Moving Bodies (PDF), John Stachel (編), Going Critical, Springer, 2010 [2012-04-23], ISBN 1-4020-1308-6, (原始內容存檔 (PDF)於2015-09-29)
- ^ 10.0 10.1 Miller, A.I. Albert Einstein's special theory of relativity. Emergence (1905) and early interpretation (1905–1911). Reading: Addison–Wesley. 1981. ISBN 0-201-04679-2.
- ^ Lahaye, Thierry; Labastie, Pierre; Mathevet, Renaud. Fizeau's "aether-drag" experiment in the undergraduate laboratory. American Journal of Physics. 2012, 80 (6): 497. Bibcode:2012AmJPh..80..497L. arXiv:1201.0501 . doi:10.1119/1.3690117.
- ^ Norton, John D., John D., Einstein's Investigations of Galilean Covariant Electrodynamics prior to 1905, Archive for History of Exact Sciences, 2004, 59: 45–105 [2017-02-23], Bibcode:2004AHES...59...45N, doi:10.1007/s00407-004-0085-6, (原始內容存檔於2009-01-11)
- ^ Shankland, R. S. Conversations with Albert Einstein. American Journal of Physics. 1963, 31 (1): 47–57. Bibcode:1963AmJPh..31...47S. doi:10.1119/1.1969236.
- ^ N David Mermin. It's about time: understanding Einstein's relativity. Princeton University Press. 2005: 39 ff [2017-02-23]. ISBN 0-691-12201-6. (原始內容存檔於2019-05-02).
- 第一手來源
- ^ 1.0 1.1 Fizeau, H. Sur les hypothèses relatives à l'éther lumineux. Comptes Rendus. 1851, 33: 349–355 [2017-02-23]. (原始內容存檔於2011-12-30).
- English: Fizeau, H. The Hypotheses Relating to the Luminous Aether, and an Experiment which Appears to Demonstrate that the Motion of Bodies Alters the Velocity with which Light Propagates itself in their Interior. Philosophical Magazine. 1851, 2: 568–573.
- ^ Fizeau, H. Sur les hypothèses relatives à l'éther lumineux. Ann. Chim. Phys. 1859, 57: 385–404 [2017-02-23]. (原始內容存檔於2020-11-24).
- English: Fizeau, H. On the Effect of the Motion of a Body upon the Velocity with which it is traversed by Light. Philosophical Magazine. 1860, 19: 245–260.
- ^ 3.0 3.1 Michelson, A. A.; Morley, E.W. Influence of Motion of the Medium on the Velocity of Light. Am. J. Sci. 1886, 31: 377–386.
- ^ Zeeman, Pieter. Fresnel's coefficient for light of different colours. (First part). Proc. Kon. Acad. Van Weten. 1914, 17: 445–451. Bibcode:1914KNAB...17..445Z.
- ^ Zeeman, Pieter. Fresnel's coefficient for light of different colours. (Second part). Proc. Kon. Acad. Van Weten. 1915, 18: 398–408. Bibcode:1915KNAB...18..398Z.
- ^ Macek, W. M. Measurement of Fresnel Drag with the Ring Laser. Journal of Applied Physics. 1964, 35 (8): 2556–2557. Bibcode:1964JAP....35.2556M. doi:10.1063/1.1702908.
- ^ Bilger, H. R.; Zavodny, A. T. Fresnel Drag in a Ring Laser: Measurement of the Dispersive Term. Physical Review A. 1972, 5 (2): 591–599. Bibcode:1972PhRvA...5..591B. doi:10.1103/PhysRevA.5.591.
- ^ Bilger, H. R.; Stowell, W. K. Light drag in a ring laser – An improved determination of the drag coefficient. Physical Review A. 1977, 16: 313–319. Bibcode:1977PhRvA..16..313B. doi:10.1103/PhysRevA.16.313.
- ^ Sanders, G. A.; Ezekiel, Shaoul. Measurement of Fresnel drag in moving media using a ring-resonator technique. Journal of the Optical Society of America B. 1988, 5 (3): 674–678. Bibcode:1988JOSAB...5..674S. doi:10.1364/JOSAB.5.000674.
- ^ Klein, A. G.; Opat, G. I.; Cimmino, A.; Zeilinger, A.; Treimer, W.; Gähler, R. Neutron Propagation in Moving Matter: The Fizeau Experiment with Massive Particles. Physical Review Letters. 1981, 46 (24): 1551–1554. Bibcode:1981PhRvL..46.1551K. doi:10.1103/PhysRevLett.46.1551.
- ^ Bonse, U.; Rumpf, A. Interferometric measurement of neutron Fizeau effect. Physical Review Letters. 1986, 56 (23): 2441–2444. Bibcode:1986PhRvL..56.2441B. PMID 10032993. doi:10.1103/PhysRevLett.56.2441.
- ^ Arif, M.; Kaiser, H.; Clothier, R.; Werner, S. A.; Hamilton, W. A.; Cimmino, A.; Klein, A. G. Observation of a motion-induced phase shift of neutron de Broglie waves passing through matter near a nuclear resonance. Physical Review A. 1989, 39 (3): 931–937. Bibcode:1989PhRvA..39..931A. PMID 9901325. doi:10.1103/PhysRevA.39.931.
- ^ Jones, R. V. 'Fresnel Aether Drag' in a Transversely Moving Medium. Proceedings of the Royal Society A. 1972, 328 (1574): 337–352. Bibcode:1972RSPSA.328..337J. doi:10.1098/rspa.1972.0081.
- ^ Jones, R. V. "Aether Drag" in a Transversely Moving Medium. Proceedings of the Royal Society A. 1975, 345 (1642): 351–364. Bibcode:1975RSPSA.345..351J. doi:10.1098/rspa.1975.0141.
- ^ 15.0 15.1 Hoek, M. Determination de la vitesse avec laquelle est entrainée une onde lumineuse traversant un milieu en mouvement. Verslagen en mededeelingen. 1868, 2: 189–194.
- ^ Laue, Max von, Die Mitführung des Lichtes durch bewegte Körper nach dem Relativitätsprinzip [The Entrainment of Light by Moving Bodies in Accordance with the Principle of Relativity], Annalen der Physik, 1907, 328 (10): 989–990, Bibcode:1907AnP...328..989L, doi:10.1002/andp.19073281015