月角距
月角距是月球和另一個天體之間的角度,是在天文導航中使用的術語。領航員可以利用月角距 (也稱為月球) 和航海年曆計算格林威治時間。然後,領航員不需要航海鐘就可以確定經度。
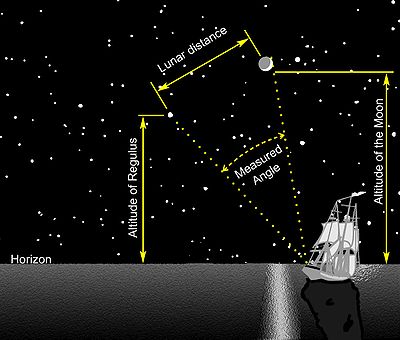
測量月角距的原因
編輯在天文導航,精確的知道格林威治時間和結合仔細觀察一個或多個天體的位置,可以計算經度和緯度[1]。直到18世紀後期才有可靠的航海鐘可以使用,而直到19世紀初期才負擔得起費用[2][3][4]。大約有一百多年 (大約從1767年直到1850年)[5],缺乏天文鐘的水手使用月角距法測量格林威治時間,是查找其經度的重要步驟。有天文鐘的水手可以使用月角距得到的讀數檢查和校正格林威治時間[2]。
方法
編輯摘要
編輯這種方法依賴月球在背景天空中相對快速的運動,其只需要27.3天就移動一圈,即一個恆星月。一小時內它將相對於背景恆星或太陽移動大約半度[1],大致為它的直徑。而通過使用六分儀,領航員可以精確的測量月球和其它天體之間的夾角[1],這可以是太陽,也可以是靠近月球路徑、靠近黃道的一組特定明亮恆星中的一顆。在同一時刻,地球表面上任何能夠看到相同的兩個天體的人在校正視差後,都會觀察到相同的角度。因此,領航員通過查閱事前準備好的月球距離與它們會發生的時間表[1][6],經過比較表單上的數值和修正月角距,領航員可以算出觀測時的格林威治時間。知道格林威治時間和當地時間,領航員就可以推導出當地的經度[1];使用六分儀觀察太陽或一顆恆星的高度,可以測量出地方時[7][8]。然後,就可以由格林威治時間和本地時間的差異(每小時15度)來計算出經度。
實務
編輯測量月角距和這兩個天體的高度,領航員可以經由下面三個步驟得到格林威治時間。
- 第一步 - 準備
- 預測月球中心和其它天體距離的月角距年曆表 (從1767年到1900年,可以在任何一本航海年曆上找到)[來源請求]。不過,觀測者不容易精確的找出月球的中心 (和太陽,它是第二個最常用到的天體)。取而代之的是,月角距經常是測量明顯的亮緣,月球的外緣和明確可見的太陽邊緣。月球距離的第一個修正值是月球邊緣與中心的距離。由於月球的視大小隨着與地球的距離而改變,年曆會給出太陽和月球每一天的半徑 (請參閱該年度的航海年曆)。另外,觀測到的高度被消除了半徑和傾角。
- 第二步 - 清算
- 清算月角距是指修正視差和大氣折射在觀測上造成的影響。年曆上給的月角距是觀測者位於一個透明地球的中心所看見的。因為月球遠比其它的恆星更接近地球,在地球表面的觀測者看見的月球相對位置可以相差到一整度[9][10]。清算和校正視差和大氣折射,相較於觀測月角距和天體高度這兩者,只是簡單的三角函數計算[11]。領航員可以從蒐集到的任何一種數學表,使用數十種不同的計算方法來完成工作。
找出了 (絕對的) 格林威治時間,領航員要不是比較觀測位置的地方時間 (一個單獨的觀測) 來發現經度,或是,如果可以,與航海鐘的格林威治時間比較[1]。
誤差
編輯- 月角距誤差對經度計算的影響
- 月角距相對於時間的變化率大約是每小時半度,或30弧分[1],因此,每半弧分的誤差會使格林威治時間偏差約一分鐘,這相當於在經度上差了四分之一度 (由於地球每小時轉15度,在赤道大約相當於15海浬)。
- 年表誤差
- 月角距在早期,最好的月球位置預測偏差大約是半弧分,在時間源頭的格林威治時間上造成約1分鐘的誤差,或是經度上四分之一度的誤差。在1810年,年表上預報的誤差減小至四分之一弧分;大約在1850年 (月角距的觀測大多已成為歷史之後),年表上的誤差已經小於六分儀在理想條件下的誤差 (十分之一弧分)。
- 月角距觀測
- 在剛開始觀測月球距離的時期,最好的六分儀可以標示出六分之一弧分的角度,稍後,六分儀的精確度提升到0.1弧分。在海上的實務,誤差會較大些。經驗豐富的觀測者,在良好的條件下,對月角距的測量可以準確至四分之一弧分,使引入的誤差在經度上只有四分之一度。不用說,如果是多雲的天空或是"新月" (隱藏或靠近耀眼的陽光),就不能執行月角距的觀察。
- 總誤差
- 上述兩種來源的誤差,結合在一起,通常會造成月角距半弧分的誤差,相當於格林威治時間的一分鐘,等同於在經度上四分之一度的偏差,在赤道上大約是15海里(30公里)的距離。
文學
編輯此條目需要擴充。 (2011年11月30日) |
相關條目
編輯參考資料
編輯- ^ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Norie, J. W. New and Complete Epitome of Practical Navigation. London. 1828: 222 [2007-08-02]. (原始內容存檔於2007-09-27).
- ^ 2.0 2.1 Norie, J. W. New and Complete Epitome of Practical Navigation. London. 1828: 221 [2007-08-02]. (原始內容存檔於2007-09-27).
- ^ Taylor, Janet. An Epitome of Navigation and Nautical Astronomy Ninth. 1851: 295f [2007-08-02]. (原始內容存檔於2020-03-03).
- ^ Britten, Frederick James. Former Clock & Watchmakers and Their Work. New York: Spon & Chamberlain. 1894: 230 [2007-08-08]. (原始內容存檔於2020-06-27).
Chronometers were not regularly supplied to the Royal Navy till about 1825
- ^ Lecky, Squire, Wrinkles in Practical Navigation
- ^ 6.0 6.1
Royal Greenwich Observatory. DISTANCES of Moon's Center from Sun, and from Stars EAST of her. Garnet (編). The Nautical Almanac and Astronomical Ephemeris for the year 1804. Second American Impression. New Jersey: Blauvelt. : 92 [2007-08-02]. (原始內容存檔於2007-09-27).;
Wepster, Steven. Precomputed Lunar Distances. [2007-08-02]. (原始內容存檔於2007-12-15). - ^ Norie, J. W. New and Complete Epitome of Practical Navigation. London. 1828: 226 [2007-08-02]. (原始內容存檔於2007-09-27).
- ^ Norie, J. W. New and Complete Epitome of Practical Navigation. London. 1828: 230 [2007-08-02]. (原始內容存檔於2007-09-27).
- ^ Duffett-Smith, Peter. Practical Astronomy with Your Calculator, third edition. 1988: 66 [2021-12-26]. (原始內容存檔於2016-05-10).
- ^ Montenbruck and Pfleger. Astronomy on the Personal Computer, second edition. 1994: 45–46 [2021-12-26]. (原始內容存檔於2016-05-26).
- ^ Schlyter, Paul. The Moon's topocentric position. [2011-07-18]. (原始內容存檔於2021-03-22).
- New and complete epitome of practical navigation containing all necessary instruction for keeping a ship's reckoning at sea ... to which is added a new and correct set of tables - by J. W. Norie 1828
- Andrewes, William J.H. (Ed.): The Quest for Longitude. Cambridge, Mass. 1996
- Forbes, Eric G.: The Birth of Navigational Science. London 1974
- Jullien, Vincent (Ed.): Le calcul des longitudes: un enjeu pour les mathématiques, l`astronomie, la mesure du temps et la navigation. Rennes 2002
- Howse, Derek: Greenwich Time and the Longitude. London 1997
- Howse, Derek: Nevil Maskelyne. The Seaman's Astronomer. Cambridge 1989
- National Maritime Museum (Ed.): 4 Steps to Longitude. London 1962
外部連結
編輯- The lunar distance page
- About Lunars... by George Huxtable. (Free tutorial)
- Navigation Spreadsheets: Lunar distance (頁面存檔備份,存於互聯網檔案館)
- Navigational Algorithms - free software for Lunars (頁面存檔備份,存於互聯網檔案館)
- Longitude by Lunars online