薄透鏡,在光學中,是指透鏡的厚度(穿過光軸的兩個鏡子表面的距離)與焦距的長度比較時,可以被忽略不計的透鏡。厚度不能被忽略的透鏡稱為厚透鏡。
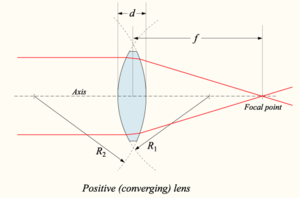 如果d << f,透鏡就可以看成是薄透鏡。
推導薄透鏡公式
如果d << f,透鏡就可以看成是薄透鏡。
推導薄透鏡公式
薄透鏡有兩個球面組成,第一曲面的曲率半徑=R1,第二球面的曲率半徑=R2;在第一球面面左邊的介質(空氣)的折射係數=N1=1,透鏡材料的折射係數=N2,透鏡右邊介質(空氣)的折射係數=N3=1。物距=-L1,像距=L3。
根據球面折射的近軸近似,
第一球面服從下列折射方程
-
第二球面服從下列折射方程
-
兩式相加得:
-
-
對一個薄透鏡,物距( )和像距( )的近軸近似關係式是:
-
[1][2]。
當物距趨向無窮大,即D→∝ →0
上式化為:
- 。
定義 f為 物距在無窮大時的像距 f:= d(當s→∝)
於是
- 。
-
稱為薄透鏡焦距。其中N是薄透鏡的材料折射率,R1,R2是球面的半徑,半徑的方向和光軸相同為正號,反之為負號。
f >0的透鏡稱為凸透鏡,f <0的透鏡稱為凹透鏡。
焦距的倒數 稱為透鏡的焦度,或屈光度,用Φ表示
- 。
所謂近軸近似指光線在透鏡上的入射角i很小,因此折射定律中的正弦sin(i)≈i。當光線的入射角的正弦不可用角度代替時,上述薄透鏡公式不成立。
由薄透鏡公式
- (物距(D)和像距(d)),通分後可得
- 移項後得:
在等式兩邊各加
由此可得薄透鏡的牛頓公式
倍率,又稱「放大率」,是指像高與物高之比。
令M代表倍率:
其中h為像高,H為物高,d為像距,D為物距。
由牛頓公式
代人 得
在微距攝影中,當物高=像高,即M=1時
即物距=像距=鏡頭焦距的2倍。
薄透鏡公式中
- 。
令 c1= 代表透鏡第一球面的曲率
令 c2= 代表透鏡第二球面的曲率
則
其中c =c1-c2代表透鏡的總曲率。
由上式可見,顯然薄透鏡的焦距只和透鏡的總曲率有關;因此,可以改變兩個曲面的曲率,而仍然保持鏡頭的焦距不變:
即
第一曲面的曲率c1增加k,第二曲面的曲率也增加k,鏡頭的總曲率不變,鏡頭的焦距不變。這種同步改變薄透鏡的兩個球面的曲率而維持透鏡焦距的技術,稱為鏡片彎曲術,是鏡頭設計時在保障焦距不變的條件下調控像差的強有力的手段之一[3]。
令 X= [4][5]。
一個薄透鏡,如果第一曲面是球面,第二面是平面,則X=1,如第一面是平面,第二面是球面則X =-1,雙凸透鏡X=0>[4][5]。
兩個同光軸薄透鏡,其焦度分別為 , ,間距為d,
則兩個薄透鏡組和的焦度為[6]
當兩個同光軸薄透鏡十分靠近,d≈0;則組和的焦度為兩透鏡焦度之和:
- ^ A.E.Conrady Applied Optics and Optical Design Section 23 Simple Lens, p60-62,Dover
- ^ Dennis Taylor p9-10
- ^ Conrady, p64
- ^ 4.0 4.1 Kingslake p57
- ^ 5.0 5.1 Kidger p139
- ^ Warren Smith, Modern Lens Design, A Resource Manual, p446 McGraw-Hill, NY, ISBN 0-07-059178-4
- Harold Dennis Taylor, A System of Appied Optics 1906
- Alexander Eugen Conrady Applied Optcs and Optical Design, Dover 1957
- Rudolf Kingslake, Lens Design Fundamentals, Academic Press, New York 1978
- Michael J. Kidger, Fundamental Optical Design 2001 SPIE ISBN 978-0819439154
