圓形圖
圓形圖,或稱餅圖,是一個劃分為幾個扇形的圓形統計圖表,用於描述量、頻率或百分比之間的相對關係。在圓形圖中,每個扇區的弧長(以及圓心角和面積)大小為其所表示的數量的比例。這些扇區合在一起剛好是一個完全的圓形。顧名思義,這些扇區拼成了一個切開的餅形圖案。
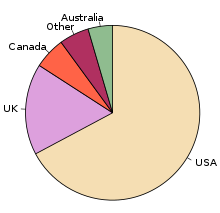

圓形圖在商業領域和大眾媒體中幾乎無處不在,但很少用於科技出版物[1]。這是受到批評最多的圖表之一[2],而很多統計學家建議避免使用這一圖表[3][4]。它們指出,在圓形圖中很難對不同的扇區大小進行比較,或對不同圓形圖之間數據進行比較。在一些特定情況下,圓形圖可以很有效地對資訊進行展示。特別是在想要表示某個大扇區在整體中所佔比例,而不是對不同扇區進行比較時,這一方法十分有效[5]。圓形圖在扇區所佔比例達到總體的25%或50%時,可以很好地達到展示的目的[6]。但通常,可能更多情況會採用其它圖表如條形圖或圓點圖,或非圖表的方法如表格來表達資訊。
通常認為,已知最早的圓形圖是威廉·普萊菲於1801年在他的《統計學摘要》Statistical Breviary中所作[7][5]。
示例
編輯以下數據基於2004年歐洲議會選舉的初步結果。以下表格中列出了分配給各個黨派的席位數量,並計算出了他們各自所佔的百分比。最後一列的數值為每個扇區的圓心角,由360°乘以百分比得到。
| 團體 | 席位 | 百分比 (%) | 圓心角 (°) |
|---|---|---|---|
| EUL | 39 | 5.3 | 19.2 |
| PES | 200 | 27.3 | 98.4 |
| EFA | 42 | 5.7 | 20.7 |
| EDD | 15 | 2.0 | 7.4 |
| ELDR | 67 | 9.2 | 33.0 |
| EPP | 276 | 37.7 | 135.7 |
| UEN | 27 | 3.7 | 13.3 |
| 其它 | 66 | 9.0 | 32.5 |
| 合計 | 732 | 99.9* | 360.2* |
*由於進行取整,合計沒有達到100和360。
每個圓心角的大小都與其所對應的數量成一定比例,在這個例子裏就是席位。由於圓心角的合計需要等於360°,所以一個數量的圓心角就是其在360度中所佔的大小。舉個例子,最大團體(EPP)的圓心角為135.7°。因為360乘以0.377並保留一位小數,等於135.7。
用法討論
編輯統計學家認為將圓形圖用於表達資訊的效果很差。雖然圓形圖在商業領域和雜誌中的使用很廣泛,科學文獻中卻很少用到圓形圖。原因就是圓形圖用面積取代了長度,這樣就加大了對各個數據進行比較的難度。根據史蒂文斯冪函數定律,面積只能提供0.7的感知力,而長度的感知力有1.0。由於感知力的差異與實際差異呈線性相關,長度更適宜用於量度。
根據AT&T貝爾實驗室的研究,使用角度來進行比較沒有使用長度精確。右圖給出了相同數據繪製的三個圓形圖,而下文則是對應的條形圖。在圓形圖中很難根據大小對比較物件進行排序,但條形圖卻很容易做到這一點[8]。同樣,用條形圖更容易進行數據集之間的比較。但是,如果目的是在單一圖表中對一個物件(圓形圖中的扇區)和整體(整個圓形圖)之間的關係進行比較,且比例接近25%的倍數(如25%或50%),圓形圖效果比條形圖好。
變體和類似圖表
編輯分裂式圓形圖
編輯圓形圖中的一個或幾個扇區從圖表中分離開來的形式。這種圖表用於強調某個扇區,或強調圖表中其它占更小比例的扇區。
透視(三維)圓形圖
編輯這種圓形圖樣式用於表現一種三維外觀的圖表。使用這種圖表通常是出於美觀的目的,使用三維外觀並不能改善圖表中數據的讀取。相反,由於使用了三維透視的扭曲效果,這種圖表更難對數據進行分析。通常並不鼓勵使用多餘的維數來美化圖表,這個規律並不只對圓形圖有效。[9]
極區圖
編輯弗羅倫斯·南丁格爾於1858年首次使用了一種現在稱為極區圖的圖表類型,有時也稱為南丁格爾玫瑰圖。這種圖表有時會被錯誤地稱為「雞冠花」("coxcomb"),但這個名稱是南丁格爾用於稱呼使用這一圖表的書,而不是圖表本身[10]。
極區圖和通常使用的圓形圖很類似,扇區的角度和圓形圖一樣但扇區離圓心的距離並不相同。據說南丁格爾早期大部分聲望都來自其對數據清楚且準確的表達。
雖然通常認為南丁格爾發明了這一圖表,但更早之前也有人使用。利昂·拉蘭內於1843年使用極區圖來表示羅經點附近風向的頻率。而André-Michel Guerry是更早的"玫瑰圖"形式發明者,他於1829年的論文就採用它來表示循環現象發生的頻率。
歷史
編輯通常認為,已知最早的圓形圖是威廉·普萊菲於1801年在他的《統計學摘要》Statistical Breviary中所作。書中一共列了兩張這種圖表[7][5]。這一發明最初並沒有得到廣泛應用[5]。查爾斯·約瑟夫·米納爾德於1858年成為第一個使用這一圖表的人,特別是在地圖中增加了相關的三維資訊[11]。
備註
編輯- ^ Cleveland, p. 262
- ^ Wilkinson, p. 23.
- ^ Tufte, p. 178.
- ^ van Belle, p. 160–162.
- ^ 5.0 5.1 5.2 5.3 Spence (2005)
- ^ Good and Hardin, p. 117–118.
- ^ 7.0 7.1 Tufte, p. 44
- ^ Cleveland, p. 86–87
- ^ Good and Hardin, chapter 8.
- ^ Florence Nightingale's Statistical Diagrams. Florence Nightingale Museum. [2006-11-21]. (原始內容存檔於2006-12-07). (頁面存檔備份,存於互聯網檔案館)
- ^ Palsky, p. 144–145
參考文獻
編輯- Cleveland, William S. The Elements of Graphing Data. Pacific Grove, CA: Wadsworth & Advanced Book Program. 1985. ISBN 0-534-03730-5.
- Good, Phillip I. and Hardin, James W. Common Errors in Statistics (and How to Avoid Them). Wiley. 2003. ISBN 0-471-46068-0.
- Guerry, A.-M. (1829). Tableau des variations météorologique comparées aux phénomènes physiologiques, d'aprés les observations faites à l'obervatoire royal, et les recherches statistique les plus récentes. Annales d'Hygiène Publique et de Médecine Légale , 1 :228-.
- Palsky Gilles. Des chiffres et des cartes: la cartographie quantitative au XIXè siècle. Paris: Comité des travaux historiques et scientifiques, 1996. ISBN 2-7355-0336-4.
- Playfair, William, Commercial and Political Atlas and Statistical Breviary, Cambridge University Press (2005) ISBN 0-521-85554-3.
- Spence, Ian. No Humble Pie: The Origins and Usage of a statistical Chart. Journal of Educational and Behavioral Statistics. Winter 2005, 30 (4), 353–368.
- Tufte, Edward. The Visual Display of Quantitative Information. Graphics Press, 2001. ISBN 0-9613921-4-2.
- van Belle, Gerald. Statistical Rules of Thumb. Wiley, 2002. ISBN 0-471-40227-3.
- Wilkinson, Leland. The Grammar of Graphics, 2nd edition. Springer, 2005. ISBN 0-387-24544-8.
參見
編輯外部連結
編輯- (英文)創建你自己的圓形圖 (頁面存檔備份,存於互聯網檔案館)
- (英文)繪製任意的圓形圖 (頁面存檔備份,存於互聯網檔案館)
- (英文)對圓形圖使用的警告 (頁面存檔備份,存於互聯網檔案館)
- (英文)圓形圖 (頁面存檔備份,存於互聯網檔案館) - Edward Tufte的"Ask E.T."論壇
- (英文)極區圖 (頁面存檔備份,存於互聯網檔案館) - Edward Tufte的"Ask E.T."論壇
- (英文)圓形圖工具 (頁面存檔備份,存於互聯網檔案館) - 免費的在線圓形圖生成器,這一工具基於免費軟件JFreeChart。