沃爾什矩陣(英語:Walsh matrix)是一個維度為 的方陣,其中n為自然數。該矩陣由-1和1組成,其所有的行與列都兩兩正交,即點積為0。這一概念由美國數學家約瑟夫·L·沃爾什於1923年提出,故而得名。[1]在沃爾什矩陣中,每一行都和一個沃爾什函數相對應。
的方陣,其中n為自然數。該矩陣由-1和1組成,其所有的行與列都兩兩正交,即點積為0。這一概念由美國數學家約瑟夫·L·沃爾什於1923年提出,故而得名。[1]在沃爾什矩陣中,每一行都和一個沃爾什函數相對應。
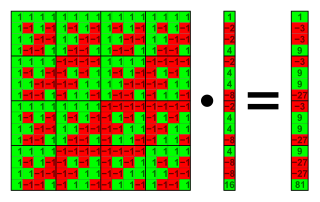 16階的沃爾什矩陣與一個向量相乘
16階的沃爾什矩陣與一個向量相乘
 自然序的阿達瑪矩陣排列成單調變化的阿達瑪矩陣。自然序矩陣中每行符號變化的次數為(0、15、7、8、3、12、4、11、1、14、6、9、2、13、5、10),但是在單調順序矩陣中,符號變化的次數是單調的
自然序的阿達瑪矩陣排列成單調變化的阿達瑪矩陣。自然序矩陣中每行符號變化的次數為(0、15、7、8、3、12、4、11、1、14、6、9、2、13、5、10),但是在單調順序矩陣中,符號變化的次數是單調的
 沃爾什矩陣出現在損壞的TIFF圖像中
沃爾什矩陣出現在損壞的TIFF圖像中
沃爾什矩陣可視為阿達馬矩陣的一個特例,自然有序的阿達馬矩陣是由遞歸公式定義的,序列有序的阿達馬矩陣是通過重新排列行來形成的,這樣一行中的符號變化數就是遞增的。[1]
沃爾什矩陣用於計算沃爾什變換,在信號處理操作中的有實際應用。
維度為 (其中 )的阿達馬矩陣可由遞推的方式進行定義:
-
一般而言
-
其中 且 ,⊗代表克羅內克積。
根據符號變化的次數對所有的行進行重新排列。例如:
-
每行分別有0、3、1、2次符號變化,因此,我們對這些行進行重排:
-
這樣,每行都有0、1、2、3次符號變化。
沃爾什矩陣的行順序可以通過阿達馬矩陣首先經過位序顛倒排列,然後經過格雷碼排列得到:[2]
-
其中每行分別有0、1、2、3、4、5、6、7次符號改變。



