牛奶凍曲線
此條目需要精通或熟悉相關主題的編者參與及協助編輯。 (2019年7月20日) |
此條目沒有列出任何參考或來源。 (2019年7月20日) |
牛奶凍曲線(blancmange curve)又稱為高木曲線,因為在1901年由高木貞治所研究。另外也稱為 Takagi-Landsberg 曲線,一種更一般化的曲線,以高木貞治和 Georg Landsberg 的名字命名。 牛奶凍曲線也是 de Rham 曲線的特例。
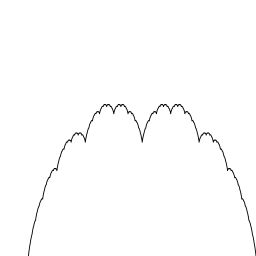
定義
編輯定義域為單位區間的牛奶凍函數定義為
其中 是三角波函數,定義為 。
而 Takagi–Landsberg 曲線的定義是更一般化的:
其中 是一個變數使 。
-
parameter w=2/3
-
parameter w=1/2
-
parameter w=1/3
-
parameter w=1/4
-
parameter w=1/8
性質
編輯收斂與連續性
編輯以 ( )為參數無限和 對所有 絕對收斂:因為對所有 有 ,從而
- 。
- 對所有 。
其值在 夠大時可以任意的小。再根據均勻極限定理, 連續。
次可加性
編輯具有次可加性。
拋物線
編輯當 , 的圖形是拋物線,且用中點細分的構造方法曾被阿基米德描述。
可微性
編輯對所有 , 在任意不是二進分數的 是可微的,且其結果是
其中 是 的二進位表達式的序列,也就是滿足 的序列。