薄膜生长模式
薄膜生长模式(Modes of thin-film growth)指的是薄膜在材料表面的外延成长中不同的生长机制,由恩斯特·鲍尔于1958年系统化地归纳为三大类型[1]:岛状生长模式(即Volmer-Weber模式)、层状生长模式(即Frank–van der Merwe模式)和岛状/层状生长模式(即斯特兰斯基-克拉斯坦诺夫模式)[注 1]。
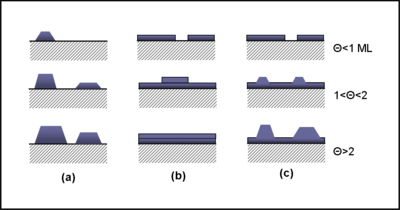



基本生长模式
编辑岛状生长模式
编辑岛状生长模式又称Volmer-Weber模式、VM模式,得名于马克斯·福尔默和A. 韦伯[4]。在岛状生长中,薄膜原子相互之间的束缚力强于衬底对薄膜原子的束缚力,导致薄膜原子在衬底表面直接成核生长出三维的原子岛[5]。大部分薄膜都是呈岛状生长的[6]。
层状生长模式
编辑层状生长模式又称Frank–van der Merwe模式、FM模式,得名于弗雷德里克·查尔斯·弗兰克和Jan H van der Merwe[7][8][9]。在层状生长中,衬底对薄膜原子的束缚力强于薄膜原子之间的作用力,导致薄膜遵循严格的二维生长——即直到完全生长完一层,下一层才开始生长[5]。层状生长模式在PbSe/PbS、Au/Pd、Fe/Cu等系统中有出现[6]。
岛状/层状生长模式
编辑岛状/层状生长模式又称斯特兰斯基-克拉斯坦诺夫模式、SK模式,得名于伊万·斯特兰斯基和 Lyubomir Krastanov[10]。岛状/层状生长模式介于岛状生长模式与层状生长模式之间:在衬底上以二维方式生长一定厚度的薄膜之后,会开始以三维形式生长原子岛。[5]岛状/层状生长模式在Cd/W、Cd/Ge等系统中出现[6]。
理论解释
编辑不同的薄膜生长模式取决于薄膜和衬底材料表面的化学与物理性质,例如表面张力和晶格系数[11][12][5],可通过考虑距离表面最近的几层原子的化学势来确定生长机制[12][13]。1995年,伊万·马尔可夫提出原子层内单原子的化学势模型[13]:
其中 表示吸附材料的体化学势(bulk chemical potential), 表示浸润层吸附原子的脱附能(desorption energy), 表示衬底吸附原子的脱附能, 表示每个原子的位错错配能(misfit dislocation energy), 表示每个原子的同质应变能(homogeneous strain energy)。在一般情况下, 、 、 和 的值与薄膜的厚度,以及衬底和薄膜之间的位错有着极为复杂的关系。在应变很小的情况下(即 ),薄膜的生长模式取决于 的值:
实验测量
编辑在实际的科学实验中,可以运用多种手段判断薄膜生长的模式,包括透射电子显微镜或扫描隧道显微镜(直接测量表面形貌),低能电子衍射或反射式高能电子衍射(通过测量衍射强度的振荡),以及俄歇电子能谱[5]。
注释
编辑参考文献
编辑- ^ Bauer, Ernst. Phänomenologische Theorie der Kristallabscheidung an Oberflächen. I. Zeitschrift für Kristallographie. 1958, 110: 372–394. Bibcode:1958ZK....110..372B. doi:10.1524/zkri.1958.110.1-6.372.
- ^ 江绍基. 薄膜生长与制备技术 (PDF). 中山大学. [2017-10-13]. (原始内容存档 (PDF)于2017-10-14).
- ^ 林 智広. 金属薄膜標準物質の現状,ニーズ,技術背景に関する報告 (PDF). 産総研計量標準報告. 2007-03, 6 (1): 64.
- ^ Volmer, M.; Weber, A. Keimbildung in übersättigten Gebilden. Z. Phys. Chem. 1926, 119: 277–301.
- ^ 5.0 5.1 5.2 5.3 5.4 Oura, K.; V.G. Lifshits; A.A. Saranin; A.V. Zotov; M. Katayama. Surface Science: An Introduction. Berlin: Springer. 2003. ISBN 3-540-00545-5.
- ^ 6.0 6.1 6.2 8.关于薄膜制造上的重点. SHINCRON Co.,Ltd. [2017-10-13]. (原始内容存档于2016-09-13).
- ^ Frank, F. C.; van der Merwe, J. H. One-Dimensional Dislocations. I. Static Theory. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 1949, 198 (1053): 205–216. Bibcode:1949RSPSA.198..205F. JSTOR 98165. doi:10.1098/rspa.1949.0095.
- ^ Frank, F. C.; van der Merwe, J. H. One-Dimensional Dislocations. II. Misfitting Monolayers and Oriented Overgrowth. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 1949, 198 (1053): 216–225. Bibcode:1949RSPSA.198..216F. JSTOR 98166. doi:10.1098/rspa.1949.0096.
- ^ Frank, F. C.; van der Merwe, J. H. One-Dimensional Dislocations. III. Influence of the Second Harmonic Term in the Potential Representation, on the Properties of the Model. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 1949, 200 (1060): 125–134. Bibcode:1949RSPSA.200..125F. JSTOR 98394. doi:10.1098/rspa.1949.0163.
- ^ Stranski, I. N.; Krastanov, L. Zur Theorie der orientierten Ausscheidung von Ionenkristallen aufeinander. Sitzungsber. Akad. Wiss. Wien. Math.-Naturwiss. 1938, 146: 797–810.
- ^ Venables, John. Introduction to Surface and Thin Film Processes. Cambridge: Cambridge University Press. 2000. ISBN 0-521-62460-6.
- ^ 12.0 12.1 Pimpinelli, Alberto; Jacques Villain. Physics of Crystal Growth. Cambridge: Cambridge University Press. 1998. ISBN 0-521-55198-6.
- ^ 13.0 13.1 13.2 Markov, Ivan V. Crystal Growth for Beginners: Fundamentals of Nucleation, Crystal Growth, and Epitaxy. Singapore: World Scientific. 1995. ISBN 981-02-1531-2.