凱利公式
凱利公式、凱利方程式、凱利判據、凱利策略(英語:Kelly criterion、Kelly strategy、Kelly bet),是一種根據賭博贏或輸的機率,計算出每次下注的資金占所有賭本的最佳比例的公式[1],由約翰·拉里·凱利於1956年在《貝爾系統技術期刊》中發表,可用以計算出每次遊戲中應投注的資金比例。除可將長期增長率最大化外,此方程式不允許在任何賭局中,有失去全部現有資金的可能,因此有不存在破產疑慮的優點。方程式假設貨幣與賭局可無窮分割,而只要資金足夠多,在實際應用上不成問題。
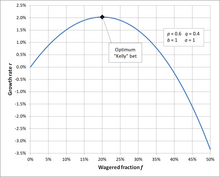


陳述
編輯凱利公式的最一般性陳述為,藉由尋找能最大化結果對數期望值的資本比例f*,即可獲得長期增長率的最大化。對於只有兩種結果的簡單賭局:要麼輸掉所有注金,要麼贏得注金乘以特定賠率,公式的一般性陳述為:
其中
- f*為現有資金應進行下次投注的比例;
- b為投注可得的賠率(不含本金);
- p為獲勝率;
- q為落敗率,即1 - p;
舉例而言,若一賭博有60%的獲勝率(p = 0.6,q = 0.4),而且賭客在贏得賭局時,可獲得一賠一的賠率(b = 1),則賭客應在每次機會中下注現有資金的20%(f* = 0.2),以最大化資金的長期增長率。 如果賠率沒有優勢,即 b < q / p,公式的結果是負的,那麼公式建議不下注。 如果賠率是負的,即b < 0,也就是暗示應該下注到另外一邊。
凱利公式最初為AT&T貝爾實驗室物理學家約翰·拉里·凱利根據同僚克勞德·艾爾伍德·夏農於長途電話線雜訊上的研究所建立。凱利說明夏農的資訊理論要如何應用於一名擁有內線消息的賭徒在賭馬時的問題。賭徒希望決定最佳的賭金額,而他的內線消息不需完美(無雜訊),即可讓他擁有有用的優勢。凱利的公式隨後被夏農的另一名同僚愛德華·索普應用於二十一點和股票市場中。[2]
證明
編輯凱利公式的目標是最大化資產的增長率,也即最大化對數資產的期望值。不失一般性,設開始時的資產是1,每次下注的比例為 ,有 的機率會以 的賠率贏錢,這時資產變為 。如果輸了,資產就是 。因此資產的對數的期望值為
要找到最大化這個期望值的 ,只需令 對 的導數值為零:
求解上述方程式即得凱利公式
在凱利最初發表的論文中有著更一般而更嚴謹的證明[3]。
劣勢
編輯凱利公式原本是為了協助規劃電子比特流量設計,後來被引用於賭二十一點上去,麻煩就出在一個簡單的事實,二十一點並非商品或交易。賭二十一點時,可能會輸的賭本只限於所放進去的籌碼,而可能會贏的利潤,也只限於賭注籌碼的範圍。但商品交易輸贏程度是沒得準的,會造成資產或輸贏有很大的震幅。
較早的發現
編輯1738年丹尼爾·伯努利曾提出等價的觀點,可是伯努利的文章直到1954年才首次譯成英語。不過對於只投資一次的人來說,應選擇算術平均最高的投資組合。[4]
參考
編輯- ^ 書名: 《證券投資理論精要》 作者: 周朝鴻 當前第:182頁
- ^ American Scientist online: Bettor Math, article and book review by Elwyn Berlekamp. [2006-08-21]. (原始內容存檔於2006-07-11).
- ^ Kelly, J. L. A New Interpretation of Information Rate (PDF). Bell System Technical Journal. 1956, 35 (4): 917–926 [2019-04-20]. doi:10.1002/j.1538-7305.1956.tb03809.x. (原始內容存檔 (PDF)於2019-04-27).
- ^ William Poundstone, Fortune's Formula: The Untold Story of the Scientific Betting System That Beat the Casinos and Wall Street, Hill and Wang, New York, 2005