動態光散射
動態光散射,也稱作光子相關光譜或准彈性光散射,是一種物理表徵手段,用來測量溶液或懸浮液中的粒徑分布,[1]也可以用來測如量高分子濃溶液等的複雜流體的行為。
原理
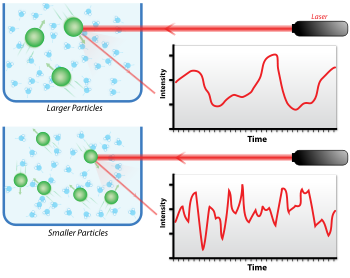
編輯當光射到遠小於其波長的小顆粒上時,光會向各方向散射(瑞利散射)。如果光源是雷射,在某一方向上,我們可以觀察到散射光的強度隨時間而波動,這是因為溶液中的微小顆粒在做布朗運動,且每個發生散射的顆粒之間的距離一直隨時間變化。來自不同顆粒的散射光因相位不同產生建設性或破壞性干涉。所得到的強度隨時間波動的曲線帶有引起散射的顆粒隨時間移動的資訊。動態光散射實驗易受灰塵或雜質影響,故樣品的過濾和離心十分重要。
顆粒的運動資訊可通過實驗中記錄到的散射光強度的自相關函數導出,二階自相關曲函數的推導如下:
此處的 是選定的波向量 的自相關函數, 是延遲時間, 是散射光的強度。當延遲時間較短時,相關性較高,因為顆粒的移動距離短。故相差很短時間的兩個訊號沒有顯著差別。當延遲時間較長時,相關性呈指數衰減趨勢,意味著經歷較長時間後,兩組訊號的散射光強度沒有相關性。這一指數衰減的快慢和顆粒的運動特性關係密切,特別取決於擴散係數。基於假設分布的數學方法被用於與相關性相擬合。如果樣品是單分散的,衰減是簡單的指數關係。Siegert公式將二階自我相關函數和一階自我相關函數 聯繫起來:
此處的參數β是取決於顆粒的集合形狀的校正係數。它約等於speckles數目的反比。當雷射束聚焦在較小的區域上時,會導致較粗糙的speckle pattern,探測器收集到較少的speckle,形成較大的二階自相關函數。
多分散指數(Polydiseperse Index,PDI),即相對偏差(Relative variance),是指示分散度的重要指標,PDI = sigma2/ZD2,其中sigma是標準偏差,Z是Z平均尺寸。分散度(Polydispersity,Pd),是標準偏差(Standard deviation)、寬度(width)、絕對分散試(absolute polydispersity),或百分分散度(Polydispersity,%Pd)也就是偏差因子(Coefficient of variation)。其中%Pd = (PdI)1/2 × 100,也稱作相對分散度。[2]
應用
編輯動態光散射用於表徵蛋白質、高分子、膠束、糖和納米顆粒的尺寸。如果系統是單分散的,顆粒的平均有效直徑可以求出來,這一測量取決於顆粒的心,表面結構,顆粒的濃度和介質中的離子種類。DLS也可以用於穩定性研究,通過測量不同時間的粒徑分布,可以展現顆粒隨時間聚沉的趨勢。隨著微粒的聚沉,具有較大粒徑的顆粒變多。同樣,DLS也可以用來分析溫度對穩定性的影響。
推薦書籍
編輯《雷射光散射譜學》張明生著 科學出版社, 2008.5 《Laser light scattering》Chu, Benjamin著.New York, Academic Press, 1974.
參考資料
編輯- ^ Berne, B.J.; Pecora, R. Dynamic Light Scattering; Wiley: New York, 1976
- ^ "Dynamic light scattering and application to proteins in solutions"http://mafija.fmf.uni-lj.si/seminar/files/2009_2010/Dynamic_light_scattering_and_application_to_proteins_in_solutions.pdf (頁面存檔備份,存於網際網路檔案館)