-
-
-
-
| Tanc abs complex 3D
|
Tanc Im complex 3D plot
|
Tanc Re complex 3D plot
|
| Tanc'(z) Im complex 3D plot
|
Tanc'(z) Re complex 3D plot
|
Tanc'(z) abs complex 3D plot
|
|
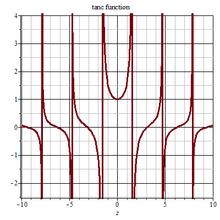
| Tanc abs plot
|
Tanc Im plot
|
Tanc Re plot
|
| Tanc'(z) Im plot
|
Tanc'(z) abs plot
|
Tanc'(z) Re plot
|
| Tanc integral abs plot
|
Tanc integral Im plot
|
Tanc integral Re plot
|
| Tanc abs complex 3D plot
|
Tanc Im complex 3D plot
|
Tanc Re complex 3D plot
|