二元搜尋樹
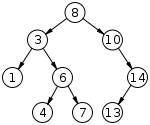
二叉查找树(英語:Binary Search Tree),也称为二叉搜索树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
| Binary search tree | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 类型 | 樹 | ||||||||||||||||||||
| 发明时间 | 1960年 | ||||||||||||||||||||
| 发明者 | P·F·溫德利、安德鲁·唐纳德·布思、安德鲁·科林、托馬斯·N·希巴德 | ||||||||||||||||||||
| 用大O符号表示的时间复杂度 | |||||||||||||||||||||
| |||||||||||||||||||||
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为。二叉查找树是基础性数据结构,用于构建更为抽象的数据结构,如集合、多重集、关联数组等。
二叉查找树的查找过程和次优二叉树类似,通常采取二叉链表作为二叉查找树的存储结构。中序遍历二叉查找树可得到一个关键字的有序序列,一个无序序列可以透過建構一棵二叉查找树变成一个有序序列,建構树的过程即为对无序序列进行查找的过程。每次插入的新的结点都是二叉查找树上新的叶子结点,在进行插入操作时,不必移动其它结点,只需改动某个结点的指针,由空变为非空即可。搜索、插入、删除的复杂度等于树高,期望,最坏退化為偏斜二元樹。對於可能形成偏斜二元樹的問題可以經由樹高改良後的平衡樹將搜尋、插入、刪除的時間複雜度都維持在,如AVL树、红黑树等。
二叉查找树的查找算法
编辑在二叉查找树b中查找x的過程為:
- 若b是空樹,則搜索失敗,否則:
- 若x等於b的根節點的數據域之值,則查找成功;否則:
- 若x小於b的根節點的數據域之值,則搜索左子樹;否則:
- 查找右子树。
在二叉搜索树的可视化页面可以看到查找节点的动画过程。其中实现代码如下:
Status SearchBST(BiTree T, KeyType key, BiTree f, BiTree &p) {
// 在根指针T所指二叉查找树中递归地查找其關键字等於key的數據元素,若查找成功,
// 則指针p指向該數據元素節點,并返回TRUE,否則指针指向查找路徑上訪問的最後
// 一個節點并返回FALSE,指针f指向T的雙親,其初始调用值為NULL
if (!T) { // 查找不成功
p = f;
return false;
} else if (key == T->data.key) { // 查找成功
p = T;
return true;
} else if (key < T->data.key) // 在左子樹中繼續查找
return SearchBST(T->lchild, key, T, p);
else // 在右子樹中繼續查找
return SearchBST(T->rchild, key, T, p);
}
在二叉查找树插入節点的算法
编辑向一个二元搜尋樹b中插入一个節点s的算法,过程为:
- 若b是空树,则将s所指節点作为根節点插入,否则:
- 若s->data等于b的根節点的数据域之值,则返回,否则:
- 若s->data小于b的根節点的数据域之值,则把s所指節点插入到左子树中,否则:
- 把s所指節点插入到右子树中。(新插入節點總是葉子節點)
/* 当二元搜尋樹T中不存在关键字等于e.key的数据元素时,插入e并返回TRUE,否则返回 FALSE */
Status InsertBST(BiTree *&T, ElemType e) {
if (!T) {
s = new BiTNode;
s->data = e;
s->lchild = s->rchild = NULL;
T = s; // 被插節点*s为新的根结点
} else if (e.key == T->data.key)
return false;// 关键字等于e.key的数据元素,返回錯誤
if (e.key < T->data.key)
InsertBST(T->lchild, e); // 將 e 插入左子樹
else if (e.key > T->data.key)
InsertBST(T->rchild, e); // 將 e 插入右子樹
return true;
}
在二叉查找树删除结点的算法
编辑在二叉查找树删去一个结点,分三种情况讨论:
- 若*p结点为叶子结点,即PL(左子树)和PR(右子树)均为空树。由于删去叶子结点不破坏整棵树的结构,则只需修改其双亲结点的指针即可。
- 若*p结点只有左子树PL或右子树PR,此时只要令PL或PR直接成为其双亲结点*f的左子树(当*p是左子树)或右子树(当*p是右子树)即可,作此修改也不破坏二叉查找树的特性。
- 若*p结点的左子树和右子树均不空。在删去*p之后,为保持其它元素之间的相对位置不变,可按中序遍历保持有序进行调整,可以有两种做法:其一是令*p的左子树为*f的左/右(依*p是*f的左子树还是右子树而定)子树,*s为*p左子树的最右下的结点,而*p的右子树为*s的右子树;其二是令*p的直接前驱(in-order predecessor)或直接后继(in-order successor)替代*p,然后再从二叉查找树中删去它的直接前驱(或直接后继)。
在二叉查找树上删除一个结点的算法如下:
Status DeleteBST(BiTree *T, KeyType key) {
// 若二叉查找树T中存在关键字等于key的数据元素时,则删除该数据元素,并返回
// TRUE;否则返回FALSE
if (!T)
return false; //不存在关键字等于key的数据元素
else {
if (key == T->data.key) // 找到关键字等于key的数据元素
return Delete(T);
else if (key < T->data.key)
return DeleteBST(T->lchild, key);
else
return DeleteBST(T->rchild, key);
}
}
Status Delete(BiTree *&p) {
// 该节点为叶子节点,直接删除
BiTree *q, *s;
if (!p->rchild && !p->lchild) {
delete p;
p = NULL; // Status Delete(BiTree *&p) 要加&才能使P指向NULL
} else if (!p->rchild) { // 右子树空则只需重接它的左子树
q = p->lchild;
/*
p->data = p->lchild->data;
p->lchild=p->lchild->lchild;
p->rchild=p->lchild->rchild;
*/
p->data = q->data;
p->lchild = q->lchild;
p->rchild = q->rchild;
delete q;
} else if (!p->lchild) { // 左子树空只需重接它的右子树
q = p->rchild;
/*
p->data = p->rchild->data;
p->lchild=p->rchild->lchild;
p->rchild=p->rchild->rchild;
*/
p->data = q->data;
p->lchild = q->lchild;
p->rchild = q->rchild;
delete q;
} else { // 左右子树均不空
q = p;
s = p->lchild;
while (s->rchild) {
q = s;
s = s->rchild;
} // 转左,然后向右到尽头
p->data = s->data; // s指向被删结点的“前驱”
if (q != p)
q->rchild = s->lchild; // 重接*q的右子树
else
q->lchild = s->lchild; // 重接*q的左子树
delete s;
}
return true;
}
在C语言中有些编译器不支持为struct Node 节点分配空间,声称这是一个不完全的结构,可使用一个指向该Node的指针为之分配空间。
- 如:
sizeof( Probe ),Probe作为二叉树节点在typedef中定义的指针。
Python实现:
def find_min(self): # Gets minimum node (leftmost leaf) in a subtree
current_node = self
while current_node.left_child:
current_node = current_node.left_child
return current_node
def replace_node_in_parent(self, new_value=None):
if self.parent:
if self == self.parent.left_child:
self.parent.left_child = new_value
else:
self.parent.right_child = new_value
if new_value:
new_value.parent = self.parent
def binary_tree_delete(self, key):
if key < self.key:
self.left_child.binary_tree_delete(key)
elif key > self.key:
self.right_child.binary_tree_delete(key)
else: # delete the key here
if self.left_child and self.right_child: # if both children are present
successor = self.right_child.find_min()
self.key = successor.key
successor.binary_tree_delete(successor.key)
elif self.left_child: # if the node has only a *left* child
self.replace_node_in_parent(self.left_child)
elif self.right_child: # if the node has only a *right* child
self.replace_node_in_parent(self.right_child)
else: # this node has no children
self.replace_node_in_parent(None)
二叉查找树的遍历
编辑中序遍历(in-order traversal)二叉查找树的Python代码:
def traverse_binary_tree(node, callback):
if node is None:
return
traverse_binary_tree(node.leftChild, callback)
callback(node.value)
traverse_binary_tree(node.rightChild, callback)
排序(或称构造)一棵二叉查找树
编辑用一组数值建造一棵二叉查找树的同时,也把这组数值进行了排序。其最差时间复杂度为 。例如,若该组数值已经是有序的(从小到大),则建造出来的二叉查找树的所有节点,都没有左子树。自平衡二叉查找树可以克服上述缺点,其时间复杂度为O(nlog n)。一方面,树排序的问题使得CPU Cache性能较差,特别是当节点是动态内存分配时。而堆排序的CPU Cache性能较好。另一方面,树排序是最优的增量排序(incremental sorting)算法,保持一个数值序列的有序性。
def build_binary_tree(values):
tree = None
for v in values:
tree = binary_tree_insert(tree, v)
return tree
def get_inorder_traversal(root):
'''
Returns a list containing all the values in the tree, starting at *root*.
Traverses the tree in-order(leftChild, root, rightChild).
'''
result = []
traverse_binary_tree(root, lambda element: result.append(element))
return result
二叉查找树性能分析
编辑每个结点的 为该结点的层次数。最坏情况下,当先后插入的关键字有序时,构成的二叉查找树蜕变为单支树,树的深度为 ,其平均查找长度为 (和顺序查找相同),最好的情况是二叉查找树的形态和折半查找的判定树相同,其平均查找长度和 成正比( )。
二叉查找树的优化
编辑一般的二叉查找树的查询复杂度取决于目标结点到树根的距离(即深度),因此当结点的深度普遍较大时,查询的均摊复杂度会上升。为了实现更高效的查询,产生了平衡树。在这里,平衡指所有叶子的深度趋于平衡,更广义的是指在树上所有可能查找的均摊复杂度偏低。
参见
编辑外部链接
编辑- 二叉搜索树的可视化页面 支持动画显示二叉搜索树的插入,查找和删除操作。
- Literate implementations of binary search trees in various languages(页面存档备份,存于互联网档案馆) on LiteratePrograms
- Binary Tree Visualizer(页面存档备份,存于互联网档案馆) (JavaScript animation of various BT-based data structures)
- Kovac, Kubo. Binary Search Trees. Korešponden?ný seminár z programovania. [2018-04-29]. (原始内容 (Java applet)存档于2018-04-30). (页面存档备份,存于互联网档案馆)
- Madru, Justin. Binary Search Tree. JDServer. 18 August 2009 [2018-04-29]. (原始内容存档于2010-03-28). (页面存档备份,存于互联网档案馆) C++ implementation.
- Binary Search Tree Example in Python(页面存档备份,存于互联网档案馆)
- References to Pointers (C++). 微软开发者网络. 微软. 2005 [2018-04-29]. (原始内容存档于2017-03-29). (页面存档备份,存于互联网档案馆) Gives an example binary tree implementation.

