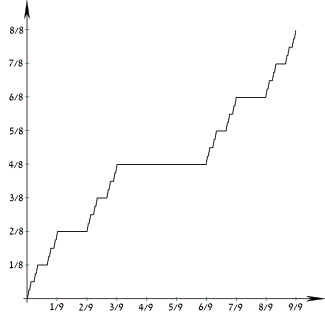
康托尔分布的基础是康托集 ，本身是多个可数无限集的交:
C
0
=
[
0
,
1
]
C
1
=
[
0
,
1
/
3
]
∪
[
2
/
3
,
1
]
C
2
=
[
0
,
1
/
9
]
∪
[
2
/
9
,
1
/
3
]
∪
[
2
/
3
,
7
/
9
]
∪
[
8
/
9
,
1
]
C
3
=
[
0
,
1
/
27
]
∪
[
2
/
27
,
1
/
9
]
∪
[
2
/
9
,
7
/
27
]
∪
[
8
/
27
,
1
/
3
]
∪
[
2
/
3
,
19
/
27
]
∪
[
20
/
27
,
7
/
9
]
∪
[
8
/
9
,
25
/
27
]
∪
[
26
/
27
,
1
]
C
4
=
[
0
,
1
/
81
]
∪
[
2
/
81
,
1
/
27
]
∪
[
2
/
27
,
7
/
81
]
∪
[
8
/
81
,
1
/
9
]
∪
[
2
/
9
,
19
/
81
]
∪
[
20
/
81
,
7
/
27
]
∪
[
8
/
27
,
25
/
81
]
∪
[
26
/
81
,
1
/
3
]
∪
[
2
/
3
,
55
/
81
]
∪
[
56
/
81
,
19
/
27
]
∪
[
20
/
27
,
61
/
81
]
∪
[
62
/
81
,
21
/
27
]
∪
[
8
/
9
,
73
/
81
]
∪
[
74
/
81
,
25
/
27
]
∪
[
26
/
27
,
79
/
81
]
∪
[
80
/
81
,
1
]
C
5
=
⋯
{\displaystyle {\begin{aligned}C_{0}={}&[0,1]\\[8pt]C_{1}={}&[0,1/3]\cup [2/3,1]\\[8pt]C_{2}={}&[0,1/9]\cup [2/9,1/3]\cup [2/3,7/9]\cup [8/9,1]\\[8pt]C_{3}={}&[0,1/27]\cup [2/27,1/9]\cup [2/9,7/27]\cup [8/27,1/3]\cup \\[4pt]{}&[2/3,19/27]\cup [20/27,7/9]\cup [8/9,25/27]\cup [26/27,1]\\[8pt]C_{4}={}&[0,1/81]\cup [2/81,1/27]\cup [2/27,7/81]\cup [8/81,1/9]\cup [2/9,19/81]\cup [20/81,7/27]\cup \\[4pt]&[8/27,25/81]\cup [26/81,1/3]\cup [2/3,55/81]\cup [56/81,19/27]\cup [20/27,61/81]\cup \\[4pt]&[62/81,21/27]\cup [8/9,73/81]\cup [74/81,25/27]\cup [26/27,79/81]\cup [80/81,1]\\[8pt]C_{5}={}&\cdots \end{aligned}}}
康托尔分布对任何 C t t ∈ { 0, 1, 2, 3, ... }) 中 2t -t .
通过对称性很容易看出，具有这样分布的一个随机变量 X，其期望值 E(X ) = 1/2，且所有 X 的奇数阶中心矩都是 0。
方差 var(X ) 可由总方差定律 C 1 ，如果 X ∈ [0,1/3] 则令 Y = 0，如果 X ∈ [的2/3，1]，令 Y = 1。然后有
var
(
X
)
=
E
(
var
(
X
∣
Y
)
)
+
var
(
E
(
X
∣
Y
)
)
=
1
9
var
(
X
)
+
var
{
1
/
6
with probability
1
/
2
5
/
6
with probability
1
/
2
}
=
1
9
var
(
X
)
+
1
9
{\displaystyle {\begin{aligned}\operatorname {var} (X)&=\operatorname {E} (\operatorname {var} (X\mid Y))+\operatorname {var} (\operatorname {E} (X\mid Y))\\&={\frac {1}{9}}\operatorname {var} (X)+\operatorname {var} \left\{{\begin{matrix}1/6&{\mbox{with probability}}\ 1/2\\5/6&{\mbox{with probability}}\ 1/2\end{matrix}}\right\}\\&={\frac {1}{9}}\operatorname {var} (X)+{\frac {1}{9}}\end{aligned}}}
从而我们得到：
var
(
X
)
=
1
8
.
{\displaystyle \operatorname {var} (X)={\frac {1}{8}}.}
任意偶数阶中心矩的封闭表达式可由：先获得偶数项累积量 [1] （页面存档备份 ，存于互联网档案馆 ）
κ
2
n
=
2
2
n
−
1
(
2
2
n
−
1
)
B
2
n
n
(
3
2
n
−
1
)
,
{\displaystyle \kappa _{2n}={\frac {2^{2n-1}(2^{2n}-1)B_{2n}}{n\,(3^{2n}-1)}},\,\!}
其中 B 2n 是 第2n 个 伯努利数 ，然后用该累积量的方程作为矩的表达。
Falconer, K. J. Geometry of Fractal Sets. Cambridge & New York: Cambridge Univ Press. 1985. Hewitt, E.; Stromberg, K. Real and Abstract Analysis . Berlin-Heidelberg-New York: Springer-Verlag. 1965. Hu, Tian-You; Lau, Ka Sing. Fourier Asymptotics of Cantor Type Measures at Infinity. Proc. A.M.S. 130 (9). 2002: 2711–2717. Knill, O. Probability Theory & Stochastic Processes. India: Overseas Press. 2006. Mandelbrot, B. The Fractal Geometry of Nature . San Francisco, CA: WH Freeman & Co. 1982. Mattilla, P. Geometry of Sets in Euclidean Spaces. San Francisco: Cambridge University Press. 1995. Saks, Stanislaw. Theory of the Integral. Warsaw: PAN. 1933. 
![{\displaystyle {\begin{aligned}C_{0}={}&[0,1]\\[8pt]C_{1}={}&[0,1/3]\cup [2/3,1]\\[8pt]C_{2}={}&[0,1/9]\cup [2/9,1/3]\cup [2/3,7/9]\cup [8/9,1]\\[8pt]C_{3}={}&[0,1/27]\cup [2/27,1/9]\cup [2/9,7/27]\cup [8/27,1/3]\cup \\[4pt]{}&[2/3,19/27]\cup [20/27,7/9]\cup [8/9,25/27]\cup [26/27,1]\\[8pt]C_{4}={}&[0,1/81]\cup [2/81,1/27]\cup [2/27,7/81]\cup [8/81,1/9]\cup [2/9,19/81]\cup [20/81,7/27]\cup \\[4pt]&[8/27,25/81]\cup [26/81,1/3]\cup [2/3,55/81]\cup [56/81,19/27]\cup [20/27,61/81]\cup \\[4pt]&[62/81,21/27]\cup [8/9,73/81]\cup [74/81,25/27]\cup [26/27,79/81]\cup [80/81,1]\\[8pt]C_{5}={}&\cdots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/066362d7de9b7a1d0bcf600d1dd5a2fcb9196ae4)
