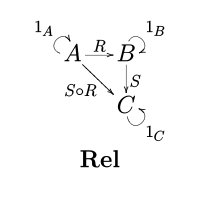
關係範疇
在數學上,關係範疇(記做Rel)指的是以集合為物件、以二元關係為態射的範疇。
在這個範疇中,其態射是與之間的關係,因此
這範疇中兩個關係及的合成由下式給出:
,若且唯若對於一些而言,且[1]
關係範疇又被一些人稱為「集合間對應的範疇」(category of correspondences of sets)。[2]
性質
编辑集合範疇是關係範疇的(寬)子範疇,其中集合範疇的態射 對應至以 定義的關係 。[3][4]
關係範疇中的態射為關係,而其相對應的、從其反範疇映至關係範疇的態射有著反向的箭頭,因此這態射是個逆關係,因此關係範疇包含其反範疇且是個自雙對。[5]
由逆關係作代表所建構的對合為關係範疇提供了一個短劍結構,因此關係範疇是一個短劍範疇。
關係範疇有兩個做為同態函子並映至自己的函子,其中一個是二元關係 ,另一個則是其轉置 ,而這兩個二元關係的兩種合成關係分別為 及 ,其中第一個合成關係 給出了A上的齊次關係;而第二個合成關係 則給出B上的齊次關係。由於這些函子是映至關係範疇自身的同態函子之故,因此這些同態函子是內部同態函子;而由於這些內部同態函子之故,因此關係範疇是個閉範疇,且是個短劍緊緻範疇。
關係範疇可以克萊斯利範疇的形式,由集合範疇得到,在這種狀況下,其有著以對應至冪集的函子為協變函子的單子。
一個第一眼看上去可能令人有點驚訝的事實是,關係範疇當中的乘法是以不相交聯集(而非如集合範疇一般的笛卡爾積)定義的[5]:181,而其餘積亦然。
就其幺半乘積 與內部同態函子 而言,關係範疇是個閉幺半範疇。
關係範疇是Peter J. Freyd與Andre Scedrov在1990年給出的代數結構寓範疇的原型[6],他們自正則範疇與 出發,他們注意到了派生函子 的性質,像例如說這函子保存了合成、逆轉跟相交等運算,而他們之後以這樣的性質建構了寓範疇的公理。
關係作為物件
编辑David Rydeheard與Rod Burstall認為關係範疇有著作為齊次關係物件,一個例子是 是一個集合而 是一個二元關係;而這個範疇的態射是集合間保持關係的函數,在 是第二個關係且 是一個使得 成立的函數,那 是一個態射。[7]
Adamek、Herrlich與Strecker三氏進一步發展了這想法,他們將物件 與 給設成(集合,關係)。[8]
參考資料
编辑- ^ Mac Lane, S. Categories for the Working Mathematician 1st. New York: Springer-Verlag. 1988: 26. ISBN 0-387-90035-7.
- ^ Pareigis, Bodo. Categories and Functors. Pure and Applied Mathematics 39. Academic Press. 1970: 6. ISBN 978-0-12-545150-5.
- ^ Rydeheard與Burstall二氏將此範疇給記做SetRel
- ^ George Bergman (1998), An Invitation to General Algebra and Universal Constructions (页面存档备份,存于互联网档案馆), §7.2 RelSet, Henry Helson Publisher, Berkeley. ISBN 0-9655211-4-1.
- ^ 5.0 5.1 Michael Barr & Charles Wells (1998) Category Theory for Computing Science 互联网档案馆的存檔,存档日期2016-03-04., page 83, from McGill University
- ^ Peter J. Freyd & Andre Scedrov (1990) Categories, Allegories, pages 79, 196, North Holland ISBN 0-444-70368-3
- ^ David Rydeheard & Rod Burstall (1988) Computational Category Theory, page 41, Prentice-Hall ISBN 978-0131627369
- ^ Juri Adamek, Horst Herrlich, and George E. Strecker (2004) [1990] Abstract and Concrete Categories (页面存档备份,存于互联网档案馆), section 3.3, example 2(d) page 22, from Research group KatMAT (页面存档备份,存于互联网档案馆) at University of Bremen
- Francis Borceux. Handbook of Categorical Algebra: Volume 2, Categories and Structures. Cambridge University Press. 1994: 115 [2022-07-14]. ISBN 978-0-521-44179-7. (原始内容存档于2022-07-14).