大十二面二十面六十面体
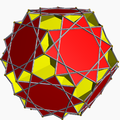
在几何学中,大十二面二十面六十面体(Great dodecicosacron)是一种星形多面体,由60个全等且互相相交的领结形面组成,是均匀多面体——大十二面二十面体的对偶多面体[1]。
 | ||
| 类别 | 均匀多面体对偶 星形多面体 | |
|---|---|---|
| 对偶多面体 | 大十二面二十面体 | |
| 识别 | ||
| 名称 | 大十二面二十面六十面体 | |
| 参考索引 | DU63 | |
| 性质 | ||
| 面 | 60 | |
| 边 | 120 | |
| 顶点 | 32 | |
| 欧拉特征数 | F=60, E=120, V=32 (χ=-28) | |
| 组成与布局 | ||
| 面的种类 | 60个领结形 | |
| 对称性 | ||
| 对称群 | Ih, [5,3], *532 | |
| 特性 | ||
| 等面、非凸 | ||
| 图像 | ||
| ||
性质
编辑大十二面二十面六十面体由60个面、120条边和32个顶点组成[2][3],是一种六十面体。 其具有互相相交的面,是一种复杂多面体,其不仅面与面互相相交,且所有面也都是边自我相交的复杂多边形[2]。
面的组成
编辑大十二面二十面六十面体的面由60个全等的领结形组成,每个领结形彼此互相相交,每个领结形只露出了两侧外部的锐角,其余部分隐没在立体内部。露在该立体外部的部分如下图,以蓝色表示,其中黑线代表领结形彼此互相相交的位置:
| 领结形在立体中的位置 |
领结形是一种反平行四边形,其具有两对边等长的特性[4],因此组成大十二面二十面六十面体的领结形有两种长度的边。若大十二面二十面六十面体对应的对偶多面体之边长为单位长,则大十二面二十面六十面体的短边长为[5]:
长边长为:
长边和短边的比为黄金比例。
由此可以得到其内侧的角约为81.8度:
完全露在立体外部的外侧角约为30度:
领结形两相交之边的交角约为67.7度:
二面角
编辑大十二面二十面六十面体的所有二面角皆相等,约为127.7度[5]:
对偶多面体
编辑根据对偶多面体的定义,多面体的对偶多面体其面将会是原始多面体的顶点图,[6]而大十二面二十面六十面体共有两种顶点,分别为10个领结形的公共顶点,顶点图为十角星、以及6个领结形的公共顶点,这两种顶点分别对应对偶多面体的十角星面和六边形面,因此大十二面二十面六十面体是一种由十角星和六边形组成的多面体,为大十二面二十面体[7],这种立体外观与大双三角十二面截半二十面体类似,差别在于大十二面二十面体比大双三角十二面截半二十面体的凹陷处,凹陷得更深[8]:156。
参考文献
编辑- ^ Eric W. Weisstein. Great Dodecicosacron is the Dual of the Great Dodecicosahedron.. 密歇根州立大学图书馆. 1999-05-25.
- ^ 2.0 2.1 great dodecicosacron. bulatov.org. [2023-02-23]. (原始内容存档于2023-02-23).
- ^ great dodecicosacron. gratrix.net. [2023-02-27]. (原始内容存档于2021-04-01).
- ^ Bryant, John; Sangwin, Christopher J., 3.3 The Crossed Parallelogram, How round is your circle? Where Engineering and Mathematics Meet, Princeton University Press: 54–56, 2008, ISBN 978-0-691-13118-4.
- ^ 5.0 5.1 Versi-Quasi-Regular Duals: Great Dodecicosacron. dmccooey.com. [2023-02-23]. (原始内容存档于2023-02-23).
- ^ Weisstein, Eric W. (编). Dual Polyhedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Great Dodecicosahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Wenninger, M.J. Polyhedron Models. Cambridge University Press. 1974 [2021-09-05]. ISBN 9780521098595. LCCN 69010200. (原始内容存档于2021-08-31).
参考书目
编辑- Wenninger, Magnus, Dual Models, Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 0730208