学生t-分布
学生t分布(Student's t-distribution),简称t 分布,在概率论及统计学中用于根据小样本来估计总体呈正态分布且标准差未知的期望。若总体标准差已知,或是样本数足够大时(依据中心极限定理渐进正态分布),则应使用正态分布来进行估计。其为对两个样本期望差异进行显著性测试的学生t检验之基础。
|
概率密度函数  | |||
|
累积分布函数 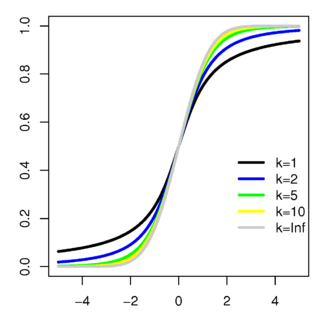 | |||
| 参数 | 自由度 | ||
|---|---|---|---|
| 值域 | |||
| 概率密度函数 | |||
| 累积分布函数 | 其中:是超几何函数 | ||
| 期望 | 时为,时未定义 | ||
| 中位数 | |||
| 众数 | |||
| 方差 | 时为,否则为无穷大 | ||
| 偏度 | 时为 | ||
| 峰度 | 时为 | ||
| 熵 |
| ||
| 矩生成函数 | 未定义 | ||
| 特征函数 |
| ||
学生t 检验改进了Z检验(Z-test),因为在小样本中,Z检验以总体标准差已知为前提,Z检验用在小样本会产生很大的误差,因此必须改用学生t 检验以求准确。但若在样本数足够大(普遍认为超过30个即足够)时,可依据中心极限定理近似正态分布,以Z检验来求得近似值,
在总体标准差数未知的情况下,不论样本数量大或小皆可应用t检验。在待比较的数据有三组以上时,因为误差无法被压低,此时可以用方差分析(ANOVA)代替t检验。
t 分布的推导最早由德国大地测量学家弗里德里希·罗伯特·赫尔默特于1876年提出,并由德国数学家雅各布·鲁洛斯证明。[1][2]
英国人威廉·戈塞于1908年再次发现并发表了t分布,当时他还在爱尔兰都柏林的吉尼斯啤酒酿酒厂工作。酒厂虽然禁止员工发表一切与酿酒研究有关的成果,但允许他在不提到酿酒的前提下,以笔名发表t 分布的发现,所以论文使用了“学生”(Student)这一笔名。之后t检定以及相关理论经由罗纳德·费希尔发扬光大,为了感谢戈塞的功劳,费希尔将此分布命名为学生t 分布(Student's t)。[3]
描述
编辑假设 是呈正态分布的独立的随机变量(随机变量的期望为 ,总体方差为 但其值未知)。 令:
为样本期望,
为样本方差,
为呈期望为0方差为1的正态分布的随机变量,但因总体方差 为未知,因此依斯卢茨基定理以 替换之:
T 的概率密度函数是:
等于n − 1。 T的分布称为t 分布。参数 一般被称为自由度。
是伽玛函数。 如果 是偶数,
如果 是奇数,
T 的概率密度函数的形状类似于期望为0方差为1的正态分布,但更低更宽。随着自由度 的增加,则越来越接近期望为0方差为1的正态分布。
T分布的概率累计函数,用不完全贝塔函数I表示:
其中
T分布的矩为:
学生t 分布置信区间的推导
编辑假设数量A在当T呈t-分布(T的自由度为n − 1)满足
这与
- 是相同的
A是这个概率分布的第95个百分点
那么
等价于
因此μ的90%置信区间为:
计算
编辑现在最方便的计算T分布的办法是使用电子表格软件(如Excel)或查相关在线计算网站。例如,Excel的TDIST(x,v,sides)用来计算自由度为v的T分布,如果第三个参数为1,则给出Pr(T>x);如果第三个参数为2,则计算Pr(T>x Or T<-x).
下表列出了自由度为 的t 分布的单侧和双侧区间值。例如,当样本数量n=5时,则自由度 =4,我们就可以查找表中以4开头的行。该行第5列值为2.132,对应的单侧值为95%(双侧值为90%)。这也就是说,T小于2.132的概率为95%(即单侧),记为Pr(−∞ < T < 2.132) = 0.95;同时,T值介于-2.132和2.132之间的概率为90%(即双侧),记为Pr(−2.132 < T < 2.132) = 0.9。
这是根据分布的对称性计算得到的,
- Pr(T < −2.132) = 1 − Pr(T > −2.132) = 1 − 0.95 = 0.05,
因此,
- Pr(−2.132 < T < 2.132) = 1 − 2(0.05) = 0.9.
注意关于表格的最后一行的值:自由度为无限大的t-分布和正态分布等价。
| 单侧 | 75% | 80% | 85% | 90% | 95% | 97.5% | 99% | 99.5% | 99.75% | 99.9% | 99.95% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 双侧 | 50% | 60% | 70% | 80% | 90% | 95% | 98% | 99% | 99.5% | 99.8% | 99.9% |
| 1 | 1.000 | 1.376 | 1.963 | 3.078 | 6.314 | 12.71 | 31.82 | 63.66 | 127.3 | 318.3 | 636.6 |
| 2 | 0.816 | 1.061 | 1.386 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 14.09 | 22.33 | 31.60 |
| 3 | 0.765 | 0.978 | 1.250 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | 7.453 | 10.21 | 12.92 |
| 4 | 0.741 | 0.941 | 1.190 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 5.598 | 7.173 | 8.610 |
| 5 | 0.727 | 0.920 | 1.156 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 4.773 | 5.893 | 6.869 |
| 6 | 0.718 | 0.906 | 1.134 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 | 4.317 | 5.208 | 5.959 |
| 7 | 0.711 | 0.896 | 1.119 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 4.029 | 4.785 | 5.408 |
| 8 | 0.706 | 0.889 | 1.108 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 | 3.833 | 4.501 | 5.041 |
| 9 | 0.703 | 0.883 | 1.100 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 3.690 | 4.297 | 4.781 |
| 10 | 0.700 | 0.879 | 1.093 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 3.581 | 4.144 | 4.587 |
| 11 | 0.697 | 0.876 | 1.088 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 | 3.497 | 4.025 | 4.437 |
| 12 | 0.695 | 0.873 | 1.083 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 | 3.428 | 3.930 | 4.318 |
| 13 | 0.694 | 0.870 | 1.079 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 3.372 | 3.852 | 4.221 |
| 14 | 0.692 | 0.868 | 1.076 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 | 3.326 | 3.787 | 4.140 |
| 15 | 0.691 | 0.866 | 1.074 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 3.286 | 3.733 | 4.073 |
| 16 | 0.690 | 0.865 | 1.071 | 1.337 | 1.746 | 2.120 | 2.583 | 2.921 | 3.252 | 3.686 | 4.015 |
| 17 | 0.689 | 0.863 | 1.069 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3.222 | 3.646 | 3.965 |
| 18 | 0.688 | 0.862 | 1.067 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.197 | 3.610 | 3.922 |
| 19 | 0.688 | 0.861 | 1.066 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.174 | 3.579 | 3.883 |
| 20 | 0.687 | 0.860 | 1.064 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.153 | 3.552 | 3.850 |
| 21 | 0.686 | 0.859 | 1.063 | 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.135 | 3.527 | 3.819 |
| 22 | 0.686 | 0.858 | 1.061 | 1.321 | 1.717 | 2.074 | 2.508 | 2.819 | 3.119 | 3.505 | 3.792 |
| 23 | 0.685 | 0.858 | 1.060 | 1.319 | 1.714 | 2.069 | 2.500 | 2.807 | 3.104 | 3.485 | 3.767 |
| 24 | 0.685 | 0.857 | 1.059 | 1.318 | 1.711 | 2.064 | 2.492 | 2.797 | 3.091 | 3.467 | 3.745 |
| 25 | 0.684 | 0.856 | 1.058 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.078 | 3.450 | 3.725 |
| 26 | 0.684 | 0.856 | 1.058 | 1.315 | 1.706 | 2.056 | 2.479 | 2.779 | 3.067 | 3.435 | 3.707 |
| 27 | 0.684 | 0.855 | 1.057 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.057 | 3.421 | 3.690 |
| 28 | 0.683 | 0.855 | 1.056 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.047 | 3.408 | 3.674 |
| 29 | 0.683 | 0.854 | 1.055 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.038 | 3.396 | 3.659 |
| 30 | 0.683 | 0.854 | 1.055 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.030 | 3.385 | 3.646 |
| 40 | 0.681 | 0.851 | 1.050 | 1.303 | 1.684 | 2.021 | 2.423 | 2.704 | 2.971 | 3.307 | 3.551 |
| 50 | 0.679 | 0.849 | 1.047 | 1.299 | 1.676 | 2.009 | 2.403 | 2.678 | 2.937 | 3.261 | 3.496 |
| 60 | 0.679 | 0.848 | 1.045 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 2.915 | 3.232 | 3.460 |
| 80 | 0.678 | 0.846 | 1.043 | 1.292 | 1.664 | 1.990 | 2.374 | 2.639 | 2.887 | 3.195 | 3.416 |
| 100 | 0.677 | 0.845 | 1.042 | 1.290 | 1.660 | 1.984 | 2.364 | 2.626 | 2.871 | 3.174 | 3.390 |
| 120 | 0.677 | 0.845 | 1.041 | 1.289 | 1.658 | 1.980 | 2.358 | 2.617 | 2.860 | 3.160 | 3.373 |
| 0.674 | 0.842 | 1.036 | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | 2.807 | 3.090 | 3.291 |
范例
编辑给定一个样本:样本期望和方差分别为10和2,样本大小为11(自由度为10)。根据公式:
可知,使用该方法统计出来的最大值,平均有90%的概率(即90%置信度/置信水平/confidence level)低于:
同理,使用该方法统计出来的最小值,平均有90%的概率(即90%置信度/置信水平/confidence level)高于:
因此,使用该方法统计出来的最大值和最小值,平均有80%的概率介于:
两值之间。(需注意此非代表数据的真正期望介于这两个值之间的概率为80%,详情请参见置信区间。)
参见
编辑参考文献
编辑- ^ Pfanzagl, J.; Sheynin, O. A forerunner of the t-distribution (Studies in the history of probability and statistics XLIV). Biometrika. 1996, 83 (4): 891–898. MR 1766040. doi:10.1093/biomet/83.4.891.
- ^ Sheynin, O. Helmert’s work in the theory of errors. Arch. Hist. Exact Sci. 1995, 49: 73–104. doi:10.1007/BF00374700.
- ^ Moore, David S. Introduction to the Practice of SATISTICS. George P. McCabe, Bruce A. Craig 7th International Edition. New York: W. H. Freeman and Company. 2012: p. 401. ISBN 978-1-4292-8664-0 (英语).
外部链接
编辑- (en)Probability, Statistics and Estimation(页面存档备份,存于互联网档案馆) 首先第112页。













![{\displaystyle {\begin{matrix}{\frac {\nu +1}{2}}\left[\psi ({\frac {1+\nu }{2}})-\psi ({\frac {\nu }{2}})\right]\\[0.5em]+\log {\left[{\sqrt {\nu }}B({\frac {\nu }{2}},{\frac {1}{2}})\right]}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10a24f6de51905e2cbc5b0d4cdae5b1fa7049352)



