司徒頓t分布
司徒頓t分佈(Student's t-distribution),簡稱t 分佈,在機率論及統計學中用於根據小樣本來估計總體呈正態分佈且標準差未知的期望值。若總體標準差已知,或是樣本數足夠大時(依據中心極限定理漸進正態分佈),則應使用正態分佈來進行估計。其為對兩個樣本期望值差異進行顯著性測試的司徒頓t檢驗之基礎。
|
機率密度函數  | |||
|
累積分佈函數 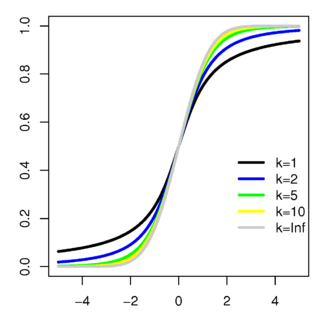 | |||
| 參數 | 自由度 | ||
|---|---|---|---|
| 值域 | |||
| 機率密度函數 | |||
| 累積分佈函數 | 其中:是超幾何函數 | ||
| 期望值 | 時為,時未定義 | ||
| 中位數 | |||
| 眾數 | |||
| 變異數 | 時為,否則為無窮大 | ||
| 偏度 | 時為 | ||
| 峰度 | 時為 | ||
| 熵 |
| ||
| 動差母函數 | 未定義 | ||
| 特徵函數 |
| ||
司徒頓t 檢驗改進了Z檢驗(Z-test),因為在小樣本中,Z檢驗以總體標準差已知為前提,Z檢驗用在小樣本會產生很大的誤差,因此必須改用司徒頓t 檢驗以求準確。但若在樣本數足夠大(普遍認為超過30個即足夠)時,可依據中心極限定理近似正態分佈,以Z檢驗來求得近似值,
在總體標準差數未知的情況下,不論樣本數量大或小皆可應用t檢驗。在待比較的數據有三組以上時,因為誤差無法被壓低,此時可以用方差分析(ANOVA)代替t檢驗。
t 分佈的推導最早由德國大地測量學家弗里德里希·羅伯特·赫爾默特於1876年提出,並由德國數學家雅各布·魯洛斯證明。[1][2]
英國人威廉·戈塞於1908年再次發現並發表了t分佈,當時他還在愛爾蘭都柏林的吉尼斯啤酒釀酒廠工作。酒廠雖然禁止員工發表一切與釀酒研究有關的成果,但允許他在不提到釀酒的前提下,以筆名發表t 分佈的發現,所以論文使用了「司徒頓」(Student)這一筆名。之後t檢定以及相關理論經由羅納德·費雪發揚光大,為了感謝戈塞的功勞,費雪將此分佈命名為司徒頓t 分佈(Student's t)。[3]
描述
編輯假設 是呈正態分佈的獨立的隨機變量(隨機變量的期望值為 ,總體方差為 但其值未知)。 令:
為樣本期望值,
為樣本方差,
為呈期望值為0方差為1的正態分佈的隨機變量,但因總體方差 為未知,因此依史拉斯基定理以 替換之:
T 的機率密度函數是:
等於n − 1。 T的分佈稱為t 分佈。參數 一般被稱為自由度。
是伽瑪函數。 如果 是偶數,
如果 是奇數,
T 的機率密度函數的形狀類似於期望值為0方差為1的正態分佈,但更低更寬。隨着自由度 的增加,則越來越接近期望值為0方差為1的正態分佈。
T分佈的機率累計函數,用不完全貝塔函數I表示:
其中
T分佈的矩為:
司徒頓t 分佈置信區間的推導
編輯假設數量A在當T呈t-分佈(T的自由度為n − 1)滿足
這與
- 是相同的
A是這個機率分佈的第95個百分點
那麼
等價於
因此μ的90%置信區間為:
計算
編輯現在最方便的計算T分佈的辦法是使用電子表格軟件(如Excel)或查相關線上計算網站。例如,Excel的TDIST(x,v,sides)用來計算自由度為v的T分佈,如果第三個參數為1,則給出Pr(T>x);如果第三個參數為2,則計算Pr(T>x Or T<-x).
下表列出了自由度為 的t 分佈的單側和雙側區間值。例如,當樣本數量n=5時,則自由度 =4,我們就可以查找表中以4開頭的行。該行第5列值為2.132,對應的單側值為95%(雙側值為90%)。這也就是說,T小於2.132的機率為95%(即單側),記為Pr(−∞ < T < 2.132) = 0.95;同時,T值介於-2.132和2.132之間的機率為90%(即雙側),記為Pr(−2.132 < T < 2.132) = 0.9。
這是根據分佈的對稱性計算得到的,
- Pr(T < −2.132) = 1 − Pr(T > −2.132) = 1 − 0.95 = 0.05,
因此,
- Pr(−2.132 < T < 2.132) = 1 − 2(0.05) = 0.9.
注意關於表格的最後一行的值:自由度為無限大的t-分佈和正態分佈等價。
| 單側 | 75% | 80% | 85% | 90% | 95% | 97.5% | 99% | 99.5% | 99.75% | 99.9% | 99.95% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 雙側 | 50% | 60% | 70% | 80% | 90% | 95% | 98% | 99% | 99.5% | 99.8% | 99.9% |
| 1 | 1.000 | 1.376 | 1.963 | 3.078 | 6.314 | 12.71 | 31.82 | 63.66 | 127.3 | 318.3 | 636.6 |
| 2 | 0.816 | 1.061 | 1.386 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 14.09 | 22.33 | 31.60 |
| 3 | 0.765 | 0.978 | 1.250 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | 7.453 | 10.21 | 12.92 |
| 4 | 0.741 | 0.941 | 1.190 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 5.598 | 7.173 | 8.610 |
| 5 | 0.727 | 0.920 | 1.156 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 4.773 | 5.893 | 6.869 |
| 6 | 0.718 | 0.906 | 1.134 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 | 4.317 | 5.208 | 5.959 |
| 7 | 0.711 | 0.896 | 1.119 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 4.029 | 4.785 | 5.408 |
| 8 | 0.706 | 0.889 | 1.108 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 | 3.833 | 4.501 | 5.041 |
| 9 | 0.703 | 0.883 | 1.100 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 3.690 | 4.297 | 4.781 |
| 10 | 0.700 | 0.879 | 1.093 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 3.581 | 4.144 | 4.587 |
| 11 | 0.697 | 0.876 | 1.088 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 | 3.497 | 4.025 | 4.437 |
| 12 | 0.695 | 0.873 | 1.083 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 | 3.428 | 3.930 | 4.318 |
| 13 | 0.694 | 0.870 | 1.079 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 3.372 | 3.852 | 4.221 |
| 14 | 0.692 | 0.868 | 1.076 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 | 3.326 | 3.787 | 4.140 |
| 15 | 0.691 | 0.866 | 1.074 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 3.286 | 3.733 | 4.073 |
| 16 | 0.690 | 0.865 | 1.071 | 1.337 | 1.746 | 2.120 | 2.583 | 2.921 | 3.252 | 3.686 | 4.015 |
| 17 | 0.689 | 0.863 | 1.069 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3.222 | 3.646 | 3.965 |
| 18 | 0.688 | 0.862 | 1.067 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.197 | 3.610 | 3.922 |
| 19 | 0.688 | 0.861 | 1.066 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.174 | 3.579 | 3.883 |
| 20 | 0.687 | 0.860 | 1.064 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.153 | 3.552 | 3.850 |
| 21 | 0.686 | 0.859 | 1.063 | 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.135 | 3.527 | 3.819 |
| 22 | 0.686 | 0.858 | 1.061 | 1.321 | 1.717 | 2.074 | 2.508 | 2.819 | 3.119 | 3.505 | 3.792 |
| 23 | 0.685 | 0.858 | 1.060 | 1.319 | 1.714 | 2.069 | 2.500 | 2.807 | 3.104 | 3.485 | 3.767 |
| 24 | 0.685 | 0.857 | 1.059 | 1.318 | 1.711 | 2.064 | 2.492 | 2.797 | 3.091 | 3.467 | 3.745 |
| 25 | 0.684 | 0.856 | 1.058 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.078 | 3.450 | 3.725 |
| 26 | 0.684 | 0.856 | 1.058 | 1.315 | 1.706 | 2.056 | 2.479 | 2.779 | 3.067 | 3.435 | 3.707 |
| 27 | 0.684 | 0.855 | 1.057 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.057 | 3.421 | 3.690 |
| 28 | 0.683 | 0.855 | 1.056 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.047 | 3.408 | 3.674 |
| 29 | 0.683 | 0.854 | 1.055 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.038 | 3.396 | 3.659 |
| 30 | 0.683 | 0.854 | 1.055 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.030 | 3.385 | 3.646 |
| 40 | 0.681 | 0.851 | 1.050 | 1.303 | 1.684 | 2.021 | 2.423 | 2.704 | 2.971 | 3.307 | 3.551 |
| 50 | 0.679 | 0.849 | 1.047 | 1.299 | 1.676 | 2.009 | 2.403 | 2.678 | 2.937 | 3.261 | 3.496 |
| 60 | 0.679 | 0.848 | 1.045 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 2.915 | 3.232 | 3.460 |
| 80 | 0.678 | 0.846 | 1.043 | 1.292 | 1.664 | 1.990 | 2.374 | 2.639 | 2.887 | 3.195 | 3.416 |
| 100 | 0.677 | 0.845 | 1.042 | 1.290 | 1.660 | 1.984 | 2.364 | 2.626 | 2.871 | 3.174 | 3.390 |
| 120 | 0.677 | 0.845 | 1.041 | 1.289 | 1.658 | 1.980 | 2.358 | 2.617 | 2.860 | 3.160 | 3.373 |
| 0.674 | 0.842 | 1.036 | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | 2.807 | 3.090 | 3.291 |
範例
編輯給定一個樣本:樣本期望值和方差分別為10和2,樣本大小為11(自由度為10)。根據公式:
可知,使用該方法統計出來的最大值,平均有90%的機率(即90%置信度/置信水平/confidence level)低於:
同理,使用該方法統計出來的最小值,平均有90%的機率(即90%置信度/置信水平/confidence level)高於:
因此,使用該方法統計出來的最大值和最小值,平均有80%的機率介於:
兩值之間。(需注意此非代表數據的真正期望值介於這兩個值之間的機率為80%,詳情請參見置信區間。)
參見
編輯參考文獻
編輯- ^ Pfanzagl, J.; Sheynin, O. A forerunner of the t-distribution (Studies in the history of probability and statistics XLIV). Biometrika. 1996, 83 (4): 891–898. MR 1766040. doi:10.1093/biomet/83.4.891.
- ^ Sheynin, O. Helmert’s work in the theory of errors. Arch. Hist. Exact Sci. 1995, 49: 73–104. doi:10.1007/BF00374700.
- ^ Moore, David S. Introduction to the Practice of SATISTICS. George P. McCabe, Bruce A. Craig 7th International Edition. New York: W. H. Freeman and Company. 2012: p. 401. ISBN 978-1-4292-8664-0 (英語).
外部連結
編輯- (en)Probability, Statistics and Estimation(頁面存檔備份,存於互聯網檔案館) 首先第112頁。













![{\displaystyle {\begin{matrix}{\frac {\nu +1}{2}}\left[\psi ({\frac {1+\nu }{2}})-\psi ({\frac {\nu }{2}})\right]\\[0.5em]+\log {\left[{\sqrt {\nu }}B({\frac {\nu }{2}},{\frac {1}{2}})\right]}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10a24f6de51905e2cbc5b0d4cdae5b1fa7049352)



