岁差

关于物理学描述的进动，请见“进动”。

岁差，又称地轴进动（英语：axial precession），是指某一天体的自转转轴指向在其他天体的引力的作用下，相对于空间中的惯性坐标系所发生的缓慢且连续的变化。地球的岁差主要由太阳、月球及其他行星作用在地球赤道隆起部分的引力矩引起。在天文和大地测量学中，岁差一般专指地球自转轴缓慢且均匀的变化，周期约25,722年。其他周期较短或不规律的变化则被称为章动。

岁差的运动方向（顺时针）与地球的自转方向（逆时针）相反。

岁差（P）、章动（N）与地球自转（R）的示意图，图中黑色实直线为地球自转轴，虚线为黄轴

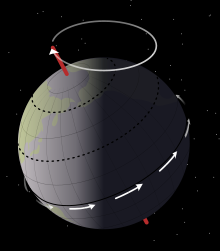
岁差的具体表现是地球赤道面和黄道面的变化，这两种变化又分别被称为赤道岁差和黄道岁差。赤道岁差的影响主要表现为春分点以每年约51″的速率连续向西运动。这种影响能够通过回归年与恒星年之间的差异，以及北天极和北极星相对位置的变化被直接观察到。黄道岁差的影响则表现为春分点以每年约0.1″的速率向东移动，以及黄赤交角的缓慢变化。赤道岁差与黄道岁差又被统称为总岁差（英语：general precession）。

岁差的名称和含义随历史的发展而变化。历史上，古希腊天文学家喜帕恰斯首先发现了春分点在黄道上的移动，提出了分点岁差（英语：the precession of the equinoxes）一词。汉语中的“岁差”则出自于《宋书·历下》记载的“冬至所在，岁岁微差”，意为每年冬至点的位置存在着微小的差别。在相当长的一段时间内，分点岁差曾是岁差的唯一含义。随着计算精度的提升，天文学家于19世纪上半叶发现了其他行星对黄道面的影响。最早在1863年，行星岁差（英语：planetary precession）一词就被提出，用于与因太阳与月球引力而形成的日月岁差（英语：lunisolar precession）相区别，。二者同样被合称作总岁差，以逐渐取代过去的“分点岁差”。在行星对赤道面的影响没有被发现之前，“行星岁差”和“黄道岁差”曾被视作同义词，“日月岁差”则和“赤道岁差”亦是如此。随着测量和计算精度的进一步提升，行星引力对赤道面的影响变得无法忽视。为避免造成误解，国际天文联合会在2006年将“日月岁差”和“行星岁差”分别重新命名为当前使用的“赤道岁差”和“黄道岁差”。

岁差影响地球的自转轴、春分点和黄赤交角，从而影响人类对深空及近地空间的观测，甚至是地球的气候。在大地测量学中，岁差和章动、极移以及日长变化又被统称为地球定向参数。

作用

地球自转轴的进动有许多可以观测到的作用。首先，天极南极和北极的位置相对于看起来是固定的背景星空有移动的现象，完成一周的时间大约是25,771.5年（依据2000年的速率）。因此，现在靠近天球北极被称为北极星的恒星，会随着时间的迁移，其它的恒星将成为“北极星” 。当天极移动时，从地球这个特定的位置观察，这种在星场中指向的移动是以同位角逐渐进行的。

其次，地球环绕太阳轨道的分点和至点的位置，或其他相对于季节定义的时间，也在缓慢的改变。例如，假设地球在轨道的夏至位置时，地轴的指向的倾斜是朝向太阳。在完整的绕行一圈后，太阳相对于背景的恒星回到了相同的视位置，但地轴指向的倾斜却不是朝向太阳：由于岁差的作用，它稍微超越了这一个点。换句话说，夏至在轨道上的位置提早了一些。因此，回归年，意思是季节的周期(例如，从至点至至点，或从分点至分点)是比恒星年，这是以太阳相对于恒星的视位置来测量的，短了约20分钟。注意这每一年20分钟的差，大约经过25,771.5年，累积的量就相当于一年，所以在经过25,771.5年之后，极轴对应在轨道上的位置又“回到当它的开始”。（事实上，其它的作用也会慢慢的改变地球轨道的形状和方向，并且和岁差作用结合在一起，创造出各种不同的变化；参考米兰科维奇循环。地轴倾角的大小，而不是只有指向，也会随着时间慢慢的变化，但这种作用不能直接归咎于进动。）

因此，太阳的视位置在相同季节的固定时间的背景恒星，好比说春分点，也会以每年50.3秒（大约是360度除以25,771.5），或是每71年一度的速率，在传统的12个黄道带星座之间缓缓的退行完整的360°。

历史

中国

《太初历》斗初斗三18h13m45.8s<26.25>牵牛初冬至19h57m15.2s<46>危十六度立春22h58m36.6s

《四分历》斗初箕三18h24m10.3s<21.25>斗二十一度八分冬至19h47m57.0s<45.65625>危十度二十一分立春22h47m57.0s

斗初移-2.64003038日，冬至移2.35975174日，立春移2.70386458日

AD85.12 计立春，七十年得岁差一日

《景初历》没法967/67315，黄帝至四分历(AD85)=1843+208=2051年，岁差29.463225(近1个月)，亦即AD237后1900年累积，至1个月才移前作调整

东晋虞喜是发现并研究岁差现象的第一位中国天文学家，东晋咸和五年（330年），他计算出冬至太阳位置每50年向西移动一度（现代测定为71年零8个月），当时把这种现象描述“岁差”，意即“太阳位置每岁有差”，认识到这是一种周期性天体运动现象、原因不明。

南北朝时期，祖冲之（429年－500年）测定创制大明历，其中写到：“冬至所在，岁岁微差”，首次纳入岁差计算，后正式创造“岁差”一词 。

公元600年，隋朝天文学家刘焯（zhuo）创《皇极历》，并用“二次插值公式”来计算日、月、五星的运行速度。这一计算公式，比西欧的牛顿、泰勒等早提出1千年，并在其后唐朝高度发达的天文学测量与计算中，帮助中国古代天文学家逐渐掌握了岁差计算的规律。

巴比伦人

20世纪以来的西欧学者认为，许多种不同的文化也都以各自的论述独立发现喜帕恰斯所谓的岁差，例如，有一种观点认为巴比伦人已经知到岁差。

依据阿尔巴坦尼(Al-Battani)的说法，巴比伦天文学家已经区分出恒星年和回归年(岁差值就是这回归年和恒星年之间的差异)。他阐明大约在公元前330年，他们已经估计出恒星年的长度是S_K = 365日6小时11分(= 365.258日)误差大约是28分钟。在1923年施纳贝尔(P. Schnabel)主张大约在公元前315年的西丹努斯(Kidinnu)的理论与岁差有关。奥托纽格包尔(Otto Neugebauer)在1950年代就此问题所做的工作支持施纳贝尔(和更早期的Kugler)巴比伦人发现岁差的理论。

在最近的几十年中，这个假说在de Santillana和von Dechend的著作哈姆雷特的基石中被再生放大（Harvard University Press, 1969）。从极端的Panbabylonism到考古天文学，他们推荐巴比伦神话故事中的岁差，引起了即使远至中国、波里尼西亚、和北美洲的世界地区，也有类似的神话在扩散。虽然他们的理论并未在学术界被广泛的接受，但预期岁差考古天文学会引起大众的兴趣在近期流行。

古埃及

在喜帕恰斯提出岁差之前的古埃及，也有相似的论述，但这些仍有争议。在一些卡奈克神庙复杂的建筑中，据称在一年当中的关键时刻，某些特定的恒星会从未经证实的点所指向的地平线方向升起或落下。几个世纪后，岁差使这些指向失去了时效，而且这些神庙重建过。虽然，对正恒星方向错误的增加并不表示埃及的观测者不知道恒星会以每72年一度的速率在天空中移动。然而，他们保留了精确的日历法，而如果纪录了庙宇重建的日期，那么绘制出粗略的岁差速率是非常简单的事。黄道十二星座浮雕，来自丹德拉的哈托尔神庙星图在时间上比托勒密的时代晚，据称纪录了岁差（Tompkins 1971）。无论如何，如果古埃及人知道岁差，他们的知识没有被纪录在现存的天文文件内。

迈克尔赖斯的著作《埃及的传统》（英语：Egypt's Legacy），"虽然不能知道，岁差在公元前2世纪被喜帕恰斯定义之前，古埃及人是否知道岁差的机制，但是有专人监视夜晚星空的他们不可能不知道这种作用。" (p. 128) 。赖斯相信"对岁差的基本了解应该是推动埃及进展的动力" (p. 10)，在某种意义上，"作为一个民族国家的埃及和埃及王的国王被视为是活的神，天文上的变化与无穷尽天体的视运动，包括岁差，被认为是埃及人实现的产品" (p. 56)。追随着卡尔·古斯塔夫·荣格( Carl Gustav Jung)，赖斯说道："来自吉萨金字塔很精密的对准基点的证据，显示在公元前第三个千禧年的埃及(并且可能还在这个日期之前)就已经有很纯熟的天文观测技术，可以很精密的对准至所需要的恒星。单只这一个事实久足以使荣格相信埃及人对岁差的知识有着很好的认识，而不是一种凑巧的巧合。" (p. 31) 赖斯继续说：The Egyptians also, says Rice, were "当原本设计对向的恒星因为岁差改变了位置，埃及人也会修改庙宇的方向，在新的国王即位时，这种现象似乎发生过许多次。" (p. 170)

古埃及菁英的祭司追踪岁差周期数千年之久的概念在与罗伯特·鲍威尔(Robert Bauval)和葛瑞姆·汉卡克 (Graham Hancock)于1966年著作的《创世纪的守护神》（英语：Keeper of Genesis）这本书中扮演着中心理论被详细的阐明。作者声称古埃及人建造的巨大建筑是投影天空中的地图，同时与其相关的仪式是尘世代理天体事件的精心制作。特别的是，仪式象征的"回头(turning back)"抵达的源头时间是岁差周期所谓的Zep Tepi ("起点")，根据作者的计算，大约是公元前10,500年。

玛雅文明

有着推测的中美洲长数日历以某种方式反复的校准岁差，但是这些观点并未获得玛雅文明的预言专家的支持。

印度

主条目：Ayanamsa

一份12世纪的文件，Bhāskar II说："依据Suryasiddhanta，在一Kalpa(43亿2千万年)中，sampāt反转了30,000次，同时说在一个Kalpa中Munjāla向前移了199,669，并且一个要合并这两个，还要弄清楚倾斜之前，和上升的差异，等等"。兰斯洛特金森翻译了诗篇的最后三个章节，简明扼要的表达出完整的意义，并且跳过了一部分的组合以现代印度语的评述带出合并这两个之前的。依据印度语的评述，岁差周期的最后数值应该是结合ayana的+199,669转和sampaat的-30,000转，得到每Kalpa+169,669；也就是25,461年一个周期，这与现在的25,771年很接近。

此外，Munjāla的数值给了ayana 运动的周期是21,636年，这是现代将近点岁差也加入计算所得到的岁差数值。后者(ayana)在现在的周期是1,360,000年，但在Bhāskar II钟给他的数值是144,000年(每Kalpa30,000)T，并称之为sampāt。Bhāskar-II没有给结合负值的sampāt和正值的ayana之后的最后项目一个名称，但是他给ayana的值显示这是轨道和近点的进动两者共同影响组合的岁差值，并且sampāt的意义就是近点周期，但把它定义成分点。他的言词是有点混淆，但它澄清是从它自己的Vāsanābhāshya评述Siddhānta Shiromani，并不是说Suryasiddhanta这本古籍在他写传闻证据的基础上不可靠。Bhāskar-II没有给它本身的见解，他只是引用了Suryasiddhanta、Munjāla 和其他未命名的。

根据传统的评论，现存的Suryasiddhanta支持在±27°范围内每年54"的抖动，但伯吉斯(Burgess)引用Bhāskar-II所提及的Suryasiddhanta，认为原始的意义应该是一个循环的运动。

西欧的中世纪和文艺复兴

在中古伊斯兰天文学中，于马拉盖天文台汇编的《伊儿汗历表》（Zij-i Ilkhani）给出的分点岁差是每年51弧秒，与现在的数值50.2弧秒非常接近。

在中世纪，伊斯兰教和拉丁的基督教天文学家都认为恒星的“抖动”是加诸于岁差的一种运动。这种理论通常归功于阿拉伯天文学家塔比·伊本·库拉，但现代社会已经对此一归属提出异议。尼古拉·哥白尼在他著作的《天体运行论》（1543年）对这种抖动给了不同的解释，这项工作第一次明确提到岁差是地球自转轴运动的结果。哥白尼将岁差的特性作为地球的第三种运动。可见最早到1543年，欧洲人才认识到岁差现象的真实成因。

喜帕恰斯的发现

岁差的发现通常被归功于喜帕恰斯，一个据说是罗德岛或是伊兹尼克的希腊天文学家。喜帕恰斯介绍了他在至点和分点移动上的发现(天文学大成 III.1和VII.2的叙述)。他在月食的时侯测量角宿一的黄道经度，发现大约在秋分点的西方6°。经由比较自己和亚历山大的提默洽里斯(他与阿里斯基尔都是与欧几里得同时期的公元前3世纪早期的学者)，他发现在150年前的角宿一经度少了约2°，他也注意到其它的恒星也有相同的运动，他推测在黄道带上的恒星位置会随着时间改变。托勒密称这是"第一假设" (天文学大成 VII.1)，但是没有提出更多可能是喜帕恰斯已经制定的假设。喜帕恰斯显然限制他的思考，因为他只依据几个旧的观测，而这些也不是很可靠的。

为何喜帕恰斯需要在月食的时刻测量恒星的位置呢？因为二分点的位置不会标示在天空中，所以他需要以月球作为位置的参考。喜帕恰斯已经制定了一种方法可以算出任何时间的太阳经度。月食只会在满月，月球与太阳冲的时刻发生。在食的中心时刻，月球与太阳的经度精确的相差180度。喜帕恰斯认为测量角宿一与月球在弧度上的经度差。以这个数值，加上计算所得的太阳经度，再加上180°就是月球的经度；他以相同的过程处理提默洽里斯的数据(Evans 1998, p. 251)。顺便提一下，观察相同的食，是喜帕恰斯获得工作上所需要数据的主要来源，由于有关他生平的资料非常稀少，他观测过的月食，例如公元前146年4月21日和公元前135年3月21日(Toomer 1984, p. 135 n. 14)。

喜帕恰斯也以年的长度来研究岁差。在他的工作中，他了解有两种年的长度。回归年是从地球的角度看太阳回到黄道(太阳在天球上的群星间经过的路径)上同一位置所花费的时间长度。恒星年是太阳回到天球上同一颗恒星位置所经历的时间长度。岁差造成恒星的经度每年都会有些微的改变，所以恒星年比回归年稍为长了一点。对分点和至点的观察，喜帕恰斯发现回归年的长度是365+1/4−1/300 日，或365.24667日(Evans 1998, p. 209)。与恒星年一年的长度比较，他计算岁差在一个世纪中不会少于1°。从这些资料，它计算出恒星年长度可能的数值是365+1/4+1/144日(Toomer 1978, p. 218)，通过给与最小的误差可能率，他已经将观测允许的误差考虑进去。 经由修改默冬和卡利布斯(Callippus)的闰日和闰月(已经失传)，喜帕恰斯以接近他的回归年长度创造了自己的阴阳历，如同托勒密在天文学大成 III.1所述说的(Toomer 1984, p. 139)。从公元前499年起，巴比伦历使用19年235个阴历月的历法(在公元前380年之前只有3个例外)，但是它没有指定一个月的日数。默冬章(432 BC)在19年中有6,940日，倒置一年的平均日数是365+1/4+1/76日或365.26316日。卡利布斯周期( 330 BC)比4个默冬章(76年)少了一日，因此一年的平均是365+1/4或365.25日。喜帕恰斯在4个卡利布斯周期(304年)中在减少一日，创造了喜帕恰斯周期，一年的平均长度是365+1/4−1/304或365.24671日，这与回归年的长度365+1/4−1/300或365.24667日非常接近。这三种希腊的历法周期都未曾用于任何的民用历中 － 他们只出现在天文学大成这一份天文的文件中。

我们发现喜帕恰斯的数学特征出现安提基特拉机械，公元前2世纪古老的天文计算机。这个机器依据的周期有太阳年、默冬章，这是月球以相同的相位出限在天空中同一颗恒星位置的时间(满月大约每19年出现在天空中相同的位置)，卡利布斯周期(他是4个默冬章并且更准确)、沙罗周期和转轮期(3沙罗周期，更准确的预测日食)。对安提基特拉机械的研究证明古代人基于太阳和月球在天空中的各方面的运动，一直使用很准确的日历。事实上，安提基特拉机械的一部分描述了月球的运动和相位，是阴历的机制，对某一给定的时间，以一列串联起来的4个齿轮，以针和插槽的设备，使月球的速度变化非常接近开普勒第二定律，也就是，他得到月球在近地点的运动速度较快，在远地点的运动速度较慢的计算值。此一发现证明喜帕恰斯的数学是比托勒密在他的书中所叙述的更为进步，很明显的他发展了与开普勒第二定律非常好的近似。

托勒密

根据《天文学大成》（1496年版）一书，一千二百年前的托勒密是注意到岁差现象的第二位天文学家。托勒密使用喜帕恰斯测量月球变化的方法，不需要利用日时，测量了轩辕十四、角宿一和其它亮星的经度。在日落之前，他先测量月球和太阳分离的经度，然后在日落之后，他测量月球至恒星的弧长。他用喜帕恰斯的模型计算太阳的经度，并且利用月球的运动和视差做出修正(Evans 1998, pp. 251–255)。托勒密将它自己的观测和喜帕恰斯、亚力山卓的梦尼劳斯、提默洽里斯和亚基帕的做比较。他发现从喜帕恰斯到他自己的年代(大约265年)，恒星已经移动了2°40'，或是每百年1° (每年36"；现在认可的速率是每年大约50"，或是72年1°)。他也证实岁差不只是影响靠近黄道的恒星，而是影响到所有的恒星，并且他找到的周期和喜帕恰斯一样，都是36,000年。

其它古希腊天文著作

许多古老的著作都没有提到岁差，或许是不知道的缘故。除了托勒密之外，这份清单还包括普洛克拉斯(Proclus)，他否认岁差，和亚力山卓的赛昂( Theon of Alexandria )，他在四世纪评论托勒密，并且接受托勒密的解释。赛昂也提供一种理论供选择：

根据某些古代占星学家的看法相信从某一个特定的时期夏至的标示依照标示的顺序移动了8°，之后它们会退回相同的数值. . . . (Dreyer 1958, p. 204)

取代完整的绕行黄道带序列的程序，分点只是在8°的弧度内反复的前进和后退。这种trepidation的理论是赛昂当时提出对岁差的另一种选择。

另外现代学者研究表明，虽然证据上仍有争议，但或许古希腊的西蒙的阿利斯塔克斯时就能区分恒星年和回归年。

拜火教的问题

参见：密特拉和密特拉教

拜火教(Mithraism)是一种神秘的宗教或是基于火神崇拜的学校。许多的地下庙宇大约都在公元前1世纪至公元5世纪的罗马帝国时期建立。因为缺乏书面的文件或经籍，要了解拜火教有相当的困难；教学必须要经由发现的插图（来自曾经当过拜火教会众聚会场所的地下洞穴，且有黄道带和相关标帜的浮雕）重建后才能进行。直到1970年代，大多数的学者跟随着佛兰兹居蒙(Franz Cumont)一起确认密斯拉(Mithras)是波斯的火神(Mithra)。居蒙的论点在1971年被重新调查，并且相信密斯拉是只受到波斯宗教轻微影响的综摄神。

拜火教被公认为明显的具有占星学的元素，但是细节仍要讨论。一位拜火教的学者，David Ulansey，曾经解释密斯拉(密斯拉太阳是打不倒的勇者－不可战胜的太阳)是第二个太阳或是造成岁差的恒星。他认为这种崇拜是受到喜帕恰斯发现岁差的启发而兴起的。他的分析一部分建立在tauroctony的星图，密斯拉用公牛献祭的图像。密斯拉是第二个太阳或超宇宙太阳；或是星座就是英仙座，而公牛就是黄道带上的星座，金牛座。在更早的占星术年代，太阳经过的春分点位置落在金牛座，由于这个原因，以密斯拉-柏修斯纪念"金牛时期"的结束（大约在公元前2000年在春分点，或是公元前11,500年在秋分点）。

插画还包含在黄道带的两侧拿着两只火炬标帜的男孩(Cautes and Cautopates)。Ulansey和Walter Cruttenden在他们的书中失去的时间和神秘的恒星(Lost Star of Myth and Time)，解释这意味着年龄的增长和老化，或是光明和黑暗；宇宙进展的原始元素。因此，拜火教被认为在岁差周期或大年（分点的进动完整绕行一周的柏拉图年）的纪元变化中会有所动作。

近代

在人造卫星和电子计算机建立出更精确的岁差模型以前，被普遍接受的岁差数值是西蒙·纽康于19世纪末计算得到的结果。他计算得到的总岁差的经度分量（以 $p$ 表示）为每回归世纪5,025.64弧秒。1976年，美国天文学家 Jay H. Lieske 将 $p$ 更新为每儒略世纪5,029.0966弧秒。VLBI和LLR等现代技术的出现，使岁差的数值能被更精确地测定。国际天文联合会在2000年采用了新的常数，又于2003年和2006年采用了新的计算方法和多项式以对岁差进行表达。累积岁差的计算公式为：

$p_{A}=5\,028.796\,195T+1.105\,434\,8T^{2}+O(T^{3})$

单位为每儒略世纪弧秒，$T$为自2000.0分点起算的儒略世纪数(儒略世纪为36,525天)。

对累积岁差进行求导，得到岁差的速率为：

$p=5\,028.796\,195+2.210\,869\,6T+O(T^{2})$

以这个常数项推算的岁差周期为25,772年。

在17世纪，艾萨克·牛顿在他的自然哲学的数学原理 (1687)一书中也用万有引力 Evans 1998, p. 246)来解释岁差。然而，牛顿原始的进动方程不能正常的工作（顺利的解出答案），经由后起之秀的科学家让·勒朗·达朗伯特大幅修订才得以完成。

在1825年，乔治·居维叶(Baron Georges Cuvier)引用Jean Baptiste Delambre的工作估计 page 163 完整的周期是25,960年，这是以大约在公元1800年测量的结果与喜帕恰斯比较。与目前所接受的数值比较，差异略大于0.5%。

影响

地轴运动在天球上的投影，蓝线表示平天极在天球上的运动，红线表示春分点在黄道上的运动，二者的方向和速率是相同的

岁差是赤道岁差和黄道岁差综合作用的结果。其中，赤道岁差可看作是赤道面相对于黄道面的运动。在这一描述下，黄道坐标系被视为不变的参考系，而赤道坐标系则被视为以每年约50.39''绕北黄极以顺时针的方向（即向西）旋转，周期约为25,722年。定义于赤道坐标系的所有结构，包括天极与分点，都处在同样的运动当中。天极的漂移会影响极星的选择，分点的漂移会使分点落于不同的星座内，而赤纬的漂移会影响同一恒星和星座的可见性。

极点的漂移

主条目：极星

天极是地球自转轴在天球上的投影，极星则是天球上最靠近天极的恒星。极星的变化是作为赤道坐标系基点的天极运动的结果。天极在绕北黄极旋转时，逐次经过不同的恒星，因此不同时代的极星会各不相同。当前，北极星是小熊座内视星等为2.0等的勾陈一；而在公元前约3,000年，北极星是天龙座内视星等为3.67等的右枢；而到公元14,000年左右，北极星将会变为天琴座内的零等星织女一。由于岁差近似于周期性运动，到约25,722年后，勾陈一将再次成为北极星。

极点的漂移还使得同样的恒星在不同时代下的赤纬发生变化，从而影响其在同一地区的可见性。例如，由于自古希腊时期到当代，南天极正逐渐向南十字座移动，使得南十字座的赤纬逐渐减小，对于北半球的亚热带地区落入了恒隐圈内。因此，对于希腊及其同纬度的地区，如今要找到这个星座变得更为困难。

值得注意的是，由于交角岁差的存在，黄极相对于恒星背景也并非固定不变。而且，恒星本身也存在着自行运动。因此，在经过25,722年的周期后，相对于遥远的恒星背景，天极的位置和与地球较近的恒星的位置较上一周期也会有微小的变化。

带时间刻度的外部线显示了在公元前48,000年至公元52,000年的时间间隔内，地球北极在历元J2000.0的固定天空上的进动路径的投影。内侧线显示了在相同时间间隔内地球轨道北极的进动路径投影。内侧线显示了在相同时间间隔内地球轨道北极的进动路径投影。白色加号表示不变平面的北极的方向，青色网格表示黄道坐标系，黄色表示历元J2000.0的赤道坐标系。这些恒星的亮度都比5等星亮

。

春分点相对于恒星背景向西（图中为右方）移动，在过去6,000年内依次经过金牛座（Taurus）、白羊座、双鱼座（Pisces）

分点的漂移

主条目：黄道十二宫

分点是黄道与赤道的两个交点，包括春分点和秋分点。其中，春分点在天文学中常作为赤经和黄经坐标的起点，在占星学中又作为黄道十二宫的第一点。分点的漂移表现为在黄道上的”退行“，即向西移动，其速度同样为每年约50.39''。在黄道十二宫形成时的新巴比伦王朝时期，春分点位于白羊座内，白羊宫因此成为了黄道十二宫的第一宫。由于岁差的影响，现在的春分点相比当时已有约37°的移动，处在双鱼座内。这一移动明显地表现在天文学和占星学中，太阳在黄道星座以及与其对应的黄道星宫中的时间的不同。例如，以中气点等分定义的白羊宫，其对应的时间于每年的3月21日左右开始，而实际上太阳是在每年的4月18日左右才进入天文学上的白羊座。每一星座被春分点落入的时段又被称为“大月（英语：Great Months）”，近三个“大月”的时间分别是：

星座	起始	结束
金牛座	4500 BC	2000 BC
白羊座	2000 BC	100 BC
双鱼座	100 BC	2700 AD

分点的移动还表现为，恒星年与回归年的差异。其中，恒星年是地球连续两次经过恒星背景中的一点的时间间隔，回归年是地球连续两次经过春分点的时间间隔。由于春分点的退行，地球在公转时相对于恒星背景中的同一点，会稍早地抵达下一个春分点，使得回归年比恒星年约短20分24秒。

对气候的影响

主条目：米兰科维奇循环

右边的图在以北半球来说明相对于近日点和远日点的轴向进动作用，分点岁差控制了气候的周期性变化，也就是所熟知的米兰科维奇循环。

注意在图上特定季节扫掠过的面积会随着时间改变，轨道力学要求季节长度需要与对应季节的象限被扫掠过的面积成比率，所以在轨道离心率的极值，在远心点上的时间(日期)会比在近心点上要长。今天，在北半球，在秋季与冬季位于近日点附近，地球以最快的速度运动着，因此冬季和秋季比春季和夏季为短。现在，北半球的夏天比冬天长4.66天，春天比秋天长2.9天。轴向进动缓缓的改变地球的分点与至点在轨道上的位置，参考回归年有更详细的说明与数值。在未来的10,000年，北半球的冬季会逐渐变长，而夏季会变得短些，最后，创造出来的环境将顺理成章的引发下一次的冰河期。

成因

分点岁差是太阳和月球对地球的引力造成的，其它天体也有少许的作用。此一解释最早是由牛顿提出的 轴向进动类似陀螺的进动。在这两种状况，作用力都是引力。对陀螺，这种力几乎平行于自转轴。但是对地球，这种力来自太阳和月球，几乎垂直于自转轴。

地球不是一个理想的球体，而是一个扁球体，在赤道的直径比两极的直径长了43公里。因为地球的轴倾，导致在一整年中几乎有一半突起的部分，向南或向北分别偏离中心朝向太阳，或朝相反的方向偏离中心。因为引力随着距离增加而减弱，接近的这一半受到较强的引力，这使得太阳拉扯地球的一侧比另一侧更困难，因而对地球产生一个小小的扭力。这个扭矩轴大致垂直于地球的自转轴，所以转轴产生了进动。如果地球是一个理想的球，就不会有进动。

这个平均转矩是垂直于自转轴且倾向远离黄极的方向，因此并不会改变轴本身的倾斜。来自太阳(或月球)的扭矩大小会随着引力和地球的旋转轴对齐的方向而改变，当正交的时候趋近于零。

尽管上述的解释都与太阳有关，同样的解释适用于绕着地球运动的任何天体，值得注意的是沿着或靠近黄道的天体，特别是月球。太阳和月球结合的行动称为日月岁差。除了由太阳和月球造成的稳定前行运动(完成一个完整的圆大约25,700年)，还会造成小位置的变化。这种振荡，包括进动的速度和轴倾，被称为章动。最重要的项目只有18.6年的周期和小于20弧秒的振幅。 除了日月岁差之外，太阳系内其他的行星也造成黄道整体沿着测量时的瞬时黄经174° 附近的轴缓慢的转动，这种行星岁差的值每年在黄道上的移动量只有0.47角秒(不到日月岁差值的百分之一)。这两种岁差的总和就是我们一般所认知的综合岁差。

方程

由太阳、月球或是行星对地球造成的潮汐力。

在地球上的潮汐力是由平方反比定律的天体（太阳、月球或行星）引力摄动造成的结果，即造成摄动的天体施加在地球近侧的引力大于远侧的引力。如果摄动天体的引力施加于地球的中心(等于离心力)是减除了摄动天体施加于地球表面各处的引力，留下的就是潮汐力。对进动，这种潮汐力形成两种力但只作用在球从极到极之间的赤道隆起。这个力偶可以分解成两对元件，一对平行于地球的赤道平面，分别朝向和远离摄动的天体，并且相互抵消；另一对平行于地球的自转轴，两者都朝向赤道平面。后面这一对创造出下述的扭矩矢量 ：

${\overrightarrow {T}}={\frac {3Gm}{r^{3}}}(C-A)\sin \delta \cos \delta {\begin{pmatrix}\sin \alpha \\-\cos \alpha \\0\end{pmatrix}}$

此处

Gm = 摄动天体的标准引力参数

r = 摄动天体的地心距离

C = 围绕地球自转轴转动的转动惯量

A = 任何环绕地球赤道直径的转动惯量

C−A = 地球赤道隆起的转动惯量(C>A)

δ = 摄动天体的赤纬 (赤道以南或北)

α = 摄动天体的赤经 (从春分点向东)

扭矩在地球中心的(从上到下)的3个单位矢量x是在黄道面上(在黄道平面上的方向是沿着黄道和赤道的交点)指向春分点，y在黄道面上指向夏至点(x的东方90°)，和z指向黄道的北极点。

对于太阳的三个正弦曲线项目在x方向的数值(sinδ cosδ sinα)是正弦平方波的形式，数值的变化从在分点(0°, 180°)的0到至点(90°, 270°)的0.36495。太阳在y方向(sinδ cosδ (−cosα))的数值在四个分至点是从0至±0.19364(稍微超过正弦平方波一半的数值)，在分点和至点中间的峰值位置稍微偏离中间(分别在43.37°(−), 136.63°(+), 223.37°(−), 316.63°(+))。太阳的照两个波形从波峰到波峰的振幅相同，并且有相同的周期，都是公转周期的一半或是半年。在z方向的数值为0。

无论是月球或太阳，正弦波形的平均扭矩在y方向的值为0，所以在这个方向的扭矩不会影响到进动。对太阳或月球，正弦平方波的平均扭矩在x方向的运动是：

$T_{x}={\frac {3}{2}}{\frac {Gm}{a^{3}(1-e^{2})^{3/2}}}(C-A)\sin \epsilon \cos \epsilon$

此处

$a$ = 地球(太阳)或月球的轨道半长轴

e =地球(太阳)或月球的轨道离心率

和正弦平方波形平均1/2计算值，$a^{3}(1-e^{2})^{3/2}$整个椭圆轨道的地球到太阳或月球平均距离的立方，和 $\epsilon \,\!$ (黄道面和赤道面的夹角)是太阳在赤道上能达到的δ(赤纬)最大值，并且是月球在18.6年的完整周期内的平均最大值。

进动是：

${\frac {d\psi }{dt}}={\frac {T_{x}}{C\omega \sin \epsilon }}$

此处ω是地球的角速度，和Cω是地球的角动量。因此由太阳导致进动的第一阶成分是：

${\frac {d\psi _{S}}{dt}}={\frac {3}{2}}\left[{\frac {Gm}{a^{3}(1-e^{2})^{3/2}}}\right]_{S}\left[{\frac {(C-A)}{C}}{\frac {\cos \epsilon }{\omega }}\right]_{E}$

而月球的是：

${\frac {d\psi _{L}}{dt}}={\frac {3}{2}}\left[{\frac {Gm(1-1.5\sin ^{2}i)}{a^{3}(1-e^{2})^{3/2}}}\right]_{L}\left[{\frac {(C-A)}{C}}{\frac {\cos \epsilon }{\omega }}\right]_{E}$

此处的i是月球轨道面和黄道面的夹角。在这两个方程，太阳的参数在标示为S的方括弧内，月球的参数在标示为L的方括弧内，地球的参数在标示为E的方括弧内。这个项目$(1-1.5\sin ^{2}i)$计算月球轨道相对于黄道的倾角，项目(C−A)/C是地球的力学椭率或扁率，因为地球内部的结构不清楚，知道的也不够详尽，因此需要观测到的岁差来调整。如果地球是均值的，这个项目将等于第三阶偏心角 。

$e''^{2}={\frac {\mathrm {a} ^{2}-\mathrm {c} ^{2}}{\mathrm {a} ^{2}+\mathrm {c} ^{2}}}$

此处的a 是赤道半径(6378137 m)，和c是极半径(6356752 m)，所以e'' ²=0.003358481.

应用的参数是J2000.0舍入到7位有效数字(不包含前导的1)是：

太阳	月球	地球
Gm=1.3271244×1020 m³/s²	Gm=4.902799×1012 m³/s²	(C−A)/C=0.003273763
$a$=1.4959802×1011 m	$a$=3.833978×108 m	ω=7.292115×10−5 rad/s
e=0.016708634	e=0.05554553	$\epsilon \,\!$=23.43928°
	i= 5.156690°

此处给与

dψ_S/dt = 2.450183×10⁻¹² /s

dψ_L/dt = 5.334529×10⁻¹² /s

两个的值都必须转换成"/a (弧秒/年)，以2π弪度量(1.296×10⁶"/2π)的数值和在每年(儒略年)秒的数值(3.15576×10⁷s/a)：

dψ_S/dt = 15.948788"/a   vs   15.948870"/a 取自威尔士

dψ_L/dt = 34.723638"/a   vs   34.457698"/a 取自威尔士

因为地球的轨道是完整的椭圆，因此太阳的方程能很好的描述出由太阳造成的进动，只有受到其他行星微小的摄动。月球的方程就不能很好的描述月球进动的形式，因为他的轨道受到太阳很大的扭曲。

数值

岁差的变率不是一个常数，因为在线性(和高阶的)项目中的T，是随着时间逐渐增加的。无论如何必须强调的是这个公式只适用在在有限的时间内，可以很清楚的看出，如果T够大(就是说在够久的未来或过去)，则T²将成为主导，p的数值将变得非常大。实际上，对太阳系的数值模型更精确的计算显示，岁差的常数有大约41,000年的周期，类似黄道的倾斜。要注意此处提到的常数是在线性和高阶的公式上，而非岁差的本身。也就是说：

p = A + BT + CT² + … 只是下面公式的近似 p = A + Bsin (2πT/P)，此处P 是410个世纪的周期。

理论上的模型也许计算岁差(p)在时间(T)上的高次项，但是因为无止尽的多项式可以转化成周期函数，当T够大时（无论是正或负）都会趋向无穷大。基于这种动机下，国际天文联合会选择了最容易开发和利用的理论。在未来或之前的几个世纪，所有的公式都不会导出无穷大的数值；在未来或过去的数千年，都能维持在一定的准确度内；在更长的时间中，误差变得太大，甚至在一个岁差周期内，岁差的确切变率和期间都变得难以计算。

地球的轴心岁差是一个缓慢的效应，但在天文学家工作所需要的精确度上，每天的变化都需要被考虑到。要注意，虽然岁差和轴的倾斜（对黄道面的倾角）是从相同的理论推算出来的，并且彼此有关联性，但两者的运动是各自独立的，是在互相垂直的方向上运动。

在更长的时间周期内，也就是百万年的岁月中，岁差看来是有25,700年的类似周期，但是，他不会这样保持下去。根据沃德的推论，月球的距离因为潮汐的作用在持续的增加中。在未来的15亿年，当从现在的60.3增加至66.5地球半径，来自行星共振的效应，将会先使岁差的周期延长至49,000年；在大约20亿年时，月球的距离达到68地球半径，岁差周期也将变成69,000年。这将与轴在黄道上倾角大幅的变动相关联。然而，沃德在潮汐的散逸上使用了异于寻常的新派的数值，在6.2亿年的平均时间，使用潮汐节奏一半大的值，但是这种同步共振大约要30至40亿年才能达到，而在这个时间之前许久（大约从现在开始21亿年后），由于太阳光度的增加，地球上的海水早就沸腾而消失了，势必大幅改变潮汐的作用。

黄经总岁差与交角岁差

岁差常数

在2003年前，国际上通行的岁差模型是由国际天文联合会确定的IAU1976模型（又称L77模型）。在该模型中，岁差被分为黄经总岁差和交角岁差，黄经总岁差描述的是春分点的移动在黄经上的分量，而交角岁差描述的是黄赤交角的变化。在与IAU1976模型同时确定的IAU1976天文常数系统中，黄经总岁差的速率 $p$ 和历元J2000.0时刻的黄赤交角 $\epsilon _{0}$分别为：

$p=5\,029.0\,965''/{\text{c}}\pm 0.3''/{\text{c}}$

$\epsilon _{0}=84\,381.412''\pm 0.005''$

在国际地球自转服务（IERS）提供的IERS2003规范中，黄经总岁差和交角岁差的值被更新为：

$p=5\,038.478\,75''/{\text{c}}\pm 0.000\,40''/{\text{c}}$

$\epsilon _{0}=84\,381.405\,9''\pm 0.000\,3''$

在2009年以后，随着这一模型不再被IERS使用，黄经总岁差的速率现已不再作为天文常数的一部分被IAU发布。

数值计算

在IAU1976模型中，黄经总岁差和交角岁差相对于历元J2000.0的数值计算公式分别为：

$p_{A}=5\,029.096\,6''t+1.111\,61t^{2}-0.000\,113t^{3}$

$\epsilon _{A}=\epsilon _{0}-46.815\,0''t-0.000\,59t^{2}+0.001\,813t^{3}$

其中， $t$ 的单位为一个儒略世纪，即36525个儒略日。值得注意的是，上述常数和数值计算公式只是在某段有限的时间内对岁差的线性逼近，只在距离初始历元较小（即 $t$ 较小时）才会有较好的近似。

改正

天球坐标系以地球自转轴指向的天极为基点，地轴朝向的变化使得在不同时刻定义出的天球坐标系存在细微的差别。岁差改正的目的就是将观测目标在瞬时平天球坐标系下的坐标归化到某一指定时刻的协议天球坐标系（CIS）中。假设在时刻 $t_{i}$，观测到目标的瞬时平天球坐标为 $\mathbf {r} (t_{i})$，且其在定义于 $t_{0}$ 时刻的协议天球坐标为 $\mathbf {r} (t_{0})$，则两个坐标可以通过下式进行转换：

$\mathbf {r} (t_{0})=\left[\mathbf {P} (t_{i},t_{0})\right]\mathbf {r} (t_{i})$

其中，$P(t_{i},t_{0})$被称为岁差矩阵。

岁差改正是地球定向模型的一部分，也是国际天球参考框架（ICRF）和国际地球参考框架（ITRF）间相互转换的环节之一。从2003年1月1日起，国际天文联合会（IAU）开始采用MHB2000模型来为两个框架提供转换参数，这一模型给出了岁差矩阵$P(t_{i},t_{0})$的具体形式。

三次坐标旋转法

MHB2000模型使用了三个欧拉角来表示转换前后的坐标系的相对位置，并将岁差矩阵表达为三个旋转矩阵的乘积：

$\left[\mathbf {P} (t_{i},t_{0})\right]=\mathbf {R_{Z}} (\eta _{A})\mathbf {R_{Y}} (-\theta _{A})\mathbf {R_{Z}} (\zeta _{A})$

其中，$\zeta _{A}$、$\theta _{A}$和$\eta _{A}$即为三个欧拉角。除了得出岁差矩阵的数值表示以外，上式还表达了瞬时平天球坐标系转换为协议天球坐标系的具体步骤：

1. 将瞬时天球坐标系的X轴从瞬时平春分点移开，绕瞬时平天球坐标系的Z轴（即沿瞬时赤道面）逆时针旋转$\zeta _{A}$角，得到第一过渡坐标系；
2. 将第一过渡坐标系的X轴绕其Y轴（即沿子午圈）顺时针旋转$\theta _{A}$角，得到第二过渡坐标系，此时第二过渡坐标系的Z轴和赤道面与协议天球坐标系的重合；
3. 将第二过渡坐标系的X轴绕协议天球坐标系的Z轴（即沿协议天球坐标系的赤道面）逆时针旋转$\eta _{A}$角，使其与协议天球坐标系的春分点重合，此时整个坐标系与协议天球坐标系重合。

四次坐标旋转法

由于ICRF定义的自转轴与MHB2000模型所采用的自转轴并非完全一致，传统的时间多项式难以简洁地表达三次坐标旋转法中使用的欧拉角$\zeta _{A}$和$\eta _{A}$。Capitaine等人提出了以四次坐标旋转法表达岁差矩阵的方式。与三次坐标旋转法类似，四次坐标旋转法将岁差矩阵表达为四个旋转矩阵的乘积：

$\left[\mathbf {P} (t_{i},t_{0})\right]=\mathbf {R_{X}} (-\epsilon _{0})\mathbf {R_{Z}} (\psi _{A})\mathbf {R_{X}} (\omega _{A})\mathbf {R_{Z}} (-\chi _{A})$

其中，$\chi _{A}$、$\omega _{A}$、$\psi _{A}$和$\epsilon _{0}$即为四个旋转角。该式同样给出了岁差矩阵的数值表示和转换的具体步骤：

1. 将瞬时天球坐标系的X轴从瞬时平春分点移开，绕瞬时平天球坐标系的Z轴（即沿瞬时赤道面）顺时针旋转$\chi _{A}$角，得到第一过渡坐标系；
2. 保持第一过渡坐标系的X轴不变，将其赤道面绕其X轴逆时针旋转$\omega _{A}$角，得到第二过渡坐标系，此时第二过渡坐标系的赤道面的协议天球坐标系的黄道面重合；
3. 将第二过渡坐标系的X轴绕其Z轴（即沿协议天球坐标系的黄道面）逆时针旋转$\psi _{A}$角，得到第三过渡坐标系，此时第三过渡坐标系的X轴与协议天球坐标系的春分点重合；
4. 保持第三过渡坐标系的X轴不变，将其赤道面绕其X轴顺时针旋转$\epsilon _{0}$角，此时整个坐标系与协议天球坐标系重合。

在由国际地球自转服务（IERS）提供的IERS2010规范中，使用的岁差模型是由国际天文联合会给出的IAU2006岁差模型（英语：IAU 2006 precession）。上述的四个旋转角在这一模型中被表达为时间的五次多项式：

• $\chi _{A}=10.556\,403\,00''t-2.381\,429\,200''t^{2}-0.001\,211\,970\,0''t^{3}+0.000\,170\,663\,00''t^{4}-0.000\,000\,056\,000''t^{5}$
• $\omega _{A}=\epsilon _{0}-0.025\,754\,00''t+0.051\,262\,300''t^{2}-0.007\,725\,030\,0t^{3}-0.000\,000\,467\,00t^{4}+0.000\,000\,333\,700t^{5}$
• $\psi _{A}=5\,038.481\,507\,00t-1.079\,006\,900t^{2}-0.001\,140\,45t^{3}+0.000\,132\,851\,00t^{4}-0.000\,000\,095\,100t^{5}$
• $\epsilon _{0}=84\,381.406''$

其中，$\epsilon _{0}$ 又为历元J2000.0下定义的协议天球坐标系的黄赤交角， $t$ 是当前历元相对于历元J2000.0的儒略世纪数。

相关条目

• 转轴倾角
• 尤拉角
• 米兰科维奇循环
• 章动
• 恒星年

参考书籍

• Explanatory supplement to the Astronomical ephemeris and the American ephemeris and nautical almanac
• Precession and the Obliquity of the Ecliptic has a comparison of values predicted by different theories
• A.L. Berger (1976), "Obliquity & precession for the last 5 million years", Astronomy & astrophysics 51, 127
• J.H. Lieske et al. (1977), "Expressions for the Precession Quantities Based upon the IAU (1976) System of Astronomical Constants （页面存档备份，存于互联网档案馆）". Astronomy & Astrophysics 58, 1..16
• W.R. Ward (1982), "Comments on the long-term stability of the earth's obliquity", Icarus 50, 444
• J.L. Simon et al. (1994), "Numerical expressions for precession formulae and mean elements for the Moon and the planets", Astronomy & Astrophysics 282, 663..683
• N. Capitaine et al. (2003), "Expressions for IAU 2000 precession quantities （页面存档备份，存于互联网档案馆）", Astronomy & Astrophysics 412, 567..586
• J.L. Hilton et al. (2006), "Report of the International Astronomical Union Division I Working Group on Precession and the Ecliptic （页面存档备份，存于互联网档案馆）" (pdf, 174KB). Celestial Mechanics and Dynamical Astronomy (2006) 94: 351..367
• Rice, Michael (1997), Egypt's Legacy: The archetypes of Western civilization, 3000-30 BC, London and New York.
• Dreyer, J. L. E.. A History of Astronomy from Thales to Kepler. 2nd ed. New York: Dover, 1953.
• Evans, James. The History and Practice of Ancient Astronomy. New York: Oxford University Press, 1998.
• Pannekoek, A. A History of Astronomy. New York: Dover, 1961.
• Parker, Richard A. "Egyptian Astronomy, Astrology, and Calendrical Reckoning." Dictionary of Scientific Biography 15:706-727.
• Tomkins, Peter. Secrets of the Great Pyramid. With an appendix by Livio Catullo Stecchini. New York: Harper Colophon Books, 1971.
• Toomer, G. J. "Hipparchus." Dictionary of Scientific Biography. Vol. 15:207-224. New York: Charles Scribner's Sons, 1978.
• Toomer, G. J. Ptolemy's Almagest. London: Duckworth, 1984.
• Ulansey, David. The Origins of the Mithraic Mysteries: Cosmology and Salvation in the Ancient World. New York: Oxford University Press, 1989.
• Schütz, Michael: Hipparch und die Entdeckung der Präzession. Bemerkungen zu David Ulansey, Die Ursprünge des Mithraskultes, in: ejms = Electronic Journal of Mithraic Studies, www.uhu.es/ejms/Papers/Volume1Papers/ulansey.doc

外部链接

• D'Alembert and Euler's Debate on the Solution of the Precession of the Equinoxes （页面存档备份，存于互联网档案馆） at Convergence （页面存档备份，存于互联网档案馆）