悬链曲面

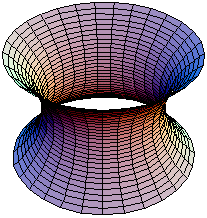
悬链曲面（又名悬垂曲面）是一个曲面，是将悬链线绕其准线旋转而得（见右侧动画），故为一旋转曲面。除了平面以外，悬链曲面也是第一个被发现的极小曲面，在1744年被莱昂哈德·欧拉发现且证明。Jean Baptiste Meusnier也做了些早期的研究。只有两个曲面既为旋转曲面又是最小曲面，即为平面与悬链曲面。 悬链曲面可被以下参数式所定义：

悬链曲面

A catenoid obtained from the rotation of a catenary

将悬链线绕其准线旋转而得的悬链曲面

$x=c\cosh {\frac {v}{c}}\cos u$

$y=c\cosh {\frac {v}{c}}\sin u$

$z=v$

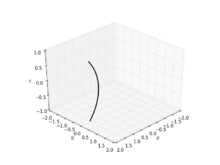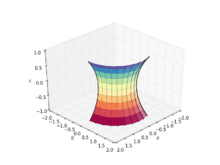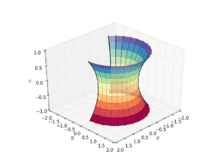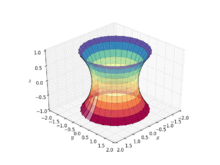
其中$u\in [-\pi ,\pi )$，$v\in \mathbb {R}$且$c$为非零实数。 在圆柱座标系则有：

$\rho =c\cosh {\frac {z}{c}}$

其中$c$为实数。

理想状态下，把一对经过肥皂溶液浸泡的圆形铁环张开，就可以得到一个悬链面形状的肥皂膜。这个现象的原理是由于肥皂膜会趋向于形成在固定边界（铁环）下表面积最小的旋转曲面，根据这个原理，可以用变分法证明肥皂膜的形状是悬链面。

螺旋面变换

此动画展示了螺旋面如何变型成悬链曲面

螺旋面与悬链曲面属同一相关曲面，我们可以在不拉缩的情况下将悬链曲面扳成螺旋面。也就是说，我们可以用一个连续且等距的变换将悬链曲面变成螺旋面的一部分，且在变型的每一瞬间，曲面皆为极小曲面。此变换可由下列式子给出：

$x(u,v)=\cos \theta \,\sinh v\,\sin u+\sin \theta \,\cosh v\,\cos u$

$y(u,v)=-\cos \theta \,\sinh v\,\cos u+\sin \theta \,\cosh v\,\sin u$

$z(u,v)=u\cos \theta +v\sin \theta \,$

注意$(u,v)\in (-\pi ,\pi ]\times (-\infty ,\infty )$，且变换参数$\theta$满足$-\pi <\theta \leq \pi$，

其中 $\theta =\pi$对应到右旋螺旋面， $\theta =\pm \pi /2$对应到悬链曲面， $\theta =0$对应到左旋螺旋面。

该等距变换可以由微分几何中的曲面第一基本形式证明。

参见

• 几何
• 曲面