懸鏈曲面

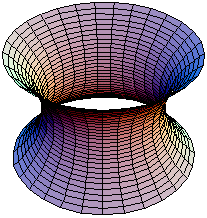
懸鏈曲面（又名懸垂曲面）是一個曲面，是將懸鏈線繞其準線旋轉而得（見右側動畫），故為一旋轉曲面。除了平面以外，懸鏈曲面也是第一個被發現的極小曲面，在1744年被萊昂哈德·歐拉發現且證明。Jean Baptiste Meusnier也做了些早期的研究。只有兩個曲面既為旋轉曲面又是最小曲面，即為平面與懸鏈曲面。 懸鏈曲面可被以下參數式所定義：

懸鏈曲面

A catenoid obtained from the rotation of a catenary

將懸鏈線繞其準線旋轉而得的懸鏈曲面

$x=c\cosh {\frac {v}{c}}\cos u$

$y=c\cosh {\frac {v}{c}}\sin u$

$z=v$

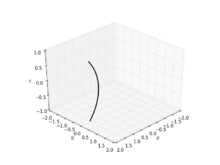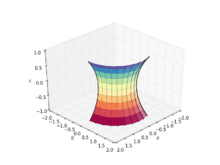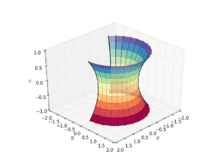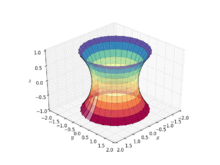
其中$u\in [-\pi ,\pi )$，$v\in \mathbb {R}$且$c$為非零實數。 在圓柱座標系則有：

$\rho =c\cosh {\frac {z}{c}}$

其中$c$為實數。

理想狀態下，把一對經過肥皂溶液浸泡的圓形鐵環張開，就可以得到一個懸鏈面形狀的肥皂膜。這個現象的原理是由於肥皂膜會趨向於形成在固定邊界（鐵環）下表面積最小的旋轉曲面，根據這個原理，可以用變分法證明肥皂膜的形狀是懸鏈面。

螺旋面變換

此動畫展示了螺旋面如何變型成懸鏈曲面

螺旋面與懸鏈曲面屬同一相關曲面，我們可以在不拉縮的情況下將懸鏈曲面扳成螺旋面。也就是說，我們可以用一個連續且等距的變換將懸鏈曲面變成螺旋面的一部份，且在變型的每一瞬間，曲面皆為極小曲面。此變換可由下列式子給出：

$x(u,v)=\cos \theta \,\sinh v\,\sin u+\sin \theta \,\cosh v\,\cos u$

$y(u,v)=-\cos \theta \,\sinh v\,\cos u+\sin \theta \,\cosh v\,\sin u$

$z(u,v)=u\cos \theta +v\sin \theta \,$

注意$(u,v)\in (-\pi ,\pi ]\times (-\infty ,\infty )$，且變換參數$\theta$滿足$-\pi <\theta \leq \pi$，

其中 $\theta =\pi$對應到右旋螺旋面， $\theta =\pm \pi /2$對應到懸鏈曲面， $\theta =0$對應到左旋螺旋面。

該等距變換可以由微分幾何中的曲面第一基本形式證明。

參見

• 幾何
• 曲面