潮汐锁定

海洋学的潮汐共振是另一篇独立的文章。

此条目介绍的是潮汐锁定。关于对地月系统更为定量的描述，请见“潮汐加速”。

潮汐锁定（或同步自转、受俘自转）发生在重力梯度使天体永远以同一面对着另一个天体；例如，月球永远以同一面朝向着地球。潮汐锁定的天体绕自身的轴旋转一圈要花上绕着同伴公转一圈相同的时间。这种同步自转导致一个半球固定不变的朝向伙伴。通常，在给定的任何时间里，只有卫星会被所环绕的更大天体潮汐锁定，但是如果两个天体的物理性质和质量的差异都不大时，各自都会被对方潮汐锁定，这种情况就像冥王星与卡戎。理论上，较小的天体也可以潮汐锁定比自身大数倍的天体，但需要十分长的时间，大多数情况下，在两个天体被摧毁前也无法实现。

潮汐锁定的结果是造成卫星绕轴自转的周期和绕着行星公转的周期有着大约相同的时间。排除天平动的影响，月球会像左图一样，始终用同一面朝向地球（从月球自转轴的上方鸟瞰，并且未依比例绘制）。如果月球没有自转，在它环绕地球公转时，如右图所示，则它的正面和背面会交替地朝向地球。

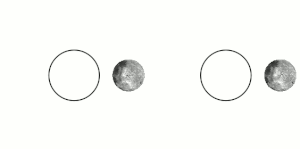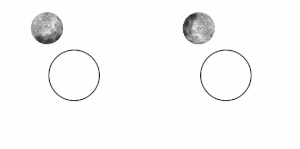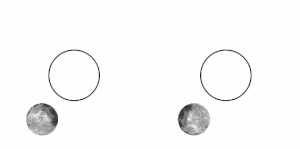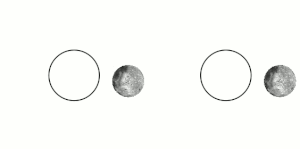
这种效应被使用在一些人造卫星的稳定上。

机制

在自转率的改变上，大的天体A将天体B潮汐锁定，需要A的引力在B的隆起的诱导下造成扭矩。

潮汐隆起

A的引力对B造成潮汐力使得B的引力平衡受到扭曲，形状在朝向A的轴线方向上变得细长；相反的，在垂直A轴向的维度上略有减少。这种扭曲现象被称为潮汐隆起。当B未被潮汐锁定时，这个隆起会在表面移动，两个隆起之一会在靠近A在正上方的一个点。对大型的天体而言，由于本身的重力，形状会接近球体，潮汐的扭曲会造成轻微的扁球体，也就是说一个沿着主轴方向轴对称的椭球体。较小的天体也会经历这种扭曲，但这些扭曲是不规则的。

隆起拖曳

物体B对潮汐力引起的周期性的重塑会施全力（Exertion）的抵抗。事实上，有时候B需要一些时间来重塑重力的平衡，但在这段时间，A-B的轴向因为B的旋转已经改变，所以形成的隆起会与A-B轴向有一段距离。从太空中的瞭望点来看，隆起最高点的方向与指向A的方向已经有了偏差。如果B的自转周期短于它的轨道周期，这个隆起将超前于A-B轴的指向；反过来如果B的自转周期较长，取而代之的是隆起将落后。

扭矩的结果

由于隆起偏离了A-B轴指向的方向，A的引力将拉住这些质量而对B施加了扭矩。在面对A的隆起，扭矩的作用使B的自转符合轨道周期，但在"背面"的隆起是远离A的，因此起了相反的作用（维持自转的周期）。不过，朝向A这一侧的隆起比背面的隆起更靠近A大约相当于B的直径，所以会经历较强的引力和扭矩。来自这两个隆起扭矩的净效应，是永远朝向B的自转周期与轨道周期同步，也就是结果终将是潮汐锁定。

轨道变化

如果自转的频率大于轨道 (公转)频率，抵制的小扭矩将会浮现，最终达成频率锁定（绿色描述的情况）。

A-B系统的总角动量在这个过中是守恒的，所以当B减慢速度和失去角动量时，轨道的角动量会提升相似的量（其中也有一些对A的自转造成较小的影响）。这样的结果是导致B在减缓自转速度时，相对于A的轨道会提升。而另一种情况，当B的自转速度太慢时，潮汐锁定的作用会使它的自转加速，同时使B的轨道降低。

大天体的锁定

潮汐锁定的效应也会发生在大天体A上，只是因为B的体积较小，引力作用也较微弱，所以需要更长的时间才能将A潮汐锁定。例如，地球的自转就因为月球而逐渐减缓，从一些化石在地质时间上的推移可以察觉其总量。 这个过程仍在进行中，而且已经大幅减缓了地球从诞生迄今的自转速度。目前的估计是协助（与太阳的潮汐影响）地球的自转从6个小时至当前的24小时。而在目前的阶段，原子钟显示地球的一天每年大约延长15微秒。只要给予足够的时间，就将在月球和地球创造出相互的潮汐锁定，地球的一天会逐渐延长，而恒星月或逐渐缩短，直到两者有着相同的时间长度。但这个过程是非常缓慢的，不能期望在太阳成为红巨星，吞噬掉地球和月球之前就能发生。

对于大小相似的天体，这种效应在同等级规模的天体上，或许会两者同时被潮汐锁定。矮行星冥王星和它的卫星卡戎就是最好的例子—只有从冥王星的一个半球可以看见卡戎，反之亦然。而冥王星的年龄估计和地球与太阳系内其他的行星大致是相同的。

自转轨道共振

最后，在轨道离心率较高的情况下，潮汐力是相对较弱的，较小的天体最终可能会产生轨道共振而不是潮汐锁定。在这种情况下，轨道周期和自转周期的比率是一些明确但不同于1:1的分数。一个著名的例子是水星的自转 － 锁定到与公转太阳周期为3:2的共振。

许多太阳系外行星（特别是靠近母天体的那些行星）预料将会有高于1:1的自转轨道共振。 例如，超级地球的葛利泽581 d最可能会在2:1的自转轨道共振下，每自转两次绕着母星公转一圈。

事件

卫星

由于潮汐锁定，在中央天体的居民永远看不见标示绿色的一面。

在太阳系中许多值得注意的卫星最值得注意的就是潮汐锁定，因为它们的轨道非常接近，就因为距离的减少，而使潮汐力迅速增加（与距离的三次方成反比）。值得注意的例外是气体巨行星外围的不规则卫星，距离比那些知名的大卫星远了许多。

冥王星和卡戎是潮汐锁定的一个极端例子。与主星相比，卡戎是一颗相对较大的卫星，轨道也非常靠近，使得冥王星也被卡戎潮汐锁定。实际上，这两颗天体彼此相互环绕着（质心位于冥王星外），好像是以一根竿子在两个天体的表面各自固定着一个点而相对着。

小行星卫星是否潮汐锁定，大部分的情况仍属未知，但预期轨道紧密的密接小行星会如同密接联星一样是潮汐锁定的。

月球

因为月球是1:1的潮汐锁定，所以从地球只能看见月球正面的一侧。

月球的自转和轨道周期相互之间是潮汐锁定的，所以无论从地球的何处观察月球，始终只能见到月球同一面的半球。直到1959年，从前苏联航天器月球3号传送回来的照片，才完整的看见月球背面。

尽管月球的自转和公转完全被锁定，但是由于天秤动和视差，从地球反复的观测，仍可以看见月球总表面的大约59%。天秤动主要的成因是月球轨道的离心率造成的轨道速度变化：使地球的观测者在周边上可以多观测到约6°。视差是几何学的效果：是在地球表面上相对于地月中心联线的偏移量，而因为这个关系，使月球在我们的地平线时，可以多观察到一点月球表面的边缘（大约1°）。

行星

天文学家原本认为水星是被太阳潮汐锁定的，这是因为在适合观测水星时，它都以同一面朝向地球的观测者。1959年，雷达观测证明水星是以3:2的轨道共振而非1:1的完全潮汐锁定；即水星每自转3圈就绕着太阳公转2圈。这使得地球上的观测者在适合观测的时间观测时，水星都以同一面朝向着地球，出现它似乎被潮汐锁定的假象。水星的轨道离心率造成稳定的3:2轨道共振。

金星的每583.92天与地球会合一次，几乎是金星自转的5个太阳日（精确的说是5.001444金星日），使得每次接近地球时都以同一侧朝向地球。这种现象是偶然还是与地球的某种潮汐锁定关系，目前仍不得而知。

当一个行星被恒星潮汐锁定时，行星的一侧会是永恒的星光照耀，而另一侧是在永恒的黑暗中。

恒星

整个宇宙的密接联星都被认为是潮汐锁定的，已经被发现轨道极为靠近主星的系外行星也被认为是潮汐锁定的。一个不寻常的例子，MOST卫星已经证实右摄提二（牧夫座τ）被一颗行星潮汐锁定着，并且几乎可以肯定潮汐锁定是相互的。

时间尺度

使用下列的公式可以估算一个天体被潮汐锁定所需要的时间尺度：

$t_{\textrm {lock}}\approx {\frac {wa^{6}IQ}{3Gm_{p}^{2}k_{2}R^{5}}}$

此处

• $\omega \,$是初始的自转速率（弧度每秒弧度）。
• $a\,$是卫星环绕行星运动的半长轴。
• $I\approx 0.4m_{s}R^{2}$是卫星的转动惯量。
• $Q\,$是卫星的散逸函数（消耗函数）。
• $G\,$是万有引力常数。
• $m_{p}\,$是行星的质量。
• $m_{s}\,$是卫星的质量。
• $k_{2}\,$是卫星潮汐的二阶勒夫数
• $R\,$是卫星的半径。

除了地球和月球的$k_{2}/Q=0.0011$之外，一般来说对Q和$k_{2}$的所知都很有限。然而，实务上都粗略的估计Q≈100（或许过于保守，会高估锁定的时间），并且

$k_{2}\approx {\frac {1.5}{1+{\frac {19\mu }{2\rho gR}}}},$

此处

• $\rho \,$是卫星的密度。
• $g\approx Gm_{s}/R^{2}$是卫星的表面重力。
• $\mu \,$是钢体的卫星。对岩石的卫星大约是3×10¹⁰ Nm⁻²，对只是冰冻的卫星大约是4×10⁹ Nm⁻²。

可以看出，即使已经知道卫星的大小和密度，依然留下了许多必需要估计的参数（特别是$\omega$、Q、和$\mu \,$），所以任何对潮汐锁定的计算所获得的时间都不被预期是正确的，甚至会差到10个数量级。更进一步说，在潮汐锁定阶段的轨道半径a可能由于后续的潮汐加速，已经完全不同于当今观测到的，而这个值在潮汐锁定的时间上是很敏感的。

由于不确定性是如此的高，上面的公式可以简化以避免繁琐的计算。假设卫星是球体的，$k_{2}\ll 1\,$，Q = 100，明智的做法是以12小时为间隔去猜测一个未潮汐锁定的初始公转周期（大多数的小行星自转周期在2小时到2天之间）。

$t_{\textrm {lock}}\quad \approx \quad 6\ {\frac {a^{6}R\mu }{m_{s}m_{p}^{2}}}\quad \times 10^{10}\ {\textrm {years}},$

式中的质量单位是公斤，距离单位为米，同时μ是Nm⁻²。对岩石天体μ可以粗略的选择为3×10¹⁰ Nm⁻²，对冰冻天体μ是4×10⁹ Nm⁻²。

请注意与轨道半径a的相关性极强。

在主星和卫星都已经潮汐锁定的状态，例如冥王星，卫星和主星的参数可以互换。

一个结论是，其它的因素不变（像是Q和μ），在同样轨道半径上的大卫星将比小卫星更快的被行星潮汐锁定，因为$m_{s}\,$的成长是卫星半径$R$的三次方。在土星系统中有一个可能的例子，土卫七(Hyperion)未被潮汐锁定，而质量较大且轨道距离较远的土卫八(Iapetus)却已经被锁定。不过还必须要指出这是不明确的，因为土卫七(Hyperion)还受到邻近的土卫六(泰坦)强大的驱动，这会使它的自转造成混乱。

上述公式的锁定时间尺度可能切割了数量级的顺序，因为它们忽略了频率与$k_{2}/Q$的依赖关系。

已知被潮汐锁定天体列表

太阳系

被太阳锁定

• 水星（3:2的自旋轨道共振）

被地球锁定

• 月球

被火星锁定

• 火卫一（Phobos）
• 火卫二（Deimos）

被木星锁定

• 木卫十六（Metis）
• 木卫十五（Adrastea）
• 木卫五（Amalthea）
• 木卫十四（Thebe）
• 木卫一（Io）
• 木卫二（Europa）
• 木卫三（Ganymede）
• 木卫四（Callisto）

被土星锁定

• 土卫十八（Pan）
• 土卫十五（Atlas）
• 土卫十六（Prometheus）
• 土卫十七（Pandora）
• 土卫十一（Epimetheus）
• 土卫十（Janus）
• 土卫一（Mimas）
• 土卫二（Enceladus）
• 土卫十三（Telesto）
• 土卫三（Tethys）
• 土卫十四（Calypso）
• 土卫四（Dione）
• 土卫五（Rhea）
• 土卫六（Titan）
• 土卫八（Iapetus）

被天王星锁定

• 天卫五（Miranda）
• 天卫一（Ariel）
• 天卫二（Umbriel）
• 天卫三（Titania）
• 天卫四（Oberon）

被海王星锁定

• 海卫八（Proteus）
• 海卫一（Triton）

与冥王星锁定

• 冥卫一（Charon，冥王星本身也被冥卫一锁定）

系外太阳系

• 右摄提二b（牧夫座τb）已知是因为轨道太靠近而被右摄提二（牧夫座τ）锁定的大行星

疑似被锁定的天体

太阳系

以主星锁定一个天体所需要的可能时间为基础，和它存在于轨道上的时间比较（太阳系大多数卫星的年龄与行星年龄相似），许多卫星被认为是被锁定的。但是，其中有些的自转周期还不知道或是所知不多，它们是：

可能被土星锁定

• 土卫三十五（Daphnis）
• 土卫三十二（Methone）
• 土卫三十三（Pallene）
• 土卫十二（Helene）
• 土卫三十四（Polydeuces）

可能被天王星锁定

• 天卫六（Cordelia）
• 天卫七（Ophelia）
• 天卫八（Bianca）
• 天卫九（Cressida）
• 天卫十（Desdemona）
• 天卫十一（Juliet）
• 天卫十二（Portia）
• 天卫十三（Rosalind）
• 天卫二十七（Cupid）
• 天卫十四（Belinda）
• 天卫二十五（Perdita）
• 天卫十五（Puck）
• 天卫二十六（Mab）
• 天卫四（Oberon）

可能被海王星锁定

• 海卫三（Naiad）
• 海卫四（Thalassa）
• 海卫五（Despina）
• 海卫六（Galatea）
• 海卫七（Larissa）

系外太阳系

• 南门二Bb（半人马座α Bb）可能被它的母恒星南门二B潮汐锁定。

• 格利泽581c, 格利泽581g, 格利泽581b,和格利泽581e可能被它们的母恒星格利泽581潮汐锁定。格利泽581d几乎可以确定被母恒星格利泽581锁定，不是2：1共振，就是3：2共振
• 比邻星b可能被它的母星比邻星潮汐锁定。

相关条目

• 角动量
• 重力梯度稳定
• 轨道共振
• 行星适居性
• 洛希极限
• 同步轨道
• 潮汐加速