维基百科

立方截角立方八面体

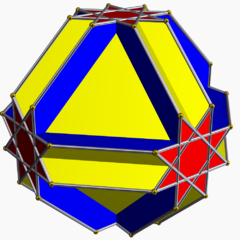
在几何学中，立方截角立方八面体是一种星形均匀多面体，由8个正六边形、6个正八边形和6个正八角星所组成[6][7][8]，其索引为U16，对偶多面体为四重二方六面体（维基数据所列：Q18048480）[1]，具有八面体群对称性（英语：Octahedral symmetry）。[9]

立方截角立方八面体
立方截角立方八面体
类别均匀星形多面体
对偶多面体四重二方六面体（维基数据所列：Q18048480）
识别
名称立方截角立方八面体
cubitruncated cuboctahedron
cuboctatruncated cuboctahedron
参考索引U16, C52, W79
鲍尔斯缩写
（verse-and-dimensions的wikia：Bowers acronym）		cotco在维基数据编辑
数学表示法
威佐夫符号
（英语：Wythoff symbol）		3 4 4/3 |
3 4/3 4 |[1][2]:121
4/3 3 4 |[3][4][5]
性质
面20
边72
顶点48
欧拉特征数F=20, E=72, V=48 （χ=-4）
组成与布局
面的种类8个正六边形
6个正八边形
6个正八角星
顶点图6.8.8/3
对称性
对称群Oh, [4,3], *432
图像
立体图
6.8.8/3
（顶点图）

四重二方六面体（维基数据所列：Q18048480）
（对偶多面体）

性质 编辑

立方截角立方八面体共由20个面、72条边和48个顶点组成[9][10][4][5]。在其20个面中，有8个正六边形、6个正八边形和6个正八角星[6][7][8]。在其48个顶点中，每个顶点都是1个正六边形、1个正八边形和1个正八角星的公共顶点，且这些面依照正六边形、正八边形和正八角星的顺序排列，在顶点图中可以用[6,8,8/3][11]或(8/3.6.8)[12][13][4]来表示。若将立方截角立方八面体作为一个简单多面体，也就是将自相交的部分分离开来，则这个立体会有62个外部面[6]。

表示法 编辑

立方截角立方八面体在考克斯特—迪肯符号（英语：Coxeter-Dynkin diagram）中可以表示为    [3]（x4/3x3x4*a）[14]，在威佐夫记号中可以表示为3 4/3 4 |[1][2]:121或4/3 3 4 |[3][4][5]。

分类 编辑

由于立方截角立方八面体的顶点图为不等边三角形且具备点可递的特性，同时，其存在自相交的面，并可以透过星形正多面体进行广义截角来构造，因此立方截角立方八面体是一种自相交截角拟正多面体（Self-Intersecting Truncated Quasi-Regular Polyhedra）。自相交截角拟正多面体一共有五种，分别为立方截角立方八面体、星形截角截半立方体、二十面截角十二面十二面体、截角截半大十二面体和大截角截半二十面体。[15]这些立体由阿尔伯特·巴杜罗（Albert Badoureau）和约翰·皮奇（Johann Pitsch）于1881年发现并描述。[16][17]

尺寸 编辑

若立方截角立方八面体的边长为单位长，则其外接球半径为七的平方根的一半：[18]

 

边长为单位长的立方截角立方八面体，中分球半径为六的平方根的一半：[8][7]

 

二面角 编辑

立方截角立方八面体有三种二面角，分别为八边形和六边形的二面角、八边形和八角星的二面角以及八角星和六边形的二面角。[11][8]

其中，八边形和八角星的二面角为直角，即90度角[11][8]；而八边形和六边形的二面角为3的平方根之倒数的反余弦值，约为54.735610度：[11][8]

 八边形 六边形 [11] [8] 0.9553166181245 54.735610317°[8]

八角星和六边形的二面角为负3的平方根之倒数的反余弦值，约为125.264390度：[11][8]

 八角星 六边形 [11] [8] 2.186276035 125.264389683°[8]

凸包 编辑

立方截角立方八面体的凸包是一个非均匀的大斜方截半立方体，其六边形面由等角但不等边的六边形组成。[7][19]

 
凸包
（等角六边形面） 		 
立方截角立方八面体

正交投影 编辑

 

顶点座标 编辑

立方截角立方八面体的顶点座标为下列座标的全排列：[8]

(±(√2−1), ±1, ±(√2+1))

参见 编辑

参考文献 编辑

  1. ^ 1.0 1.1 1.2 Weisstein, Eric W. (编). Cubitruncated Cuboctahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 
  2. ^ 2.0 2.1 Wenninger, M.J. Polyhedron Models. Cambridge University Press. 1974 [2021-09-05]. ISBN 9780521098595. LCCN 69010200. （原始内容存档于2021-08-31）. 
  3. ^ 3.0 3.1 3.2 Klitzing, Richard. Axial-Symmetrical Edge-Facetings of Uniform Polyhedra (PDF). tic. 2002, 2 (4): 3 [2022-08-20]. （原始内容存档 (PDF)于2022-08-14）. 
  4. ^ 4.0 4.1 4.2 4.3 Zvi Har'El. Kaleido Data: Uniform Polyhedron #21, cubitruncated cuboctahedron. harel.org.il. 2006-11-14 [2022-08-14]. （原始内容存档于2022-08-20）. 
  5. ^ 5.0 5.1 5.2 Paul Bourke. Uniform Polyhedra (80). Math Consult AG. October 2004 [2019-09-27]. （原始内容存档于2013-09-02）. 
  6. ^ 6.0 6.1 6.2 Robert Webb. Cubitruncated Cuboctahedron. software3d.com. [2022-08-20]. （原始内容存档于2021-03-02）. 
  7. ^ 7.0 7.1 7.2 7.3 Jürgen Meier. 11.14. Cubitruncated cuboctahedron. 3d-meier.de. [2022-08-20]. （原始内容存档于2022-08-20） （德语）. 
  8. ^ 8.00 8.01 8.02 8.03 8.04 8.05 8.06 8.07 8.08 8.09 8.10 8.11 David I. McCooey. Self-Intersecting Truncated Quasi-Regular Polyhedra: Cubitruncated Cuboctahedron. [2022-08-20]. （原始内容存档于2022-02-14）. 
  9. ^ 9.0 9.1 Maeder, Roman. 16: cubitruncated cuboctahedron. MathConsult. [2022-08-20]. （原始内容存档于2015-03-29）. 
  10. ^ V.Bulatov. cubitruncated cuboctahedron. [2022-08-20]. （原始内容存档于2021-02-28）. 
  11. ^ 11.0 11.1 11.2 11.3 11.4 11.5 11.6 Richard Klitzing. cuboctatruncated cuboctahedron, cubitruncated cuboctahedron , cotco. bendwavy.org. [2022-08-20]. （原始内容存档于2022-10-27）. 
  12. ^ Kovič, J. Classification of uniform polyhedraby their symmetry-type graphs (PDF). Int. J. Open Problems Compt. Math. 2012, 5 (4) [2022-08-20]. （原始内容存档 (PDF)于2022-08-14）. 
  13. ^ Jim McNeill. Augmenting the cubitruncated cuboctahedron. orchidpalms.com. [2022-08-20]. （原始内容存档于2012-06-05）. 
  14. ^ Richard Klitzing. Octahedral Symmetries uniform polyhedra, Polytopes & their Incidence Matrices. bendwavy.org. [2022-08-07]. （原始内容存档于2018-07-07）. 
  15. ^ David I. McCooey. Self-Intersecting Truncated Quasi-Regular Polyhedra. [2022-08-20]. （原始内容存档于2022-02-14）. 
  16. ^ Jean Paul Albert Badoureau. Mémoire sur les Figures Isocèles. Journal de l'École polytechnique. 1881, (49): 47–172. 
  17. ^ Johann Pitsch. Über Halbreguläre Sternpolyeder. Zeitschrift für das Realschulwesen. 1881, (6): 9–24, 64–65, 72–89, 216. 
  18. ^ Eric W. Weisstein. Cubitruncated Cuboctahedron. archive.lib.msu.edu. 1999-05-25 [2022-08-20]. （原始内容存档于2021-12-03）. 
  19. ^ Allen Liu. The Stars Above Us: Regular and Uniform Polytopes up to Four Dimensions (PDF). math.harvard.edu. [2022-08-20]. （原始内容存档 (PDF)于2021-12-01）. 
取自“https://zh.wikipedia.org/w/index.php?title=立方截角立方八面體&oldid=80501939”