位错
位错(英语:dislocation),在材料科学中,指晶体材料的一种内部微观缺陷,即原子的局部不规则排列(晶体缺陷)。从几何角度看,位错属于一种线缺陷,可视为晶体中已滑移部分与未滑移部分的分界线,其存在对材料的物理性能,尤其是力学性能,具有极大的影响。“位错”这一概念最早由意大利数学家和物理学家维托·伏尔特拉于1905年提出[1]。
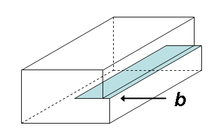
理想位错主要有三种形式:刃位错(edge dislocation)和 螺旋位错(screw dislocation)及混合位错(mixed dislocation)兼有前面两者的特征。
数学上,位错属于一种拓扑缺陷,有时称为“孤立子”或“孤子”。这一理论可以解释实际晶体中位错的行为:可以在晶体中移动位置,但自身的种类和特征在移动中保持不变;方向(伯格斯矢量)相反的两个位错移动到同一点,则会双双消失,或称“湮灭”,若没有与其他位错发生作用或移到晶体表面,那么任何单个位错都不会自行“消失”(即伯格斯矢量始终保持守恒)。
位错的几何概念
编辑刃位错和螺位错是主要的两种位错类型。然而实际晶体中存在的位错往往是混合型位错,即兼具刃型和螺型位错的特征。
晶体材料由规则排列的原子构成,一般把这些原子抽象成一个个体积可忽略的点,把它们排列成的有序微观结构称为空间点阵。逐层堆垛的原子构成一系列点阵平面的,称为晶面(可以将晶体中原子的排列情况想像成把橙子规则地装进箱子里的样子)。具体的排列情况如图2所示。在无位错的晶体(完整晶体)中,晶面(图2中的红色平行四边形)以等间距规则地排列。
刃位错
编辑若一个晶面在晶体内部突然终止于某一条线处,则称这种不规则排列为一个刃位错。如图3和图4所示,刃位错附近的原子面会发生朝位错线方向的扭曲以致错位。刃位错可由两个量唯一地确定:第一个是位错线,即多余半原子面终结的那一条直线;第二个是伯格斯矢量(Burgers vector,简称伯氏矢量或柏氏矢量),它描述了位错导致的原子面扭曲的大小和方向。对刃位错而言,其伯氏矢量方向垂直于位错线的方向。
其中 μ 为材料的剪切模量,b 为伯格斯矢量,ν 为泊松比,x 和 y 为直角坐标分量。 从上述解中可以看出,在含有多余半原子面的一侧( ),材料承受压应力( );在多余半原子面“消失”的一侧( ),材料承受拉应力( )[2]。
螺旋位错
编辑如图5所示,将规则排列的晶面想象成一叠间距固定的纸片,若将这叠纸片剪开(但不完全剪断),然后将剪开的部分其中一侧上移半层,另一侧下移半层,形成一个类似于楼梯拐角处的排列结构,则此时在“剪开线”终结处(这里已形成一条垂直纸面的位错线)附近的原子面将发生畸变,这种原子不规则排列结构称为一个螺旋位错。
可以看出,螺旋位错的伯氏矢量平行于其位错线方向。
尽管形象不甚直观,但螺旋位错的应力场却远比刃位错的应力场容易求解。在一级近似下,螺旋位错应力场只有一个剪应力分量不为零:[3]
式中 μ 为材料的剪切模量,b 为伯氏矢量,r 为所在点的极坐标极轴分量。 该应力解显示,螺旋位错附近的应力场呈轴对称式分布,大小从内到外递减。但需要注意的是在位错核心区(r=0)处按上述解将得出应力无穷大,这是不符合实际情况的。因此上述应力表达式不适用于位错核心的严重畸变区。[3]
混合位错
编辑如前所述,刃位错的伯氏矢量垂直于位错线的方向,螺位错的伯氏矢量平行于其位错线方向。但实际材料中位错的伯氏矢量往往既非平行又非垂直于位错线方向,这些位错兼具了刃位错和螺旋位错的特征,称为混合位错。
位错的观测
编辑间接观测
编辑若材料中的位错线与材料表面相交(俗称位错“露头”),则交点处附近由于位错应力场的存在,其化学稳定性将低于表面的其它部分。若用酸性腐蚀剂(如氢氟酸和硝酸的混合溶液)对这样的表面进行腐蚀,则位错“露头”处的腐蚀速度将远高于其它部分,可形成一个“腐蚀坑”。再利用一些表面显微观察技术(如扫描电子显微镜、干涉显微镜等等)便可以观察到位错的“露头”位置。图6中展示了在干涉显微镜下,经上述方法制备得到硅片表面位错腐蚀坑的形态,根据腐蚀坑边缘的形状可以确定硅片的晶体学取向——椭圆形代表硅片表面为(100)晶面,三角形代表硅片表面为(111)晶面。
若施加外力令材料发生一系列微小变形,则每次变形后某一特定位错都将处于不同的位置。如果每次变形后都对材料表面进行腐蚀,则同一位错形成的一系列腐蚀坑将粗略地显示出位错运动的轨迹。
进行上述观测的前提是材料表面能加工到具有足够高的光洁度,或者说足够低的粗糙度。
-
图6-1:(100)硅片表面的位错
-
图6-2:(111)硅片表面的位错
-
图6-3:(121)硅片表面的位错
直接观测
编辑利用透射电子显微镜(transmission electron microscope,简称TEM)可直接观察到材料微结构中的位错。TEM观察的第一步是将金属样品加工成电子束可以穿过的薄膜。在没有位错存在的区域,电子通过等间距规则排列的各晶面时将可能发生衍射,其衍射角、晶面间距及电子波长之间满足布拉格定律(Bragg's law)。而在位错存在的区域附近,晶格发生了畸变,因此衍射强度亦将随之变化,于是位错附近区域所成的像便会与周围区域形成衬度反差,这就是用TEM观察位错的基本原理,因上述原因造成的衬度差称为衍射衬度。
在图7和图8中,中间稍亮区域(晶粒)里的暗线就是所观察到位错的像。由于多晶材料中不同晶粒的晶体学取向不同,因此晶粒之间亦存在衬度差别,这就是图7和图8中中间区域较周围区域更亮的原因。值得注意的是,图中位错像所具有的“蜿蜒”的形态,这是位错线在厚度方向穿过试样(薄膜)的位错在TEM下的典型形态;还需注意的是图中位错像的终结处实际上是因为位错线到达了试样表面,而非终结在了试样内部。所有位错都只能以位错环的形式终结于晶粒的内部。
用TEM观察位错时,放大倍数一般选在5万到30万倍之间,这远未达到TEM放大倍数的极限。部分TEM还配有对试样进行在观察中原位加热/变形的装置,可以直接对位错的运动进行实时观察。
场离子显微镜(field ion microscopy,简称FIM)和原子探针(atom probe)技术提供了放大倍数更高(一般在300万倍以上)的观测方法,可在原子尺度对材料表面的位错进行直接观测。
位错源
编辑材料中的位错密度会随着塑性形变的进行而增加,其数量大致满足关系: ,其中 为塑性流动应力, 为位错密度。由这一关系可以推测,材料内部必然存在着位错的起源与增殖的机制,这些机制在外加应力的作用下将被激活,以提供增加的位错数。
人们已发现材料中存在以下三种位错的起源(成核)机制:均匀成核、晶界成核和界面成核,其中最后一种包括各种沉淀相、分散相或增强纤维等等。
位错的增殖机制主要也有三种机制:弗兰克-里德位错源(Frank-Read source)机制、双交滑移增殖机制,和攀移增殖机制[2]。
位错的滑移与晶体塑性
编辑在1930年代以前,材料塑性力学行为的微观机理一直是严重困扰材料科学家重大难题。1926年,苏联物理学家雅科夫·弗仑克尔(Jacov Frenkel)从理想完整晶体模型出发,假定材料发生塑性切变时,微观上对应着切变面两侧的两个最密排晶面(即相邻间距最大的晶面)发生整体同步滑移。根据该模型计算出的理论临界分剪应力τm 为[4]:
其中G 为剪切模量。一般常用金属的G 值约为104MPa~105MPa,由此算得的理论切变强度应为103MPa~104MPa。然而在塑性变形试验中,测得的这些金属的屈服强度仅为0.5~10MPa,比理论强度低了整整3个数量级。这是一个令人困惑的巨大矛盾。
1934年,埃贡·欧罗万(Egon Orowan)、迈克尔·波拉尼(Michael Polanyi)和杰弗里·因格拉姆·泰勒(Geoffrey Ingram Taylor)三位科学家几乎同时提出了塑性变形的位错机制理论,解决了上述理论预测与实际测试结果相矛盾的问题[5],[6],[7]。位错理论认为,之所以存在上述矛盾,是因为晶体的切变在微观上并非一侧相对于另一侧的整体刚性滑移,而是通过位错的运动来实现的。一个位错从材料内部运动到了材料表面,就相当于其位错线扫过的区域整体沿着该位错伯格斯矢量方向滑移了一个单位距离(相邻两晶面间的距离)。这样,随着位错不断地从材料内部发生并运动到表面,就可以提供连续塑性形变所需的晶面间滑移了。与整体滑移所需的打断一个晶面上所有原子与相邻晶面原子的键合相比,位错滑移仅需打断位错线附近少数原子的键合,因此所需的外加剪应力将大大降低。
在对材料进行“冷加工”(一般指在绝对温度低于0.3 Tm下对材料进行的机械加工,Tm 为材料熔点的绝对温度)时,其内部的位错密度会因为位错的萌生与增殖机制的激活而升高。随着不同滑移系位错的启动以及位错密度的增大,位错之间的相互交截的情况亦将增加,这将显著提高滑移的阻力,在力学行为上表现为材料“越变形越硬”的现象,该现象称为加工硬化(work hardening)或应变硬化(strain hardening)。缠结的位错常能在塑性形变初始发生时的材料中找到,缠结区边界往往比较模糊;在发生动态回复(recovery)过程后,不同的位错缠结区将分别演化成一个个独立的胞状结构,相邻胞状结构间一般有小于15°的晶体学取向差(小角晶界)。
由于位错的积累和相互阻挡所造成的应变硬化可以通过适当的热处理方法来消除,这种方法称为退火。退火过程中金属内部发生的回复或再结晶等过程可以消除材料的内应力,甚至完全恢复材料变形前的性能。
刃位错的攀移
编辑位错可以在包含了其伯格斯矢量和位错线的平面内滑移。螺位错的伯氏矢量平行于位错线,因此它可以在位错线所在的任何平面内滑移。而刃位错的伯氏矢量垂直于位错线,所以它只有一个滑移面。但刃位错还有一种在垂直于其滑移面方向上的运动方式,这就是攀移,即构成刃位错的多余半原子面的伸长或缩短。
攀移的驱动力来自于晶格中空位的运动。如图9所示,若一个空位移到了刃位错滑移面上与位错线相邻的位置上,则位错核心处的原子将有可能“跃迁”到空位处,造成半原子面(位错核心)向上移动一个原子间距,这一刃位错“吸收”空位的过程称为正攀移。若反之,有原子填充到半原子面下方,造成位错核心向下移动一个原子间距,则称为负攀移。
由于正攀移导致了多余半原子面的退缩,所以将使晶体在垂直半原子面方向收缩;反之,负攀移将使晶体在垂直半原子面方向膨胀。因此,在垂直半原子面方向施加的压应力会促使正攀移的发生,反之拉应力则会促使负攀移的发生。这是攀移与滑移在力学影响上的主要差别,因为滑移是由剪应力而非正应力促成的。
参考资料
编辑- ^ Volterra, V., "Sur l'équilibre des carps élastiques multiplement connexes", Annales Scientifiques de l'École Normale Supérieure, 1907, 24: pp. 401–517. (下载pdf (页面存档备份,存于互联网档案馆))
- ^ 2.0 2.1 2.2 刘孝敏编著,《工程材料的微细观结构和力学性能》,中国科学技术大学出版社,合肥,2003,ISBN 7-312-01572-7
- ^ 3.0 3.1 Reed-Hill, R. E., "Physical Metallurgy Principles", ISBN 0-534-92173-6, 1994
- ^ Frenkel, J., "Theory of the Elasticity Limits and Rigidity of Crystalline Bodies", Zeitschrift für Physik, 1926, 37: pp. 572
- ^ Orowan, E., "Zur Kristallplastizität", Zeitschrift für Physik, 1934, 89: pp. 605–659
- ^ Polanyi, M., "Form of lattice distortion that may render a crystal plastic", Zeitschrift für Physik, 1934, 89: pp. 660–666
- ^ Taylor, G.I., "The mechanism of plastic deformation of crystals", Proceedings of the Royal Society of London, 1934, A 145: pp. 362–404
延伸阅读
编辑- 冯端、丘第荣编,《金属物理学》第一卷《结构与缺陷》,科学出版社,北京,1987,ISBN 7-03-006431-3
- Dieter, G. E., Mechanical Metallurgy, 1986, ISBN 0-07-100406-8
- Honeycombe, R.W.K., The Plastic Deformation of Metals, 1984, ISBN 0-7131-2181-5
- Hull, D. & Bacon, D. J., Introduction to Dislocations, 1984, ISBN 0-08-028720-4
- Read, W. T. Jr., Dislocations in Crystals, 1953, ISBN 1-114-49066-0
- Kleinert, Hagen, Gauge Fields in Condensed Matter, Vol. II, "STRESSES AND DEFECTS; Differential Geometry, Crystal Melting", pp. 743-1456, World Scientific, Singapore, 1989; Paperback ISBN 9971-5-0210-0 (电子版在线阅读)
- Meyers and Chawla., Mechanical Behaviors of Materials. Prentice Hall, Inc., 1999, pp. 228-231.
外部链接
编辑- 清华大学“材料科学与工程概论”课程网上教程——位错[永久失效链接]
- Helmut Föll 教授的网站——“晶体中的缺陷”(页面存档备份,存于互联网档案馆)(英文) 第5章详细介绍位错相关知识
- 扫描隧道显微镜照片展(页面存档备份,存于互联网档案馆)(英文) 金属表面的原子尺度显微照片(包括表面位错),维也纳技术大学物理学教研组制作