四角锥数
在数学中,四角锥数,或金字塔数,是一个有形数表示有多少球堆积成一个金字塔(四角锥,如右图),这是以正方形为基础(底面为正方形)。
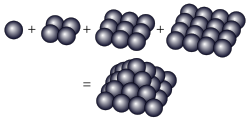
四角锥数(square pyramidal number)如右图所示,第一层+第二层+第三层+第四层每层都是正方形数合起来是正四角锥,也就是正方形数的级数。
例:1、 5(=1+4)、 14(=1+4+9)、 30(=1+4+9+16)、 55(=1+4+9+16+25)

计算方式与公式
编辑前几个四角锥数是:
这些数字可以表示为一个公式:
- 。
和其他有形数的关系
编辑四角锥数也可以表示成二项式系数的和:
两个四角锥数的总和是一个八面体数。
参见
编辑参考文献和资料来源
编辑- Abramowitz, M.; Stegun, I. A.(Eds.). Handbook of Mathematical Functions. National Bureau of Standards, Applied Math. Series 55. 1964: 813. ISBN 0486612724.
- Beiler, A. H. Recreations in the Theory of Numbers. Dover. 1964: 194. ISBN 0486210960.
- Goldoni, G. A visual proof for the sum of the first n squares and for the sum of the first n factorials of order two. The Mathematical Intelligencer. 2002, 24 (4): 67–69.
- Sigler, Laurence E.(trans.). Fibonacci's Liber Abaci. Springer-Verlag. 2002: 260–261. ISBN 0-387-95419-8.
- OELS:A000330
