莱斯分布

在概率论与数理统计领域，莱斯分布（Rice distribution或Rician distribution）是一种连续概率分布，以美国科学家斯蒂芬·莱斯的名字命名，其概率密度函数为：

Rice

概率密度函数 Rice probability density functions for various v   with σ=1. Rice probability density functions for various v   with σ=0.25.
累积分布函数 Rice cumulative density functions for various v   with σ=1. 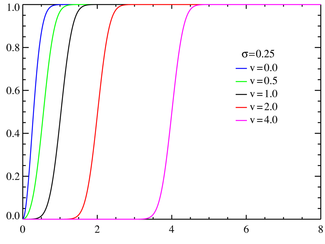Rice cumulative density functions for various v   with σ=0.25.
参数	$v\geq 0\,$ $\sigma \geq 0\,$
值域	$x\in [0;\infty )$
概率密度函数	${\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+v^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {xv}{\sigma ^{2}}}\right)$
期望值	$\sigma {\sqrt {\pi /2}}\,\,L_{1/2}(-v^{2}/2\sigma ^{2})$
方差	$2\sigma ^{2}+v^{2}-{\frac {\pi \sigma ^{2}}{2}}L_{1/2}^{2}\left({\frac {-v^{2}}{2\sigma ^{2}}}\right)$
偏度	(complicated)
峰度	(complicated)

$f(x|v,\sigma )=\,$

${\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+v^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {xv}{\sigma ^{2}}}\right)$

其中$I_{0}(z)$是修正的第一类零阶贝索函数（Bessel function）。当$v=0$时，莱斯分布退化为瑞利分布。

极限情况

For large values of the argument, the Laguerre polynomial becomes (See Abramowitz and Stegun §13.5.1 （页面存档备份，存于互联网档案馆）)

$\lim _{x\rightarrow -\infty }L_{\nu }(x)={\frac {|x|^{\nu }}{\Gamma (1+\nu )}}$

It is seen that as $v$ becomes large or $\sigma$ becomes small the mean becomes $v$ and the variance becomes $\sigma ^{2}$

相关条目

• Stephen O. Rice (1907-1986)
• 瑞利分布
• 莱斯衰落

外部链接

• Yongjun Xie and Yuguang Fang, "A General Statistical Channel Model for Mobile Satellite Systems" IEEE Transactions on Vehicular Technology, VOL. 49, NO. 3, MAY 2000. http://www.fang.ece.ufl.edu/mypaper/tvt00_xie.pdf （页面存档备份，存于互联网档案馆）