維基百科

干涉測量術

干涉測量術[1][2]（英語：interferometry）又稱干涉量度學，簡稱干涉術、干涉法，是通過由波的疊加（通常為電磁波）引起的干涉現象來獲取信息的技術[3]；其將載有被測物信息的探測光與參考光干涉，形成空域或者時域干涉條紋，從而實現光傳感、光學計量和各種光學測試技術。例如：進行精密距離和時間的測量。

圖一：邁克耳孫干涉儀中的光路。兩束由同一光源發出的光在半鍍銀鏡匯合。三個鏡子間的距離會影響兩束光在匯聚時的相位關係，產生相長或相消條紋。

干涉術這項技術對於天文學、光纖、工程計量、光學計量、海洋學、地震學、光譜學及其在化學中的應用、量子力學、核物理學、粒子物理學、 等離子體物理學、遙感、生物分子間的相互作用（英語：Interactome）、表面輪廓分析、微流控、應力與應變的測量、測速以及驗光等領域的研究都非常重要。[4]:1–2

干涉儀（interferometer）廣泛應用於科學研究和工業生產中對微小位移、折射率以及表面平整度的測量。在干涉儀中，從單個光源發出的光會分為兩束，經不同光路（英語：Optical path），最終交匯產生干涉。所產生的干涉圖紋能夠反映兩束光的光程差。在科學分析中，干涉儀用於測量長度以及光學元件的形狀，精度能到納米級。它們是現有精度最高的長度測量儀器。在傅里葉變換光譜學中，干涉儀用於分析包含與物質相互作用發生吸收或散射信息的光。天文學干涉儀（英語：astronomical interferometer）由兩個及以上的望遠鏡組成，它們的信號匯合在一起，結果的分辨率與直徑為元件間最大間距的望遠鏡的相同。

基本原理

編輯
 
圖二：邁克耳孫干涉儀中圖紋的形成。
 
圖三：邁克耳孫干涉儀產生的彩色與單色干涉紋： a圖為倒相數不同的兩束白光形成的條紋，b圖則為倒相數相同的兩束白光形成的條紋，c圖為單色光（鈉D線）形成的條紋。
更多資訊：干涉 (物理學)和邁克耳孫干涉儀

依據疊加原理，波匯合的結果具有能夠反映波原始狀態的性質。干涉測量術正是基於這一點。當兩束頻率相同的光疊加時，它們產生的條紋取決於它們的相位差：相位相同時會產生增強條紋，相反則會產生減弱條紋。兩種情況之間則會產生中間強度的條紋。這些條紋可以用來分析這兩束波的相對相位關係。絕大多數的干涉儀利用的是可見光等電磁波。[4]:3–12

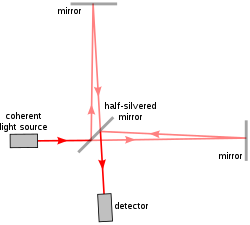
單束入射相干光在干涉儀（如圖一中的邁克耳孫干涉儀）中會經過分光鏡分為兩束。這兩束光在到達探測器重新匯聚前會各自經過不同的路徑，即光路。光路的不同會導致它們相位產生差異。干涉條紋正是產生於由此引入的相位差。[4]:14–17如果單束光分為兩路，這兩路光的相位差就可以表徵任何可能影響它們光程的因素。這些因素包括路徑長度的改變或是路徑上折射率的變化。[4]:93–103

圖二中，當觀察者透過分光鏡觀察反射鏡M1時，可以看到反射鏡M2的像M'2。所產生的圖紋可以解釋為光源S的兩個虛像S'1和S'2所發出的光而產生的干涉紋。干涉紋的特徵取決於光源的性質以及反射鏡與分光鏡的具體朝向。在圖二a中，光學元件的朝向使得S'1與S'2在觀察者眼前排成一線，所產生的干涉紋則為圓心位於M1和M'2法線上的一組同心圓。而當M1和M'2之間如在圖二b那樣存在一定傾角時，干涉紋則會變為雙曲線形，而在 M1和M'2重疊時，軸向附近的圖紋會變為彼此平行、均勻分布的直線。而當S不是圖中的點光源，而是具有一定空間外延的光源時，圖二a中的圖紋則需要在無限遠處才能觀察到，而圖二b中的圖紋則位於反射鏡上。[4]:17

當使用白光時，干涉儀則會產生如圖三中的彩色圖紋。[4]:26中心的條紋在光程相同時產生。其或亮或暗取決於兩束光在光學系統中傳播時所經歷的倒相次數。[4]:26,171–172

分類

編輯

干涉儀與干涉測量術可以依據以下原則分類：

零差檢測與外差檢測

編輯

零差檢測使用的是波長相同的兩束波。它們的相位差會導致檢測儀上光強的變化。這種檢測涉及兩束光匯合後光強的測量以及干涉紋樣式的記錄。[5]本條目中的干涉儀絕大多數屬於此類。

外差檢測用於改變輸入信號的頻率範圍或增強輸入信號（通常會用到主動混流器（英語：Electronic mixer））。頻率為f1的較弱的輸入信號會和頻率為f2的產生自本地振盪器（英語：Local Oscillator）的較強的參考信號混合在一起。這種非線性的混合會產生兩個新信號，一束的頻率為兩束輸入信號頻率之和f1 + f2，另一束的頻率則為兩束輸入信號的頻率差f1 − f2。這些新頻率稱作外差。通常檢測只會用到其中一種頻率，另一束則會自混流器輸出時被過濾掉。輸出信號的強度與輸入信號的振幅之積成比例。[5]

外差技術最為廣泛而重要的應用時美國工程師埃德溫·霍華德·阿姆斯特朗於1918年發明的超外差收音機。在這種收音機的電路中，由天線接收到的射頻信號會與本地振盪器產生的信號混流，然後通過外差技術轉換為較低的中頻信號。之後這個中頻信號會經放大以及濾波，由檢波器（英語：detector (radio)）從中提取出音頻信號輸送到揚聲器。[6]光學外差檢測（英語：Optical heterodyne detection）是外差技術向可見光頻段的延伸。[5]

雙光路與共光路

編輯
參見：共光路干涉儀
 
圖四：四種共光路干涉儀

在雙光路干涉儀中，參考光束與待檢光束沿各自的光路傳播。邁克耳孫干涉儀、特懷曼-格林干涉儀（英語：Twyman-Green interferometer）、馬赫-曾德爾干涉儀皆屬此類。待檢光束與樣品相互作用後，再和參考光束重新匯合產生用以分析的干涉圖紋。[4]:13–22

共光路干涉儀（英語：common path interferometer）中則是參考光束與樣本光束在共同的光路傳播。圖4展示了薩奈克干涉儀（英語：Sagnac effect）、光纖陀螺儀、點衍射干涉儀（英語：point diffraction interferometer）以及橫向剪切干涉儀（英語：Shearing interferometer）這四種共光路干涉儀。這類干涉儀還有澤尼克相襯顯微鏡、菲涅耳雙稜鏡、零面積薩奈克干涉儀及散射板這幾類。[7]

波前分割與波幅分割

編輯

波前分割干涉儀會在一個點或一條狹縫分割波前（可以理解為將一束光分割為兩束空間相干光），之後讓波前的這兩個部分分別經不同光路傳播之後再匯合。[8]圖五展示了楊氏干涉和勞埃德鏡這兩種波前分割機制。波前分割還有菲涅爾雙稜鏡、比耶（Billet）雙透鏡以及瑞利干涉儀（英語：Rayleigh interferometer）這幾種機制。[9]

 
圖五：兩種波前分割機制

1803年進行的楊氏干涉實驗在光的波動理論為公眾接受的過程中舉足輕重。如果實驗中使用的是白光的話，干涉結果中心會是由相長干涉（由於兩束干涉光的光路相同）造成的白色光帶，兩側則是亮度逐漸降低的對稱彩色光帶。除了連續的電磁輻射外，單光子以及電子間也會發生楊氏干涉。[10][11][12]電子顯微鏡能夠觀測到的巴基球同樣也能楊氏干涉。[13]

勞埃德鏡中則是由光源與光源的掠射像發出的光（分別是圖中的藍線與紅線）發生干涉。所產生的干涉紋並不對稱。離反射鏡最近的由同光路產生的光帶卻並不是亮的而是暗光帶。漢弗萊·勞埃德在1834年通過這個效應證明了前表面反射光束的相位發生反轉的現象。[14][15]

波幅分割干涉儀則利用部分反射鏡通過分割待測光波波幅將其分為幾束，然後在重新匯聚。圖六展示了斐索干涉儀（英語：Fizeau interferometer）、 馬赫－曾德爾干涉儀以及法布里－佩羅干涉儀。波幅分割干涉儀還有邁克耳孫干涉儀、特懷曼-格林干涉儀（英語：Twyman–Green interferometer）、激光不等光程干涉儀以及林尼克干涉儀（英語：Linnik interferometer）幾種。[16]

 
圖六：三種波幅分割干涉儀：斐索干涉儀、馬赫-曾德爾干涉儀以及法布里-佩羅干涉儀

斐索干涉儀可以用於檢測光學平面（英語：optical flat）。一個參考平面放在待檢平面之上。兩個平面之間有狹小的空隙。參考平面上表面稍稍傾斜（傾斜角在一度之內）避免後表面的干擾。待檢平面與參考平面間的空隙使得兩個平面可以成一定的傾角。這個傾角可以增添一個可控的相位梯度以形成干涉紋。人們可以以此來控制干涉紋的排布與方向，得到近乎平行的干涉紋序列而非複雜的輪廓線漩渦。不過平面的分離需要照明光準直。圖六展示了一束準直單色光照明兩個平面。分束器令干涉紋可以在軸向上觀測到。[17][18]

馬赫-曾德爾干涉儀相對於邁克耳孫干涉儀來說則更為靈活。每個光路只需走一次即可，而干涉紋也可在隨需要在任意平面上產生。[4]:18通常來說，干涉紋會被放在與待測物體相同的平面內，以使兩者可以同時被拍攝到。如果要使用白光來產生干涉紋的話，由於其相干長度有限（在微米量級），光路必須精細調整，否則不會產生可見的條紋。如圖六所示，參考光束的光路中必須放置補償單元以與待測單元匹配。同時分束器的朝向也需要精準調節。分束器的反射平面的朝向必須調整至能使待測光束與參考光束通過的玻璃的量相同。這種朝向可使兩束光都經歷兩次前表面反射，以使相位反轉數一致。最終兩束光的光程相等，產生相長的白光干涉條紋。[19][20]

法布里-佩羅干涉儀的核心是一對部分鍍銀的玻璃光學平面。兩個平面相距幾毫米或幾厘米的距離，且鍍銀面相對放置。這個裝置可以用具有兩個平行反射面的透明的法布里-佩羅標準具代替。[4]:35–36與斐索干涉儀類似，平面需要稍稍傾斜。典型配置中是由放置在凸透鏡焦平面的散射光源提供照明。如果另一側沒有對應的平面的話，那麼這樣放置會使凸透鏡產生光源的倒像，也就是說所有從點A發出的穿過光學系統的光會在點A'匯聚。圖六中只描繪了從A點發出的一束光的情況。隨着光線穿過對應的平面，它會多次反射產生多條透射光，由凸透鏡匯集，投射到屏幕上的A'點。整個干涉紋會是一組同心亮環。亮環的銳度取決於平面的反射率。如果反射率較高的話，所得到的結果Q因子也會比較高（也就是說精細度較高），人們將會看到單色光在暗背景上產生一組窄亮環。[21]圖六中，精細度較低的圖像由反射率為0.04（未鍍銀的表面）的平面產生，高精細度圖像對應的反射率則為0.95。

邁克耳孫和莫雷（1887）[22]以及同時期其他科學家都是用過干涉技術來測定以太的特性。他們在搭建系統時採用的是單色光，在實際測定中使用的則是白光。這是由於測定結果會做圖像記錄。單色光會產生均勻的干涉紋。儘管干涉儀常在地下室中搭建，然而由於缺乏控制環境溫度的有效手段，實驗者會時常經歷干涉紋的漂移。而馬車經過等等產生的震動也會使干涉紋消失。而當干涉紋重新可見時，觀察者常陷於迷茫之中。雖然白光較低的相干長度會給儀器的搭建帶來麻煩，但瑕不掩瑜，白光能產生鮮明的彩色干涉條紋的特色還是令科學家對其更為青睞。[23]這也是白光用於解決「2 模糊」的早期應用實例。

實際應用

編輯

光學干涉測量

編輯

可見光的干涉測量是干涉測量術中最先發展同時也得到最廣泛應用的類別，早期的實際應用如邁克耳孫測星干涉儀對恆星角直徑的測量，但如何獲取穩定的相干光源始終是限制光學測量發展的重要原因之一。直至二十世紀六十年代，光學干涉測量技術得到了飛速的發展，這要歸功於激光這一高強度相干光源的發明[24][25]，計算機等數字集成電路獲取並處理干涉儀所得數據的能力大大提升[26]，以及單模光纖的應用增長了實驗中的有效光程並仍能保持很低的噪聲[27]。電子技術的發展使人們不必再去觀察干涉儀產生的干涉條紋，而可以對相干光的相位差直接進行測量。這裡列舉了光學干涉測量在多個方面的一些重要應用。

長度測量

編輯
 
用於測量光程差改變，進而測定氣體折射率的瑞利干涉儀（英語：Rayleigh interferometer）[28][29]。

長度測量是光學干涉測量最常見的應用之一。如要測量某樣品的絕對長度，最簡明的方法之一是通過干涉對產生的干涉條紋進行計數；若遇到非整數的干涉條紋情形，則可以通過不斷成倍增加相干光的波長來獲得更窄的干涉條紋，直到得到滿意的測量精度為止[30][31]。常見的方法還包括惠普公司研發的惠普干涉儀[32][33]，它通過外加一個軸向磁場使氦－氖激光器 （頁面存檔備份，存於網際網路檔案館）工作在兩個相近頻率，從而發出頻率相差2兆赫茲的兩束激光，再通過偏振分束器使這兩束激光產生外差干涉。干涉得到的差頻信號被光檢測器記錄，而待測樣品引起的光程差變化則可以通過計數器表示為光波長的整數倍。惠普干涉儀可以測量在60米左右以內的長度，在附加其他光學器件後還可以用於測量角度、厚度、平直度等場合。此外，還可以通過聲光調製的方法得到差頻信號，並且這種方法能獲得更高的差頻頻率，從而可以從差頻信號中得到更高的計數。

長度測量的另一類情形是測量長度的變化，常見的方法如藉助聲光調製產生的外差干涉，差頻信號所攜帶的相位差會被光檢測器記錄，從而得到長度的變化[34]。在測量像熔凝石英這樣熱膨脹係數很低的材料的熱膨脹係數時，還經常用到一種更精確的方法：將兩面部分透射部分反射的玻璃板置於待測樣品的兩端，從而構成一個法布里－珀羅干涉儀。使用兩束髮生外差干涉的激光，並通過反饋將其中一束激光的頻率鎖定到法布里－珀羅干涉儀的一個透射峰值頻率上。這樣，當樣品發生熱膨脹而改變法布里－珀羅干涉儀的長度時，透射峰值頻率的變化會引起被鎖定的激光頻率的相應變化，這一變化也會反映到外差信號中從而被探測到[35][36]。

光學檢測

編輯
 
剪切干涉儀的光路示意圖

光學檢測包括對光學元件和光學系統的檢查和測試，諸如利用等厚干涉條紋來測量玻璃板各處的厚度，以及測量照相機鏡頭的調製傳遞函數（MTF）等都屬於這類應用。利用等厚干涉來檢測樣品表面是否平整的最常見方法是斐索干涉儀[37]，它利用準直平行光在樣品表面反射後與入射光發生干涉，從而得到等厚條紋。此外，還可以採用從邁克耳孫干涉儀改進而來的特懷曼－格林干涉儀[38]。特懷曼－格林干涉儀也使用準直平行光源，並由於從邁克耳孫干涉儀改進而來，它可以使兩束相干光的光程非常接近，從而相比於斐索干涉儀它對光源的相干長度要求有所降低。

另一類廣泛應用於檢測光學元件表面、光學系統像差以及測量光學傳遞函數的干涉儀是剪切干涉儀[39][40]，它將待測樣品出射的波前分成兩個，並使其相互錯開一定距離（這段距離被稱作剪切），兩個波前重疊的部分即產生干涉圖樣。剪切干涉儀分為切向剪切、法向剪切和旋轉剪切等類型：切向剪切干涉儀通常是一塊平行平面板或略呈角度的劈尖，準直光源入射到平行平面板上就形成了兩束錯開的相干光；而法向剪切干涉儀則類似於斐索干涉儀和特懷曼－格林干涉儀。剪切干涉儀的優點是省去了作為參考的光學表面，結構簡單且兩束相干光的光程基本相等，而缺點則是對干涉圖樣的數值分析比較繁瑣。

干涉光譜

編輯

光譜儀可分辨的兩條譜線的中心波長與恰好可分辨的波長差的比值，稱作光譜儀的色分辨本領。對利用色散效應的稜鏡光譜儀以及利用衍射效應的光柵光譜儀，其色分辨本領都不會超過106的量級[41]。然而若採用法布里－珀羅干涉儀，由於透射峰的半寬等於干涉儀的自由光譜範圍除以它的細度：

 

並由干涉條件 代入可得

 ，其中 是中心頻率。

從而法布里－珀羅干涉儀的色分辨本領為 。一般干涉序 ，細度 至少在 ，從而干涉光譜儀的色分辨本領在106至107的量級以上[42]。

干涉儀的另一個重要應用是製造波長計，波長計又分為動態波長計和靜態波長計，前者包含活動組件可調節光程差[43][44]，後者則採用光程差為倍數遞增關係的多個邁克耳孫干涉儀或自由光譜範圍為倍數遞增關係的多個法布里－珀羅干涉儀組合而成[45]。此外利用激光的外差干涉，結合法布里－珀羅干涉儀可以更精確地測量激光的頻率或比較兩束激光的頻率高低[46]，並通過聲光調製和光纖延遲還可以測量出激光的線寬[47]。

天體測量

編輯
 
位於亞利桑那州的海軍原型光學干涉儀

在邁克耳孫測星干涉儀被發明以前，恆星直徑的測量始終是天文學上的一個難題，因為已知體積最大的恆星的角直徑也只有10-2角秒。然而即使是邁克耳孫測星干涉儀，其分辨率也只能測量某些巨星的角直徑，對質量稍小的恆星就無能為力[48]。正是激光和外差干涉技術的發明，自二十世紀七十年代起在測星干涉領域引發了一場革新。在這些經改進的干涉儀中，望遠鏡捕捉到的星光與本地的激光發生外差干涉，兩者頻率非常接近，從而產生了射電頻域內的拍頻信號；並且由於這個拍頻信號的光強來自星光和激光光強的乘積，這種干涉從而能獲得更高的分辨率[49][50]。此外這些實驗大多使用了波長為10.6微米的二氧化碳激光，這也是由於較長的波長能提高外差干涉的分辨率[51]。1974年，約翰森、貝茨和唐尼斯建造了一台基線長度為5.5米的差頻干涉儀，使用了功率為1瓦特並經過穩頻的二氧化碳激光，其工作波長為10.6微米[52]。他們用這台干涉儀對一系列紅外線源進行了觀測，包括M型超巨星、米拉變星，並取得了一些星周塵殼的溫度和質量分布等信息[53][54]。而今隨着技術和製造工藝的進步，這類干涉儀的基線長度已經可以擴展到幾百米的距離，從而克服了最初邁克耳孫測星干涉儀遇到的困難[55]。

天體測量學上的另一個問題是關於天體的位置和運動的測量[56][57]。通過對恆星進行精確定位，可以將觀測到的射電源位置和它們觀測到的相應光學位置進行比對，從而直接測量它們的視差並建立宇宙距離尺度。此外這種測量還能幫助確定雙星系統軌道的尺寸和形狀。這類干涉儀包括位於亞利桑那州的海軍原型光學干涉儀（NPOI）[58]，它由四個基本部分組成Y形，彼此之間的干涉臂長度為20米，NPOI對天體的定位可以達到毫角秒的量級[59]；以及太陽系外行星天文干涉儀（ASEPS-0），它通過監視恆星因圍繞其運動的行星而引起的反映運動來研究太陽系外行星[60]。

引力波探測

編輯

引力波是廣義相對論所預言的以光速傳播的時空擾動，雖然引力波與物質的相互作用非常微弱，但已有間接的天體觀測證據表明它確實存在於諸如雙星系統這樣的天體中，並對這類天體的物理性質有着重要影響。對引力波的直接觀測不僅可以驗證廣義相對論，更重要的是提供了一種有別於基於電磁波觀測的傳統觀測天文學的新觀測手段。並且由於電磁波與引力波的不同性質，引力波天文學所研究的將是藉助電磁波無法觀測到的宇宙的另一個側面[61]。自二十世紀七十年代起，人們逐漸認識到基於干涉原理的引力波探測器是一種較有希望成功的設計，這類探測器的基本構成都是一架等臂邁克耳孫干涉儀[62][63]：本質上，激光干涉引力波探測器是對干涉臂的長度變化進行測量，並對所觀測得的數據進行分析，寄希望於尋找到其中引力波所導致的影響。即引力波所導致的干涉臂長度變化與干涉臂長度的比值：

 

其中 和 是引力波的兩個偏振態， 和 是探測器分別對這兩個偏振態的響應， 是引力波的應力強度。在實際操作中，來自外界振動、分子熱運動、以及光檢測器讀出的散粒噪聲等噪聲會疊加到觀測數據中，因而對一般來自天體的引力波而言，如要探測到它們要求探測器的靈敏度要優於 並儘可能地降低其他噪聲。通過使用較長的干涉臂同時在兩端分別增加法布里－珀羅諧振腔[64][65]，以及採用功率回收技術等方法[66][67]，可以有效地降低噪聲並提高幹涉儀的靈敏度。

 
意大利－法國聯合建造的激光干涉引力波探測器VIRGO（局部）

美國路易斯安那州和華盛頓州的激光干涉引力波天文台（LIGO）是典型的基於邁克耳孫干涉儀和法布里－珀羅諧振腔的地面引力波探測器，它被寄希望於探測到頻率在20赫茲至10千赫茲範圍內的引力波信號[68]。相同架構的地面引力波探測器還有意大利的VIRGO、德國的GEO600，日本的TAMA300以及計劃中的LCGT。美國國家航空航天局和歐洲空間局正在合作研發激光干涉空間天線（LISA）項目，計劃在太空中進行類似於邁克耳孫干涉儀的激光干涉，對低頻區域（30微赫至0.1赫茲）的引力波進行探測[69]。此外，日本正在計劃中的分赫茲干涉引力波天文台（DECIGO）同樣屬於空間計劃，人們寄希望於它能夠探測分赫茲範圍上的引力波，從而填補LIGO和LISA工作頻域之間的空白[70]。

射電干涉測量

編輯
主條目：射電天文學
 
甚大天線陣

望遠鏡的角分辨率正比於波長除以口徑，而由於無線電波的波長遠長於可見光，這造成單個射電望遠鏡無法達到觀測一般的射電源所需的分辨率（例如採用波長為2.8厘米的無線電波進行分辨率為1毫角秒的觀測，需要達6000千米的望遠鏡口徑）。基於這個原因，英國天文學家馬丁•賴爾爵士等人於1946年發明了射電干涉技術，他們用一架兩根天線組成的射電干涉儀對太陽進行了觀測[71]。射電干涉技術採用多個分立的射電望遠鏡構成陣列，這些望遠鏡在觀測時都對準同一射電發射源，各自觀測所得的信號彼此用同軸電纜、波導或光纖連接後發生干涉。這種干涉不僅僅是提升了觀測信號的強度，而且由於望遠鏡彼此間的基線距離很長，從而提升了觀測的有效口徑。由於各個望遠鏡的位置不同，同一波前到達各個望遠鏡的時間因而會存在延遲，這就需要對先到達的信號進行恰當的延遲以保持信號彼此之間的時間相干性。此外，構成干涉的望遠鏡數量越多越好，這是由於觀測射電源表面的光強分布時，兩台望遠鏡組成的干涉只能觀測到光強分布的傅立葉變換（即可見度）的各個空間頻率（這裡空間頻率的含義是描述光強在不同方向上變化快慢的傅立葉頻率）中的一個頻率；而採用多個望遠鏡構成陣列，則可以在多個空間頻率上對射電源進行觀測，再對觀測所得的可見度函數進行逆傅立葉變換得到射電源的光強分布，這種方法叫做合成孔徑[72]。例如，位於新墨西哥州的甚大天線陣（VLA）由27架射電望遠鏡組成，每架望遠鏡由直徑為25米的拋物面天線構成，彼此共形成351條彼此獨立的干涉基線，最長的等效基線可達36千米[73]。

二十世紀六十年代末，隨着射電望遠鏡接收器的性能和穩定性的提高，在全世界（以至地球軌道）範圍內使望遠鏡相距很遠的同一射電信號之間產生干涉成為可能，這被稱為超長基線干涉（VLBI）[74]。超長基線干涉不需要觀測信號之間的物理連接，而是在信號數據本身嵌入被原子鐘校準的時間信息，之後再將這些數據進行相關性計算。由於這些數據是在相隔很遠的地點觀測到的，等效基線能夠達到非常之長。現在已經運行的超長基線干涉儀包括位於美國本土及海外領地的超長基線陣列（基線長度8611千米）[75]，以及遍布歐亞和非洲大陸的歐洲超長基線干涉網[76]。這些干涉陣列平時都進行着獨立的觀測，但在一些特殊項目中可以實現同時性的觀測，從而形成全球性的超長基線干涉。

參見

編輯
 
維基共享資源上的相關多媒體資源：干涉測量術

參考文獻

編輯
  1. ^ 存档副本. [2024-01-24]. （原始內容存檔於2024-01-24）. 
  2. ^ https://terms.naer.edu.tw/detail/b300dd7ca0b216022a11474a2bb26b46/
  3. ^ Bunch, Bryan H; Hellemans, Alexander. The History of Science and Technology. Houghton Mifflin Harcourt. April 2004: 695. ISBN 978-0-618-22123-3. 
  4. ^ 4.00 4.01 4.02 4.03 4.04 4.05 4.06 4.07 4.08 4.09 Hariharan, P. Basics of Interferometry. Elsevier Inc. 2007. ISBN 0-12-373589-0. 
  5. ^ 5.0 5.1 5.2 Paschotta, Rüdiger. Optical Heterodyne Detection. RP Photonics Consulting GmbH. [1 April 2012]. （原始內容存檔於2015-03-19）. 
  6. ^ Poole, Ian. The superhet or superheterodyne radio receiver. Radio-Electronics.com. [22 June 2012]. （原始內容存檔於2018-08-19）. 
  7. ^ Mallick, S.; Malacara, D. Common-Path Interferometers. Optical Shop Testing. 2007: 97. ISBN 9780470135976. doi:10.1002/9780470135976.ch3. 
  8. ^ Verma, R.K. Wave Optics. Discovery Publishing House. 2008: 97–110 [2018-08-19]. ISBN 81-8356-114-4. （原始內容存檔於2019-08-22）. 
  9. ^ Interferential Devices – Introduction. OPI – Optique pour l'Ingénieur. [1 April 2012]. （原始內容存檔於2018-08-01）. 
  10. ^ Ingram Taylor, Sir Geoffrey. Interference Fringes with Feeble Light (PDF). Proc. Camb. Phil. Soc. 1909, 15: 114 [2 January 2013]. （原始內容存檔 (PDF)於2018-09-24）. 
  11. ^ Jönsson, C. Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten. Zeitschrift für Physik. 1961, 161 (4): 454–474. Bibcode:1961ZPhy..161..454J. doi:10.1007/BF01342460. 
  12. ^ Jönsson, C. Electron diffraction at multiple slits. American Journal of Physics. 1974, 4: 4–11. Bibcode:1974AmJPh..42....4J. doi:10.1119/1.1987592. 
  13. ^ Arndt, M.; Zeilinger, A. Heisenberg's Uncertainty and Matter Wave Interferometry with Large Molecules. Buschhorn, G. W.; Wess, J. (編). Fundamental Physics-- Heisenberg and Beyond: Werner Heisenberg Centennial Symposium "Developments in Modern Physics". Springer. 2004: 35–52 [2018-08-19]. ISBN 3540202013. （原始內容存檔於2022-01-15）. 
  14. ^ Carroll, Brett. Simple Lloyd’s Mirror (PDF). American Association of Physics Teachers. [5 April 2012]. （原始內容存檔 (PDF)於2018-09-25）. 
  15. ^ Serway, R.A.; Jewett, J.W. Principles of physics: a calculus-based text, Volume 1. Brooks Cole. 2010: 905–905 [2018-08-19]. ISBN 0-534-49143-X. （原始內容存檔於2021-08-06）. 
  16. ^ Nolte, David D. Optical Interferometry for Biology and Medicine. Springer. 2012: 17–26 [2018-08-19]. ISBN 1-4614-0889-X. （原始內容存檔於2021-08-06）. 
  17. ^ Guideline for Use of Fizeau Interferometer in Optical Testing (PDF). NASA. [8 April 2012]. （原始內容 (PDF)存檔於2018-09-25）. 
  18. ^ Interferential devices – Fizeau Interferometer. Optique pour l'Ingénieur. [8 April 2012]. （原始內容存檔於2018-08-30）. 
  19. ^ Zetie, K.P.; Adams, S.F.; Tocknell, R.M. How does a Mach–Zehnder interferometer work? (PDF). Physics Department, Westminster School, London. [8 April 2012]. （原始內容存檔 (PDF)於2018-09-25）. 
  20. ^ Ashkenas, Harry I. The design and construction of a Mach-Zehnder interferometer for use with the GALCIT Transonic Wind Tunnel. Engineer's thesis. California Institute of Technology. 1950 [2018-08-19]. （原始內容存檔於2019-05-03）. 
  21. ^ Betzler, Klaus. Fabry-Perot Interferometer (PDF). Fachbereich Physik, Universität Osnabrück. [8 April 2012]. （原始內容存檔 (PDF)於2018-09-25）. 
  22. ^ Michelson, A.A.; Morley, E.W. On the Relative Motion of the Earth and the Luminiferous Ether (PDF). American Journal of Science. 1887, 34 (203): 333–345 [2018-08-19]. doi:10.2475/ajs.s3-34.203.333. （原始內容存檔 (PDF)於2016-03-07）. 
  23. ^ Miller, Dayton C. The Ether-Drift Experiment and the Determination of the Absolute Motion of the Earth. Reviews of Modern Physics. 1933, 5 (3): 203–242. Bibcode:1933RvMP....5..203M. doi:10.1103/RevModPhys.5.203. White light fringes were chosen for the observations because they consist of a small group of fringes having a central, sharply defined black fringe which forms a permanent zero reference mark for all readings. 
  24. ^ Hariharan 2003，第79頁
  25. ^ Hariharan, P. (1987a). In 「Progress in Optics」 (E.Wolf, ed.),Vol. XXIV, pp. 105–164. Elsevier, Amsterdam.
  26. ^ Hariharan 2003，第93頁
  27. ^ Hariharan 2003，第xiii頁
  28. ^ Hariharan 2006，第15頁
  29. ^ Busch 1990，第231頁
  30. ^ Hariharan 2006，第59頁Hariharan 2003，第106-107頁
  31. ^ Bourdet, G. L., and Orszag, A. G. (1979). Appl. Opt. 18, 225–227.
  32. ^ Hariharan 2006，第59-60頁
  33. ^ J. N. Dukes and G. B. Gordon, Hewlett-Packard Journal 21, No. 12, 2–8, Dec. 1970
  34. ^ Hariharan 2006，第62頁Hariharan 2003，第116-117頁
  35. ^ Hariharan 2006，第63頁Hariharan 2003，第116頁
  36. ^ Jacobs, S. F., and Shough, D. (1981). Appl. Opt. 20, 3461–3463.
  37. ^ Hariharan 2003，第119-121頁Hariharan 2006，第67-69頁
  38. ^ Born 1999，第336-341頁Hariharan 2003，第121-122頁Hariharan 2006，第70-71頁
  39. ^ Hariharan 2003，第124-129頁Hariharan 2006，第73-77頁
  40. ^ Hopkins, H. H. (1955). Opt. Acta 2, 23–29.
  41. ^ Hariharan 2003，第157頁
  42. ^ Hariharan 2003，第159頁
  43. ^ Hariharan 2003，第165-167頁
  44. ^ Kowalski, F. V., Hawkins, R. T., and Schawlow, A. L. (1976). J. Opt. Soc. Am. 66, 965–966.
  45. ^ Hariharan 2003，第167-168頁
  46. ^ Hariharan 2003，第169頁
  47. ^ Hariharan 2003，第169-170頁
  48. ^ Born 1999，第308頁
  49. ^ Hariharan 2003，第227-230頁
  50. ^ Nieuwenhuizen, H. (1970). Mon. Not. Roy. Astron. Soc. 150, 325–335.
  51. ^ Siegman, A. E. (1966). Proc. IEEE 54, 1350–1356.
  52. ^ Johnson, M. A., Betz, A. L., and Townes, C. H. (1974). Phys. Rev. Lett. 33, 1617– 1620.
  53. ^ Sutton, E. C., Storey, J. W. V., Betz, A. L., Townes, C. H., and Spears, D. L. (1977). Astrophys. J. Lett. 217, L97.
  54. ^ Sutton, E. C. (1979). In 「High Angular Resolution Interferometry,」 Proceedings of Colloquium No. 50 of the IAU, pp. 16/1–16/14. University of Sydney, Sydney.
  55. ^ Tango, W. J., and Twiss, R. Q. (1980). In 「Progress in Optics」 (E. Wolf, ed.), Vol. XVII, pp. 241–277. North-Holland, Amsterdam.
  56. ^ Hariharan 2003，第235-238頁
  57. ^ Shao, M., and Staelin, D. H. (1977). J. Opt. Soc. Am. 67, 81–86.
  58. ^ NAVY PROTOTYPE OPTICAL INTERFEROMETER. [2015-03-02]. （原始內容存檔於2005-02-05）. 
  59. ^ Armstrong, J. T., Mozurkewich, D., Rickard, L. J., Hutter, D. J., Benson, J. A., Bowers, P. F., Elias II, N. M., Hummel, C. A., Johnston, K. J., Buscher, D. F., Clark III, J. H., Ha, L., Ling, L. C., White, N. M., and Simon, R. S. (1998). Astrophys. J. 496, 550–571.
  60. ^ Colavita, M. M., Shao, M., Hines, B. E., Wallace, J. K., Gursel, Y., Malbet, F., Yu, J. W., Singh, H., Beichman, C. A., Pan, X. P., Nakajima, T., and Kulkarni, S. R. (1994). Proc. SPIE 2200, 89–97.
  61. ^ Hariharan 2003，第241-247頁
  62. ^ Moss, G. E., Miller, L. R., and Forward, R. L. (1971). Appl. Opt. 10, 2495–2498.
  63. ^ Weiss, R. (1972). Quart. Prog. Rep. Res. Lab. Electron. M.I.T. 105, 54–76.
  64. ^ Drever, R. W. P., Hough, J., Munley, A. J., Lee, S. A., Spero, R., Whitcomb, S. E., Ward, H., Ford, G. M., Hereld, M., Robertson, N. A., Kerr, I., Pugh, J. R., Newton, G. P., Meers, B., Brooks, E. D., III, and Gursel, Y. (1981). In 「Laser Spectroscopy V」 (A. R. W. McKellar, T. Oka, and B. P. Stoicheff, eds.), pp. 33–40. Springer-Verlag, Berlin.
  65. ^ Weiss, R. (1999). Rev. Mod. Phys. 71, S187–S196.
  66. ^ Meers, B. J. (1988). Phys. Rev. D 38, 2317–2326.
  67. ^ Fritschel, P., Shoemaker, D., andWeiss, R. (1992). Appl. Opt. 31, 1412–1418.
  68. ^ LIGO Science Requirements Document (SRD) (PDF). [2010-08-24]. （原始內容 (PDF)存檔於2006-09-25）. 
  69. ^ LISA Science Requirements Document (SRD) (PDF). （原始內容 (PDF)存檔於2016-03-04）. 
  70. ^ The Japanese Space Gravitational Wave Antenna - DECIGO (PDF). （原始內容 (PDF)存檔於2010-07-27）. 
  71. ^ Thompson 2001，第12頁
  72. ^ Basics of Radio Interferometry (PDF). [2010-08-25]. （原始內容存檔 (PDF)於2008-08-27）. 
  73. ^ National Radio Astronomy Observatory. [2010-08-25]. （原始內容存檔於2017-09-13）. 
  74. ^ Thompson 2001，第304頁
  75. ^ National Radio Astronomy Observatory. [2010-08-25]. （原始內容存檔於2011-04-08）. 
  76. ^ The European VLBI Network. [2010-08-25]. （原始內容存檔於2013-03-16）. 
取自「https://zh.wikipedia.org/w/index.php?title=干涉測量術&oldid=83909160」