四方偏方面體
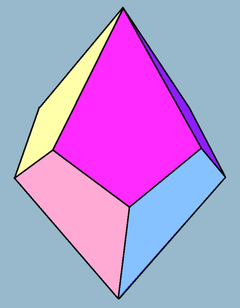
在幾何學中,四方偏方面體(英語:Tetragonal Trapezohedron)又稱為四角鳶形多面體(英語:Tetragonal Deltohedron)或雙反四角錐(英語:Tetragonal Antidipyramid)是一個由四個全等的箏形組成的立體圖形,是八面體的一種。每一個四方偏方面體也是鳶形多面體。其為反四角柱的對偶。
 | ||
| 類別 | 偏方面體 | |
|---|---|---|
| 對偶多面體 | 四角反柱 | |
| 數學表示法 | ||
| 考克斯特符號 | ||
| 性質 | ||
| 面 | 8 | |
| 邊 | 16 | |
| 頂點 | 10 | |
| 歐拉特徵數 | F=8, E=16, V=10 (χ=2) | |
| 組成與佈局 | ||
| 面的種類 | 8個箏形 | |
| 面的佈局 | V4.3.3.3 | |
| 對稱性 | ||
| 對稱群 | D4d, [2+,8], (2*4), order 16 | |
| 旋轉對稱群 | D4, [2,4]+, (224), order 8 | |
| 特性 | ||
| 凸、面可遞 | ||
| 圖像 | ||
| ||
性質
編輯四方偏方面體共由8個面、16條邊和10個頂點組成。組成四方偏方面體的8個面都是鳶形,而組成四方偏方面體的10個頂點有2個是4個鳶形的公共頂點,另外8個是3個鳶形的公共頂點。[1]
相關多面體
編輯| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|
| |
|
|
|
|
|
|
|
|
|
|
|
| 球面投影 | |||||||||||
| 對稱性 4n2 [n,4]+ |
球面鑲嵌 | 歐氏鑲嵌 | 緊湊型雙曲鑲嵌 | 仿緊型鑲嵌 | 非緊型鑲嵌 | ||||
|---|---|---|---|---|---|---|---|---|---|
| 242 [2,4]+ |
342 [3,4]+ |
442 [4,4]+ |
542 [5,4]+ |
642 [6,4]+ |
742 [7,4]+ |
842 [8,4]+... |
∞42 [∞,4]+ |
[iπ/λ,4]+ | |
| 扭稜 頂點佈局 |
3.3.4.3.2 |
3.3.4.3.3 |
3.3.4.3.4 |
3.3.4.3.5 |
3.3.4.3.6 |
3.3.4.3.7 |
3.3.4.3.8 |
3.3.4.3.∞ |
3.3.4.3.∞ |
| 考克斯特符號 施萊夫利符號 |
sr{2,4} |
sr{3,4} |
sr{4,4} |
sr{5,4} |
sr{6,4} |
sr{7,4} |
sr{8,4} |
sr{∞,4} |
rr{iπ/λ,4} |
| 扭稜 對偶 頂點佈局 |
V3.3.4.3.2 |
V3.3.4.3.3 |
V3.3.4.3.4 |
V3.3.4.3.5 |
V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ | V3.3.4.3.∞ |
| 考克斯特符號 | |||||||||
外部連結
編輯- ^ Dipyramids & Trapezohedra: Tetragonal Trapezohedron. dmccooey.com. [2022-12-29]. (原始內容存檔於2022-12-29).
