拉格朗日插值法

在數值分析中，拉格朗日插值法是以法國18世紀數學家約瑟夫·拉格朗日命名的一種多項式插值方法。許多實際問題中都用函數來表示各結果之間某種內在聯繫或規律，而不少函數都只能通過繁複實驗和多次觀測來了解。而，如果對實踐中的某個物理量進行觀測，在若干個不同的地方得到相應的觀測值，拉格朗日插值法可以找到一個多項式，其恰好在各個觀測的點取到觀測到的值。上面這樣的多項式就稱為拉格朗日（插值）多項式（Lagrange polynomial）。數學上來說，拉格朗日插值法可以給出一個恰好穿過二維平面上若干個已知點的多項式函數。拉格朗日插值法最早被英國數學家愛德華·華林於1779年發現，不久後（1783年）由萊昂哈德·歐拉再次發現。1795年，拉格朗日在其著作《師範學校數學基礎教程》中發表這個插值方法，從此他的名字就和這個方法聯繫在一起。

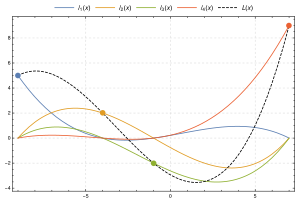
已知平面上4個點：(−9, 5), (−4, 2), (−1, −2), (7, 9)，拉格朗日多項式：L（x）（黑色）穿過所有點。而每個基本多項式：y₀ℓ₀(x), y₁ℓ₁(x), y₂ℓ₂(x)以及y₃ℓ₃(x)各穿過對應的一點，並在其它的三個點的x值上取零。

對於給定的若n+1個點$(x_{0},y_{0}),(x_{1},y_{1}),\ldots ,(x_{n},y_{n})$，對應於它們的次數不超過n的拉格朗日多項式$\scriptstyle L$只有一個。如果計入次數更高的多項式，則有無窮個，因為所有與$\scriptstyle L$相差$\lambda (x-x_{0})(x-x_{1})\ldots (x-x_{n})$的多項式都滿足條件。

定義

對某個多項式函數，已知有給定的k + 1個取值點：

$(x_{0},y_{0}),\ldots ,(x_{k},y_{k})$

其中$x_{j}$對應着自變量的位置，而$y_{j}$對應着函數在這個位置的取值。

假設任意兩個不同的x_j都互不相同，那麼應用拉格朗日插值公式所得到的拉格朗日插值多項式為：

$L(x):=\sum _{j=0}^{k}y_{j}\ell _{j}(x)$

其中每個$\ell _{j}(x)$為拉格朗日基本多項式（或稱插值基函數），其表達式為：

$\ell _{j}(x):=\prod _{i=0,\,i\neq j}^{k}{\frac {x-x_{i}}{x_{j}-x_{i}}}={\frac {(x-x_{0})}{(x_{j}-x_{0})}}\cdots {\frac {(x-x_{j-1})}{(x_{j}-x_{j-1})}}{\frac {(x-x_{j+1})}{(x_{j}-x_{j+1})}}\cdots {\frac {(x-x_{k})}{(x_{j}-x_{k})}}.$

拉格朗日基本多項式$\ell _{j}(x)$的特點是在$x_{j}$上取值為1，在其它的點$x_{i},\,i\neq j$上取值為0。

範例

假設有某個二次多項式函數$f$，已知它在三個點上的取值為：

• $f(4)=10$
• $f(5)=5.25$
• $f(6)=1$

要求$f(18)$的值。

首先寫出每個拉格朗日基本多項式：

$\ell _{0}(x)={\frac {(x-5)}{(4-5)}}\cdot {\frac {(x-6)}{(4-6)}}$

$\ell _{1}(x)={\frac {(x-4)}{(5-4)}}\cdot {\frac {(x-6)}{(5-6)}}$

$\ell _{2}(x)={\frac {(x-4)}{(6-4)}}\cdot {\frac {(x-5)}{(6-5)}}$

然後應用拉格朗日插值法，就可以得到$p$的表達式（$p$為函數$f$的插值函數）：

$p(x)=f(4)\ell _{0}(x)+f(5)\ell _{1}(x)+f(6)\ell _{2}(x)$

$.\,\,\,\,\,\,\,\,\,\,=10\cdot {\frac {(x-5)(x-6)}{(4-5)(4-6)}}+5.25\cdot {\frac {(x-4)(x-6)}{(5-4)(5-6)}}+1\cdot {\frac {(x-4)(x-5)}{(6-4)(6-5)}}$
$.\,\,\,\,\,\,\,\,\,\,={\frac {1}{4}}(x^{2}-28x+136)$

此時代入數值$\ 18$就可以求出所需之值：$\ f(18)=p(18)=-11$。

證明

存在性

對於給定的k+1個點：$(x_{0},y_{0}),\ldots ,(x_{k},y_{k})$，拉格朗日插值法的思路是找到一個在一點$x_{j}$取值為1，而在其他點取值都是0的多項式$\ell _{j}(x)$。這樣，多項式$y_{j}\ell _{j}(x)$在點$x_{j}$取值為$y_{j}$，而在其他點取值都是0。而多項式$L(x):=\sum _{j=0}^{k}y_{j}\ell _{j}(x)$就可以滿足

$L(x_{j})=\sum _{i=0}^{k}y_{i}\ell _{i}(x_{j})=0+0+\cdots +y_{j}+\cdots +0=y_{j}$

在其它點取值為0的多項式容易找到，例如：

$(x-x_{0})\cdots (x-x_{j-1})(x-x_{j+1})\cdots (x-x_{k})$

它在點$x_{j}$取值為：$(x_{j}-x_{0})\cdots (x_{j}-x_{j-1})(x_{j}-x_{j+1})\cdots (x_{j}-x_{k})$。由於已經假定$x_{i}$兩兩互不相同，因此上面的取值不等於0。於是，將多項式除以這個取值，就得到一個滿足「在$x_{j}$取值為1，而在其他點取值都是0的多項式」：

$\ell _{j}(x):=\prod _{i=0,\,i\neq j}^{k}{\frac {x-x_{i}}{x_{j}-x_{i}}}={\frac {(x-x_{0})}{(x_{j}-x_{0})}}\cdots {\frac {(x-x_{j-1})}{(x_{j}-x_{j-1})}}{\frac {(x-x_{j+1})}{(x_{j}-x_{j+1})}}\cdots {\frac {(x-x_{k})}{(x_{j}-x_{k})}}$

這就是拉格朗日基本多項式。

唯一性

次數不超過k的拉格朗日多項式至多只有一個，因為對任意兩個次數不超過k的拉格朗日多項式：$P_{1}$和$P_{2}$，它們的差$P_{1}-P_{2}$在所有k+1個點上取值都是0，因此必然是多項式$(x-x_{0})(x-x_{1})\cdots (x-x_{k})$的倍數。因此，如果這個差$P_{1}-P_{2}$不等於0，次數就一定不小於k+1。但是$P_{1}-P_{2}$是兩個次數不超過k的多項式之差，它的次數也不超過k。所以$P_{1}-P_{2}=0$，也就是說$P_{1}=P_{2}$。這樣就證明了唯一性。

幾何性質

拉格朗日插值法中用到的拉格朗日基本多項式$\ell _{0},\ell _{1},\cdots ,\ell _{n}$（由某一組$x_{0}<x_{1}<\cdots <x_{n}$確定）可以看做是由次數不超過n的多項式所組成的線性空間：$\mathbb {K} _{n}[X]$的一組基底。首先，如果存在一組系數：$\lambda _{0},\lambda _{1},\cdots ,\lambda _{n}$使得，

$P=\lambda _{0}\ell _{0}+\lambda _{1}\ell _{1}+\cdots +\lambda _{n}\ell _{n}=0$，

那麼，一方面多項式P是滿足$P(x_{0})=\lambda _{0},P(x_{1})=\lambda _{1},\cdots ,P(x_{n})=\lambda _{n}$的拉格朗日插值多項式，另一方面P是零多項式，所以取值永遠是0。所以

$\lambda _{0}=\lambda _{1}=\cdots =\lambda _{n}=0$。

這證明了$\ell _{0},\ell _{1},\cdots ,\ell _{n}$是線性無關的。同時它一共包含n+1個多項式，恰好等於$\mathbb {K} _{n}[X]$的維數。所以$\ell _{0},\ell _{1},\cdots ,\ell _{n}$構成了$\mathbb {K} _{n}[X]$的一組基底。

拉格朗日基本多項式作為基底的好處是所有的多項式都是齊次的（都是n次多項式）。

優點與缺點

拉格朗日插值法的公式結構整齊緊湊，在理論分析中十分方便，然而在計算中，當插值點增加或減少一個時，所對應的基本多項式就需要全部重新計算，於是整個公式都會變化，非常繁瑣。這時可以用重心拉格朗日插值法或牛頓插值法來代替。此外，當插值點比較多的時候，拉格朗日插值多項式的次數可能會很高，因此具有數值不穩定的特點，也就是說儘管在已知的幾個點取到給定的數值，但在附近卻會和「實際上」的值之間有很大的偏差（如右下圖）。這類現象也被稱為龍格現象，解決的辦法是分段用較低次數的插值多項式。

重心拉格朗日插值法

重心拉格朗日插值法是拉格朗日插值法的一種改進。在拉格朗日插值法中，運用多項式

$\ell (x)=(x-x_{0})(x-x_{1})\cdots (x-x_{k})$

拉格朗日插值法的數值穩定性：如圖，用於模擬一個十分平穩的函數時，插值多項式的取值可能會突然出現一個大的偏差（圖中的14至15中間）

可以將拉格朗日基本多項式重新寫為：

$\ell _{j}(x)={\frac {\ell (x)}{x-x_{j}}}{\frac {1}{\prod _{i=0,i\neq j}^{k}(x_{j}-x_{i})}}$

定義重心權

$w_{j}={\frac {1}{\prod _{i=0,i\neq j}^{k}(x_{j}-x_{i})}}$

上面的表達式可以簡化為：

$\ell _{j}(x)=\ell (x){\frac {w_{j}}{x-x_{j}}}$

於是拉格朗日插值多項式變為：

$L(x)=\ell (x)\sum _{j=0}^{k}{\frac {w_{j}}{x-x_{j}}}y_{j}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)$

即所謂的重心拉格朗日插值公式（第一型）或改進拉格朗日插值公式。它的優點是當插值點的個數增加一個時，將每個$w_{j}$都除以$(x_{j}-x_{k+1})$，就可以得到新的重心權$w_{k+1}$，計算複雜度為${\mathcal {O}}(n)$，比重新計算每個基本多項式所需要的複雜度${\mathcal {O}}(n^{2})$降了一個量級。

將以上的拉格朗日插值多項式用來對函數$g(x)\equiv 1$插值，可以得到：

$\forall x,\,g(x)=\ell (x)\sum _{j=0}^{k}{\frac {w_{j}}{x-x_{j}}}$

因為$g(x)\equiv 1$是一個多項式。

因此，將$L(x)$除以$g(x)$後可得到：

$L(x)={\frac {\sum _{j=0}^{k}{\frac {w_{j}}{x-x_{j}}}y_{j}}{\sum _{j=0}^{k}{\frac {w_{j}}{x-x_{j}}}}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)$

這個公式被稱為重心拉格朗日插值公式（第二型）或真正的重心拉格朗日插值公式。它繼承了（1）式容易計算的特點，並且在代入x值計算$L(x)$的時候不必計算多項式$\ell (x)$。它的另一個優點是，結合柴比雪夫節點進行插值的話，可以很好地模擬給定的函數，使得插值點個數趨於無窮時，最大偏差趨於零。同時，重心拉格朗日插值結合柴比雪夫節點進行插值可以達到極佳的數值穩定性。第一型拉格朗日插值是向後穩定的，而第二型拉格朗日插值是向前穩定的，並且勒貝格常數很小。

參考文獻

來源

書籍

• 李慶揚、王能超、易大義. 《数值分析》 第4版. 清華大學出版社. 2001. ISBN 7-302-04561-5 （中文（簡體））. 
• 馮有前. 《数值分析》. 清華大學出版社. 2001. ISBN 7-810-82495-3 （中文（簡體））. 
• 拉格朗日插值多项式. 太原理工大學. （原始內容存檔於2008-06-09） （中文（簡體））. 

參見

• 約瑟夫·拉格朗日
• 多項式插值
• 樣條插值
• 伯恩斯坦多項式
• 牛頓多項式
• 龍格現象