在数值分析 中,拉格朗日插值法 是以法国 18世纪数学家 约瑟夫·拉格朗日 命名的一种多项式插值 方法。许多实际问题中都用函数 来表示各结果之间某种内在联系或规律,而不少函数都只能通过繁复实验和多次观测来了解。而,如果对实践中的某个物理 量进行观测,在若干个不同的地方得到相应的观测值,拉格朗日插值法可以找到一个多项式 ,其恰好在各个观测的点取到观测到的值。上面这样的多项式就称为拉格朗日(插值)多项式 (Lagrange polynomial)。数学 上来说,拉格朗日插值法可以给出一个恰好穿过二维平面 上若干个已知点的多项式函数。拉格朗日插值法最早被英国 数学家爱德华·华林 于1779年发现[ 1] 莱昂哈德·欧拉 再次发现。1795年,拉格朗日在其著作《师范学校数学基础教程》中发表这个插值方法,从此他的名字就和这个方法联系在一起[ 2]
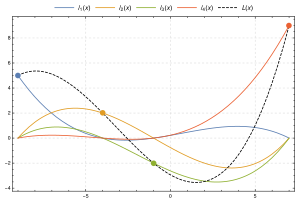
已知平面上4个点:(−9, 5) , (−4, 2) , (−1, −2) , (7, 9) ,拉格朗日多项式:L (x )y0 ℓ 0 (x ) , y1 ℓ 1 (x ) , y2 ℓ 2 (x ) 以及y3 ℓ 3 (x ) 各穿过对应的一点,并在其它的三个点的x 值上取零。 对于给定的若n+1 个点
(
x
0
,
y
0
)
,
(
x
1
,
y
1
)
,
…
,
(
x
n
,
y
n
)
{\displaystyle (x_{0},y_{0}),(x_{1},y_{1}),\ldots ,(x_{n},y_{n})}
n 的拉格朗日多项式
L
{\displaystyle \scriptstyle L}
L
{\displaystyle \scriptstyle L}
λ
(
x
−
x
0
)
(
x
−
x
1
)
…
(
x
−
x
n
)
{\displaystyle \lambda (x-x_{0})(x-x_{1})\ldots (x-x_{n})}
对某个多项式函数 ,已知有给定的k + 1个取值点:
(
x
0
,
y
0
)
,
…
,
(
x
k
,
y
k
)
{\displaystyle (x_{0},y_{0}),\ldots ,(x_{k},y_{k})}
其中
x
j
{\displaystyle x_{j}}
自变量 的位置,而
y
j
{\displaystyle y_{j}}
假设任意两个不同的x j 拉格朗日插值多项式 为:
L
(
x
)
:=
∑
j
=
0
k
y
j
ℓ
j
(
x
)
{\displaystyle L(x):=\sum _{j=0}^{k}y_{j}\ell _{j}(x)}
其中每个
ℓ
j
(
x
)
{\displaystyle \ell _{j}(x)}
拉格朗日基本多项式 (或称插值基函数 ),其表达式为:
ℓ
j
(
x
)
:=
∏
i
=
0
,
i
≠
j
k
x
−
x
i
x
j
−
x
i
=
(
x
−
x
0
)
(
x
j
−
x
0
)
⋯
(
x
−
x
j
−
1
)
(
x
j
−
x
j
−
1
)
(
x
−
x
j
+
1
)
(
x
j
−
x
j
+
1
)
⋯
(
x
−
x
k
)
(
x
j
−
x
k
)
.
{\displaystyle \ell _{j}(x):=\prod _{i=0,\,i\neq j}^{k}{\frac {x-x_{i}}{x_{j}-x_{i}}}={\frac {(x-x_{0})}{(x_{j}-x_{0})}}\cdots {\frac {(x-x_{j-1})}{(x_{j}-x_{j-1})}}{\frac {(x-x_{j+1})}{(x_{j}-x_{j+1})}}\cdots {\frac {(x-x_{k})}{(x_{j}-x_{k})}}.}
[ 3] 拉格朗日基本多项式
ℓ
j
(
x
)
{\displaystyle \ell _{j}(x)}
x
j
{\displaystyle x_{j}}
1 ,在其它的点
x
i
,
i
≠
j
{\displaystyle x_{i},\,i\neq j}
0 。
假设有某个二次多项式函数
f
{\displaystyle f}
f
(
4
)
=
10
{\displaystyle f(4)=10}
f
(
5
)
=
5.25
{\displaystyle f(5)=5.25}
f
(
6
)
=
1
{\displaystyle f(6)=1}
要求
f
(
18
)
{\displaystyle f(18)}
首先写出每个拉格朗日基本多项式:
ℓ
0
(
x
)
=
(
x
−
5
)
(
4
−
5
)
⋅
(
x
−
6
)
(
4
−
6
)
{\displaystyle \ell _{0}(x)={\frac {(x-5)}{(4-5)}}\cdot {\frac {(x-6)}{(4-6)}}}
ℓ
1
(
x
)
=
(
x
−
4
)
(
5
−
4
)
⋅
(
x
−
6
)
(
5
−
6
)
{\displaystyle \ell _{1}(x)={\frac {(x-4)}{(5-4)}}\cdot {\frac {(x-6)}{(5-6)}}}
ℓ
2
(
x
)
=
(
x
−
4
)
(
6
−
4
)
⋅
(
x
−
5
)
(
6
−
5
)
{\displaystyle \ell _{2}(x)={\frac {(x-4)}{(6-4)}}\cdot {\frac {(x-5)}{(6-5)}}}
然后应用拉格朗日插值法,就可以得到
p
{\displaystyle p}
p
{\displaystyle p}
f
{\displaystyle f}
p
(
x
)
=
f
(
4
)
ℓ
0
(
x
)
+
f
(
5
)
ℓ
1
(
x
)
+
f
(
6
)
ℓ
2
(
x
)
{\displaystyle p(x)=f(4)\ell _{0}(x)+f(5)\ell _{1}(x)+f(6)\ell _{2}(x)}
.
=
10
⋅
(
x
−
5
)
(
x
−
6
)
(
4
−
5
)
(
4
−
6
)
+
5.25
⋅
(
x
−
4
)
(
x
−
6
)
(
5
−
4
)
(
5
−
6
)
+
1
⋅
(
x
−
4
)
(
x
−
5
)
(
6
−
4
)
(
6
−
5
)
{\displaystyle .\,\,\,\,\,\,\,\,\,\,=10\cdot {\frac {(x-5)(x-6)}{(4-5)(4-6)}}+5.25\cdot {\frac {(x-4)(x-6)}{(5-4)(5-6)}}+1\cdot {\frac {(x-4)(x-5)}{(6-4)(6-5)}}}
.
=
1
4
(
x
2
−
28
x
+
136
)
{\displaystyle .\,\,\,\,\,\,\,\,\,\,={\frac {1}{4}}(x^{2}-28x+136)}
此时代入数值
18
{\displaystyle \ 18}
f
(
18
)
=
p
(
18
)
=
−
11
{\displaystyle \ f(18)=p(18)=-11}
对于给定的k +1个点:
(
x
0
,
y
0
)
,
…
,
(
x
k
,
y
k
)
{\displaystyle (x_{0},y_{0}),\ldots ,(x_{k},y_{k})}
x
j
{\displaystyle x_{j}}
1 ,而在其他点取值都是0 的多项式
ℓ
j
(
x
)
{\displaystyle \ell _{j}(x)}
y
j
ℓ
j
(
x
)
{\displaystyle y_{j}\ell _{j}(x)}
x
j
{\displaystyle x_{j}}
y
j
{\displaystyle y_{j}}
0 。而多项式
L
(
x
)
:=
∑
j
=
0
k
y
j
ℓ
j
(
x
)
{\displaystyle L(x):=\sum _{j=0}^{k}y_{j}\ell _{j}(x)}
L
(
x
j
)
=
∑
i
=
0
k
y
i
ℓ
i
(
x
j
)
=
0
+
0
+
⋯
+
y
j
+
⋯
+
0
=
y
j
{\displaystyle L(x_{j})=\sum _{i=0}^{k}y_{i}\ell _{i}(x_{j})=0+0+\cdots +y_{j}+\cdots +0=y_{j}}
在其它点取值为0 的多项式容易找到,例如:
(
x
−
x
0
)
⋯
(
x
−
x
j
−
1
)
(
x
−
x
j
+
1
)
⋯
(
x
−
x
k
)
{\displaystyle (x-x_{0})\cdots (x-x_{j-1})(x-x_{j+1})\cdots (x-x_{k})}
它在点
x
j
{\displaystyle x_{j}}
(
x
j
−
x
0
)
⋯
(
x
j
−
x
j
−
1
)
(
x
j
−
x
j
+
1
)
⋯
(
x
j
−
x
k
)
{\displaystyle (x_{j}-x_{0})\cdots (x_{j}-x_{j-1})(x_{j}-x_{j+1})\cdots (x_{j}-x_{k})}
x
i
{\displaystyle x_{i}}
0 。于是,将多项式除以这个取值,就得到一个满足“在
x
j
{\displaystyle x_{j}}
1 ,而在其他点取值都是0 的多项式”:
ℓ
j
(
x
)
:=
∏
i
=
0
,
i
≠
j
k
x
−
x
i
x
j
−
x
i
=
(
x
−
x
0
)
(
x
j
−
x
0
)
⋯
(
x
−
x
j
−
1
)
(
x
j
−
x
j
−
1
)
(
x
−
x
j
+
1
)
(
x
j
−
x
j
+
1
)
⋯
(
x
−
x
k
)
(
x
j
−
x
k
)
{\displaystyle \ell _{j}(x):=\prod _{i=0,\,i\neq j}^{k}{\frac {x-x_{i}}{x_{j}-x_{i}}}={\frac {(x-x_{0})}{(x_{j}-x_{0})}}\cdots {\frac {(x-x_{j-1})}{(x_{j}-x_{j-1})}}{\frac {(x-x_{j+1})}{(x_{j}-x_{j+1})}}\cdots {\frac {(x-x_{k})}{(x_{j}-x_{k})}}}
这就是拉格朗日基本多项式。
次数不超过k 的拉格朗日多项式至多只有一个,因为对任意两个次数不超过k 的拉格朗日多项式:
P
1
{\displaystyle P_{1}}
P
2
{\displaystyle P_{2}}
P
1
−
P
2
{\displaystyle P_{1}-P_{2}}
k +1个点上取值都是0 ,因此必然是多项式
(
x
−
x
0
)
(
x
−
x
1
)
⋯
(
x
−
x
k
)
{\displaystyle (x-x_{0})(x-x_{1})\cdots (x-x_{k})}
P
1
−
P
2
{\displaystyle P_{1}-P_{2}}
0 ,次数就一定不小于k +1。但是
P
1
−
P
2
{\displaystyle P_{1}-P_{2}}
k 的多项式之差,它的次数也不超过k 。所以
P
1
−
P
2
=
0
{\displaystyle P_{1}-P_{2}=0}
P
1
=
P
2
{\displaystyle P_{1}=P_{2}}
[ 4]
拉格朗日插值法中用到的拉格朗日基本多项式
ℓ
0
,
ℓ
1
,
⋯
,
ℓ
n
{\displaystyle \ell _{0},\ell _{1},\cdots ,\ell _{n}}
x
0
<
x
1
<
⋯
<
x
n
{\displaystyle x_{0}<x_{1}<\cdots <x_{n}}
n 的多项式所组成的线性空间 :
K
n
[
X
]
{\displaystyle \mathbb {K} _{n}[X]}
基底 。首先,如果存在一组系数 :
λ
0
,
λ
1
,
⋯
,
λ
n
{\displaystyle \lambda _{0},\lambda _{1},\cdots ,\lambda _{n}}
P
=
λ
0
ℓ
0
+
λ
1
ℓ
1
+
⋯
+
λ
n
ℓ
n
=
0
{\displaystyle P=\lambda _{0}\ell _{0}+\lambda _{1}\ell _{1}+\cdots +\lambda _{n}\ell _{n}=0}
那么,一方面多项式P 是满足
P
(
x
0
)
=
λ
0
,
P
(
x
1
)
=
λ
1
,
⋯
,
P
(
x
n
)
=
λ
n
{\displaystyle P(x_{0})=\lambda _{0},P(x_{1})=\lambda _{1},\cdots ,P(x_{n})=\lambda _{n}}
P 是零多项式,所以取值永远是0 。所以
λ
0
=
λ
1
=
⋯
=
λ
n
=
0
{\displaystyle \lambda _{0}=\lambda _{1}=\cdots =\lambda _{n}=0}
这证明了
ℓ
0
,
ℓ
1
,
⋯
,
ℓ
n
{\displaystyle \ell _{0},\ell _{1},\cdots ,\ell _{n}}
线性无关 的。同时它一共包含n+1 个多项式,恰好等于
K
n
[
X
]
{\displaystyle \mathbb {K} _{n}[X]}
ℓ
0
,
ℓ
1
,
⋯
,
ℓ
n
{\displaystyle \ell _{0},\ell _{1},\cdots ,\ell _{n}}
K
n
[
X
]
{\displaystyle \mathbb {K} _{n}[X]}
拉格朗日基本多项式作为基底的好处是所有的多项式都是齐次的(都是n 次多项式)。
拉格朗日插值法的公式结构整齐紧凑,在理论分析中十分方便,然而在计算中,当插值点增加或减少一个时,所对应的基本多项式就需要全部重新计算,于是整个公式都会变化,非常繁琐[ 5] 牛顿插值法 来代替。此外,当插值点比较多的时候,拉格朗日插值多项式的次数可能会很高,因此具有数值不稳定 的特点,也就是说尽管在已知的几个点取到给定的数值,但在附近却会和“实际上”的值之间有很大的偏差(如右下图)[ 6] 龙格现象 ,解决的办法是分段用较低次数的插值多项式。