焦耳-湯姆孫效應

焦耳-湯姆生效應是指氣體會因在等焓的環境氮氣的膨脹，而使溫度上升或下降。這個過程稱為焦耳-湯姆生過程。

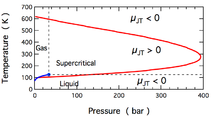
描述

各種氣體定律說明了溫度、壓力和體積。當體積不可逆回地上升，這些定律不能清楚說明壓力和溫度的改變。而在可逆絕熱過程中，氣體膨脹做了正功，因此溫度下降。

可是，真實氣體（相對理想氣體而言）在等焓環境下自由膨脹，溫度會上升或下降（是哪方看初始溫度而定）。對於給定壓力，真實氣體有一個焦耳-湯姆生反轉溫度，高於溫度時氣體溫度會上升，低於時氣體溫度下降，剛好在這溫度時氣體溫度不變。許多氣體的在1大氣壓力下的反轉溫度高於室溫。

在焦耳-湯姆生過程，溫度隨壓力的改變稱為焦耳-湯姆生系數：

\mu _{JT}=\left({\partial T \over \partial P}\right)_{H}

對於不同氣體，在不同壓力和溫度下， $\mu _{JT}$ 的值不同。 $\mu _{JT}$ 可正可負。考慮氣體膨脹，此時壓力必下降，故 $dP<0$ 。

$\mu _{JT}$ 是	因為 $dP$ 是	因此 $dT$ 必是	氣體
+	-	-	冷卻
-	-	+	變暖

若 $\mu _{JT}=0$ ，則溫度不隨壓力也不隨體積而變，此時氣體位於反轉點，而此溫度稱之反轉溫度。

氦和氫在1個大氣壓力下，反轉溫度相當低（例如氦便是−222℃）。因此，這兩種氣體在室溫膨脹時溫度上升。

對於理想氣體， $\mu _{JT}=0$ 。

溫度下降：當氣體膨脹，分子之間的平均距離上升。因為分子間吸引力，氣體的位能上升。因為這是等焓過程，系統的總能量守恆，所以位能上升必然會令動能下降，故此溫度下降。

溫度上升：當分子碰撞，動能暫時轉成位能。由於分子之間的平均距離上升，每段時間的平均碰撞次數下降，位能下降，因此動能上升，溫度上升。

低於反轉溫度時，前者的影響較為明顯，高於反轉溫度時，後者影響較明顯。

很容易證實，對於由合適的微觀假設定義的理想氣體，αT = 1，因此在焦耳-湯姆遜膨脹下這種理想氣體的溫度變化為零。對於這樣一種理想的氣體，這個理論結果意味着：

理想氣體的固定質量的內部能量僅取決於其溫度（而非壓力或體積）。

這個規則最初是由焦耳實驗發現的，它被稱為焦耳第二定律。當然，更精確的實驗發現了重要的偏差。 ^[1]^[2]^[3]

^ Partington, J.R. (1949). An Advanced Treatise on Physical Chemistry, volume 1 Fundamental Principles. The Properties of Gases, Longmans, Green and Co., London, pp. 614–615.
^ Adkins, C.J. (1968/1983). Equilibrium Thermodynamics, (1st edition 1968), third edition 1983, Cambridge University Press, Cambridge UK, ISBN 0-521-25445-0, p. 116.
^ Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 81.

Zemansky, M.W. Heat and Thermodynamics. McGraw-Hill. 1968. , p.182, 335
Schroeder, Daniel V. Thermal Physics. Addison Wesley Longman. 2000. , p.142
Kittel, C., and Kroemer, H. Thermal Physics. W.H. Freeman and Co. 1980.
Perry, R.H. and Green, D.W. Perry's Chemical Engineers' Handbook. McGraw-Hill Book Co. 1984. ISBN 978-0-07-049479-4.