自編碼器

自編碼器（英語：autoencoder）也稱自動編碼器，是一種人工神經網絡，用於學習無標籤數據的有效編碼；屬一種無監督學習。

一個具有3個全連接隱藏層的自動編碼器網絡結構。

自編碼（autoencoding）的目的是：學習對高維度數據做低維度「表示」（「表徵」或「編碼」）；因此， 通常用於降維。最近，自編碼的概念廣泛地用於數據的生成模型。 自2010年以來，一些先進的人工智能在深度學習網絡中採用了採用堆疊式稀疏自編碼。

基本結構

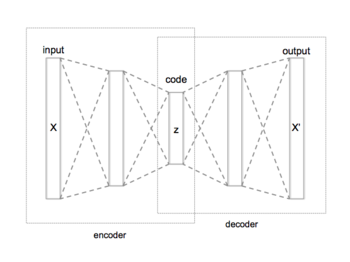
自編碼器有兩個主要部分組成：編碼器用於將輸入編碼，而解碼器使用編碼重構輸入。

實現這個功能最簡單的方式就是重複原始信號。然而，自編碼器通常被迫近似地重構輸入信號，重構結果僅僅包括原信號中最相關的部分。

自編碼器的思想已經流行了幾十年，其首次應用可以追溯到20世紀80年代。自編碼器最傳統的應用是降維或特徵學習，現在這個概念已經推廣到用於學習數據的生成模型。.21世紀10年代的一些最強大的人工智能在深度神經網絡中採用了自編碼器。

最簡單的自編碼器形式是一個前饋的、非循環的神經網絡，用一層或多層隱藏層連結輸入和輸出。輸出層節點數和輸入層一致。其目的是重構輸入（最小化輸入和輸出之間的差異），而不是在給定輸入的情況下預測目標值，所以自編碼器屬於無監督學習。

最簡單的自編碼器形式是一個前饋的、非循環的神經網絡，類似於多層感知器（MLP）中的單層感知器，用一層或多層隱藏層連結輸入和輸出。輸出層具有與輸入層相同數量的節點（神經元）。輸出層節點數和輸入層一致。其目的是重構輸入（最小化輸入和輸出之間的差異），而不是在給定輸入$X$的情況下預測目標值$Y$， 所以自編碼器屬於無監督學習。

自編碼器由編碼器和解碼器組成，二者可以被分別定義為變換 $\phi$ 和$\psi$ ，使得：

$\phi :{\mathcal {X}}\rightarrow {\mathcal {F}}$

$\psi :{\mathcal {F}}\rightarrow {\mathcal {X}}$

$\phi ,\psi ={\underset {\phi ,\psi }{\operatorname {arg\,min} }}\,\|{\mathcal {X}}-(\psi \circ \phi ){\mathcal {X}}\|^{2}$

在最簡單的情況下，給定一個隱藏層，自編碼器的編碼階段接受輸入$\mathbf {x} \in \mathbb {R} ^{d}={\mathcal {X}}$並將其映射到$\mathbf {h} \in \mathbb {R} ^{p}={\mathcal {F}}$：

$\mathbf {h} =\sigma (\mathbf {Wx} +\mathbf {b} )$

像$\mathbf {h}$通常表示編碼、潛變量或潛在表示。$\sigma$是一個逐元素的激活函數（例如sigmoid函數或線性整流函數）。$\mathbf {W}$是權重矩陣，$\mathbf {b}$是偏置向量。權重和偏置通常隨機初始化，並在訓練期間通過反向傳播迭代更新。自編碼器的解碼階段映射$\mathbf {h}$到重構$\mathbf {x'}$（與$\mathbf {x}$形狀一致）：

$\mathbf {x'} =\sigma '(\mathbf {W'h} +\mathbf {b'} )$

其中解碼器部分的$\mathbf {\sigma '} ,\mathbf {W'} ,\mathbf {b'}$ 可能與編碼器部分的$\mathbf {\sigma } ,\mathbf {W} ,\mathbf {b}$無關。

自編碼器被訓練來最小化重建誤差（如平方誤差），通常被稱為 "損失"：

${\mathcal {L}}(\mathbf {x} ,\mathbf {x'} )=\|\mathbf {x} -\mathbf {x'} \|^{2}=\|\mathbf {x} -\sigma '(\mathbf {W'} (\sigma (\mathbf {Wx} +\mathbf {b} ))+\mathbf {b'} )\|^{2}$

其中$\mathbf {x}$通常在訓練集上平均。

如前所述，和其它前饋神經網絡一樣，自編碼器的訓練是通過誤差的反向傳播進行的。

當特徵空間${\mathcal {F}}$的維度比輸入空間${\mathcal {X}}$低時，特徵向量$\phi (x)$可以看作時輸入$x$的壓縮表示，這就是不完備自動編碼（undercomplete autoencoders）的情況。如果隱藏層大於（過完備）或等於輸入層的數量，或者隱藏單元的容量足夠大，自編碼器就可能學會恆等函數而變得無用。然而，實驗結果表明過完備自編碼器（overcomplete autoencoders）仍然可能學習到有用的特徵。在理想情況下，編碼的維度和模型容量可以根據待建模數據分佈的複雜性來設定，採用這種方式的一種途徑是正則化自編碼器。

另見

• 表徵學習