逆序對

在計算機科學和離散數學中，一個序列的逆序（inversion）對，是失去自然次序的元素對。

這個置換中的一個逆序對，表示為位置對（2,4）或元素對（5,2）。
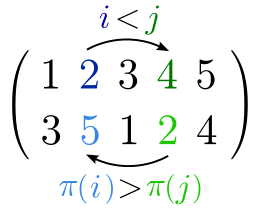
這個置換的逆序，使用基於位置表示法表示為：(1, 3), (1, 4), (2, 3), (2, 4)和(2, 5)；
或者使用基於元素表示法表示為：(3, 1), (3, 2), (5, 1), (5, 2)和(5, 4)。

定義

逆序

一個四元素置換的從基於位置逆序到基於元素逆序的映射。

設$\ \pi \$為一個排列，如果$\ i<j\$而且$\ \pi (i)>\pi (j)\$， 這個位置（有稱為「序位」）對$\ (i,j)\$，或者這個元素對$\ {\bigl (}\pi (i),\pi (j){\bigr )}\$，被稱為是$\ \pi \$的一個逆序。

逆序集是所有逆序的集合。一個排列$\ \pi \$的使用基於位置表示法的逆序集，相同於其反向排列$\ \pi ^{-1}\$的使用基於元素表示法的逆序集，只有每個有序對的兩個分量交換位置，反之亦然。

通常逆序是對於排列的定義，但也可以用於序列： 設$\ S\$是一個序列（或多重集排列）。如果$\ i<j\$而且$\ S(i)>S(j)\$， 這個位置對$\ (i,j)\$，或者這個元素對$\ {\bigl (}S(i),S(j){\bigr )}\$，被稱為是$\ S\$的一個逆序。

對於序列，根據基於元素定義的逆序不是唯一性的，因為不同的位置對上可能有相同的值對。

逆序數

序列$\ X=\langle x_{1},\dots ,x_{n}\rangle \$的逆序數$\ {\mathtt {inv}}(X)\$，是逆序集的勢，它常用於量度排列或序列的已排序程度（有時叫做預排序度presortedness）。逆序數在$\ 0\$至$\ {\frac {n(n-1)}{2}}\$之間，含二者。

在一個排列的箭頭指向圖中，它是箭頭指向相交叉的數，也是從單位排列而得到的Kendall tau距離，以及每個與逆序有關的向量之和，它們在後面章節中定義。

對於逆序數，基於位置與基於元素定義之間的分別並不重要，因為排列及其反向排列都具有相同的逆序數。

其它測量（預先）排序程度的方式，包括了為排好序列而從序列中可以刪除元素的最小數量，對序列所「運行」排序的次數和長度，每個元素在已排序位置之上的距離總和（Spearman footrule），以及排序過程中必需的最少交換次數。比較排序算法計算逆序數的時間為$\ O(n\log n)\$。

目前求逆序對數目比較普遍的方法，是利用歸併排序做到$\ O(n\log n)\$的時間複雜度；也可以利用樹狀數組、線段樹來實現這種基礎功能。複雜度均為$\ O(n\log n)\$。

逆序有關的向量

有三個類似的向量用於將排列的逆序，壓縮到能唯一確定它的這個向量中。它們通常被稱為逆序向量或Lehmer碼。這裏的定義及公式來源於逆序 (離散數學)。

本文將逆序向量記為$\ v\$，其它的兩個向量有時分別稱為「左」和「右」逆序向量；為了避免與前面的逆序向量混淆，本文將另兩個分別稱為「左逆序計數」$\ l\$和「右逆序計數」$\ r\$。左逆序計數是以反向colexicographic次序的排列，右逆序計數則是以字典序的排列。

Rothe圖

逆序向量$\ v\$：
採用基於元素的定義，$\ v(i)\$是有序對較小（右）分量為$\ i\$的逆序數。

$\ v(i)\$是在$\ \pi \$之中於$\ i\$之前，大於$\ i\$的元素的數量。

$v(i)~~=~~\#\{k\mid k>i~\land ~\pi ^{-1}(k)<\pi ^{-1}(i)\}$

其更符合直覺的定義方式為：

$\ v{\bigl (}\pi (i){\bigr )}\$是在$\ \pi \$之中於$\ \pi (i)\$之前，大於$\ \pi (i)\$的元素的數量。

$v{\bigl (}\pi (i){\bigr )}~~=~~\#\{k\mid k<i~\land ~\pi (k)>\pi (i)\}~~=~~l(i)$

後者定義也適用於沒有反向對應者的序列。

左逆序計數$\ l\$：
採用基於位置的定義，$\ l(i)\$是有序對較大（右）分量為$\ l(i)\$的逆序數。

$\ l(i)\$是在$\ \pi (i)\$之中於$\ \pi (i)\$之前，大於$\ \pi (i)\$的元素的數量。

$l(i)~~=~~\#\left\{k\mid k<i~\land ~\pi (k)>\pi (i)\right\}$

右逆序計數$\ r\$，通常稱為Lehmer碼：
採用基於位置的定義，$\ r(i)\$是有序對較小（左）分量為$\ i\$的逆序數。

$\ r(i)\$是$\ \pi (i)\$之中於$\ \pi (i)\$之後，小於$\ \pi (i)\$的元素的數量。

$r(i)~~=~~\#\{k\mid k>i~\land ~\pi (k)<\pi (i)\}$

$\ l\$和$\ v\$之間的關係：

$v(i)~~=~~l{\bigl (}\pi ^{-1}(i){\bigr )}$

$l(i)~~=~~v{\bigl (}\pi (i){\bigr )}$

$\ l\$的第一個數字和$\ v\$的最後一個數字總是$\ 0\$，可以省略。

Rothe圖可以協助找出$\ v\$和$\ r\$。Rothe圖是以黑點來表示1的排列矩陣，每一個位置上若為逆序（通常以叉號表示），則在其右側與下方即有一點。$\ r(i)\$是圖中第$\ i\$列排列逆序的加總，而$\ v(i)\$是$\ i\$欄中排列逆序的加總。排列矩陣的逆矩陣即是此矩陣的轉置矩陣，因此某一排列的$\ v\$即是它轉置矩陣的$\ r\$，反之亦然。

$\ r\$和$\ l\$之間的關係：

$\pi (i)~~=~~i+r(i)-l(i)$

範例：四個元素的全部排列

四個元素的6種可能逆序

下面可排序表顯示了四個元素的集合，它的逆序集會有不同位置的24種排列、逆序相關向量和逆序數（右欄是它的反向排列，用於以colex排序）。可以看出$\ v\$和$\ l\$的位數總是相同，而$\ l\$和$\ r\$與位逆序集有關。 最右側欄是排列左上右下對角線的總和，如三角形圖示，以及$\ r\$是左下右上對角線的總和（配對在下降對角線中其右側都是$\ 2,3,4\$組成，而在上升對角線中的左側都是$\ 1,2,3\$組成）。 此表中$\ \pi \$的預設排序是反向colex次序，這與$\ l\$的colex次序相同。$\ \pi \$的字典序與$\ r\$的字典序相同。

用於比較的三個元素全部排列表
0 1 2 3 4 5 $\pi$ $v$ $l$ p-b $r$ # 0 123 321 000 000 000 000 000 000 0 1 213 312 100 001 010 010 100 001 1 2 132 231 010 010 100 001 010 010 1 3 312 213 110 011 110 011 200 002 2 4 231 132 200 002 200 002 110 011 2 5 321 123 210 012 210 012 210 012 3

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

$\pi$ $v$ $l$ p-b $r$ # 0 1234 4321 0000 0000 0000 0000 0000 0000 0 1 2134 4312 1000 0001 0010 0100 1000 0001 1 2 1324 4231 0100 0010 0100 0010 0100 0010 1 3 3124 4213 1100 0011 0110 0110 2000 0002 2 4 2314 4132 2000 0002 0200 0020 1100 0011 2 5 3214 4123 2100 0012 0210 0120 2100 0012 3 6 1243 3421 0010 0100 1000 0001 0010 0100 1 7 2143 3412 1010 0101 1010 0101 1010 0101 2 8 1423 3241 0110 0110 1100 0011 0200 0020 2 9 4123 3214 1110 0111 1110 0111 3000 0003 3 10 2413 3142 2010 0102 1200 0021 1200 0021 3 11 4213 3124 2110 0112 1210 0121 3100 0013 4 12 1342 2431 0200 0020 2000 0002 0110 0110 2 13 3142 2413 1200 0021 2010 0102 2010 0102 3 14 1432 2341 0210 0120 2100 0012 0210 0120 3 15 4132 2314 1210 0121 2110 0112 3010 0103 4 16 3412 2143 2200 0022 2200 0022 2200 0022 4 17 4312 2134 2210 0122 2210 0122 3200 0023 5 18 2341 1432 3000 0003 3000 0003 1110 0111 3 19 3241 1423 3100 0013 3010 0103 2110 0112 4 20 2431 1342 3010 0103 3100 0013 1210 0121 4 21 4231 1324 3110 0113 3110 0113 3110 0113 5 22 3421 1243 3200 0023 3200 0023 2210 0122 5 23 4321 1234 3210 0123 3210 0123 3210 0123 6

排列的弱次序

對稱群的Permutohedron S₄

n物品排列的集合其部份次序的結構，稱為排列的弱次序，而構成格。 以逆序集的子集關係繪出的哈斯圖，則構成了稱為permutohedron的骨架。 如果依位置將某一排列分配給每個逆序集，所得到的排序是permutohedron的次序，其中的邊對應於連續兩元素的交換。這是排列的弱排序。The identity is its minimum, and the permutation formed by reversing the identity is its maximum. 如果依元素將某一排列分配給每個逆序集，所得到的排序將是凱萊圖的次序，其中的邊對應於連續兩元素的交換。對稱組的凱萊圖與其permutohedron相似，但是每個排列由其反向替換。

參見

• 階乘進制
• 置換群
• 置換的奇偶性

引用

參考書目

• Aigner, Martin. Word Representation. A course in enumeration. Berlin, New York: Springer. 2007. ISBN 978-3642072536. 
• Barth, Wilhelm; Mutzel, Petra. Simple and Efficient Bilayer Cross Counting. Journal of Graph Algorithms and Applications. 2004, 8 (2): 179–194. doi:10.7155/jgaa.00088 . 
• Bóna, Miklós. 2.2 Inversions in Permutations of Multisets. Combinatorics of permutations. Boca Raton, FL: CRC Press. 2012. ISBN 978-1439850510. 
• Comtet, Louis. 6.4 Inversions of a permutation of [n]. Advanced combinatorics; the art of finite and infinite expansions. Dordrecht,Boston: D. Reidel Pub. Co. 1974. ISBN 9027704414. 
• Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford. Introduction to Algorithms 2nd. MIT Press and McGraw-Hill. 2001. ISBN 0-262-53196-8. 
• Gratzer, George. 7-2 Basic objects. Lattice theory. special topics and applications. Cham, Switzerland: Birkhäuser. 2016. ISBN 978-3319442358. 
• Kleinberg, Jon; Tardos, Éva. Algorithm Design. 2005. ISBN 0-321-29535-8. 
• Knuth, Donald. 5.1.1 Inversions. The Art of Computer Programming. Addison-Wesley Pub. Co. 1973. ISBN 0201896850. 
• Mahmoud, Hosam Mahmoud. Sorting Nonrandom Data. Sorting: a distribution theory. Wiley-Interscience series in discrete mathematics and optimization 54. Wiley-IEEE. 2000. ISBN 978-0-471-32710-3. 
• Pemmaraju, Sriram V.; Skiena, Steven S. Permutations and combinations. Computational discrete mathematics: combinatorics and graph theory with Mathematica. Cambridge University Press. 2003. ISBN 978-0-521-80686-2. 
• Vitter, J.S.; Flajolet, Ph. Average-Case Analysis of Algorithms and Data Structures. van Leeuwen, Jan (編). Algorithms and Complexity 1 2nd. Elsevier. 1990. ISBN 978-0-444-88071-0. 

延伸閱讀

• Margolius, Barbara H. Permutations with Inversions. Journal of Integer Sequences. 2001, 4. 

預排序度測度

• Mannila, Heikki. Measures of presortedness and optimal sorting algorithms. IEEE Transactions on Computers. April 1985, C–34 (4): 318–325. doi:10.1109/tc.1985.5009382. 
• Estivill-Castro, Vladimir; Wood, Derick. A new measure of presortedness. Information and Computation. 1989, 83 (1): 111–119. doi:10.1016/0890-5401(89)90050-3 . 
• Skiena, Steven S. Encroaching lists as a measure of presortedness. BIT. 1988, 28 (4): 755–784. S2CID 33967672. doi:10.1007/bf01954897.