八元樹
八元樹(英語:Octree)是一種樹形資料結構,每個內部節點都正好有八個子節點。八元樹常用於分割三維空間,將其遞迴細分為八個卦限。八元樹是四元樹在三維空間中的對應,在三維圖形、三維遊戲引擎等領域有很多應用。
| 八元樹 | |||||
|---|---|---|---|---|---|
| 類型 | 樹 | ||||
| 發明時間 | 1980年 | ||||
| 發明者 | 唐納德·米格爾 | ||||
| 用大O符號表示的時間複雜度 | |||||
| |||||
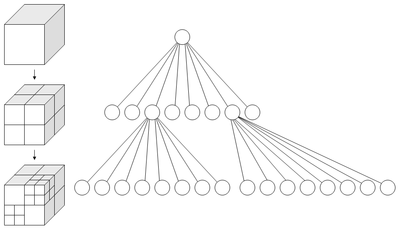
表示空間
編輯八元樹的每個節點都可以代表一個空間,對應的八個子節點則將這個空間細分為八個卦限。點域(point region,簡稱PR)八元樹的節點中都儲存著一個三維點,即該節點對應區域的「中心」,也是八個子節點對應區域中的一個角落。矩陣(matrix based,簡稱MX)八元樹中,節點只記錄區域範圍,對應的中心點坐標需要從區域範圍推算。因此,PR八元樹的根節點可以表示無限大的空間;而MX八元樹的根節點只能表示有限空間,這樣才可以得到隱含的中心點。
歷史
編輯八元樹在3D電腦圖形領域的應用可以追溯到1980年倫斯勒理工學院唐納德·馬爾(Donald Meagher)的報告《八元樹編碼:使用電腦表示、操作、顯示任意三維對象的新技術》(Octree Encoding: A New Technique for the Representation, Manipulation and Display of Arbitrary 3-D Objects by Computer)[1]。
主要用途
編輯另見
編輯- 線性八元樹
- 體素
- 四元樹
- OGRE,有基於八元樹的場景管理器
- Irrlicht引擎,支援八元樹場景節點
參考資料
編輯- ^ Meagher, Donald. Octree Encoding: A New Technique for the Representation, Manipulation and Display of Arbitrary 3-D Objects by Computer. Rensselaer Polytechnic Institute. October 1980, (Technical Report IPL-TR-80-111).
- ^ David P. Luebke. Level of Detail for 3D Graphics. Morgan Kaufmann. 2003. ISBN 978-1-55860-838-2.
- ^ Henning Eberhardt, Vesa Klumpp, Uwe D. Hanebeck, Density Trees for Efficient Nonlinear State Estimation, Proceedings of the 13th International Conference on Information Fusion, Edinburgh, United Kingdom, July, 2010. (PDF). [2018-07-03]. (原始內容存檔 (PDF)於2016-03-03).
外部連結
編輯- Octree Quantization in Microsoft Systems Journal
- Color Quantization using Octrees in Dr. Dobb's(頁面存檔備份,存於網際網路檔案館)
- Octree Color Quantization Overview(頁面存檔備份,存於網際網路檔案館)
- Parallel implementation of octtree generation algorithm, P. Sojan Lal, A Unnikrishnan, K Poulose Jacob, ICIP 1997, IEEE Digital Library(頁面存檔備份,存於網際網路檔案館)
- C++ implementation (GPL license)(頁面存檔備份,存於網際網路檔案館)
- Parallel Octrees for Finite Element Applications(頁面存檔備份,存於網際網路檔案館)
- Cube 2: Sauerbraten - a game written in the octree-heavy Cube 2 engine(頁面存檔備份,存於網際網路檔案館)
- Ogre - A 3d Object-oriented Graphics Rendering Engine with a Octree Scene Manager Implementation (MIT license)(頁面存檔備份,存於網際網路檔案館)
- Dendro: parallel multigrid for octree meshes (MPI/C++ implementation)
- Video: Use of an octree in state estimation(頁面存檔備份,存於網際網路檔案館)