瓦特曲線

瓦特曲線是指一個六次方程的平面代數曲線，也是圓代數曲線。是由二個半徑為b ，圓心之間距離為2a（分別在(±a, 0)）的圓所產生，一個長為2c的線段，兩端點分別在二圓上，其線段中間的軌跡即為瓦特曲線，此曲線和詹姆斯·瓦特在蒸汽機上的貢獻有關。

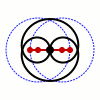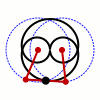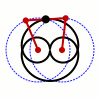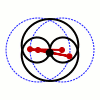繪製瓦特曲線（圖中的黑線）

瓦特曲線的方程式可以寫為以下的極坐標系方程

$r^{2}=b^{2}-\left[a\sin \theta \pm {\sqrt {c^{2}-a^{2}\cos ^{2}\theta }}\right]^{2}.$

推導

極坐標系

極坐標系方程可以用下式推導： 在複數平面上，令二圓的圓心為a和−a，二圓連線的端點為−a+be^{i λ}和a+be^{i ρ}。令線段相對水平線的斜角ψ，其中點為re^{i θ}，則二端點也可表示為re^{i θ} ± ce^{i ψ}。二端點的二種表示式可得：

$a+be^{i\rho }=re^{i\theta }+ce^{i\psi }.\,$

$-a+be^{i\lambda }=re^{i\theta }-ce^{i\psi }\,$

二式相加再除二可得

$re^{i\theta }={\tfrac {b}{2}}(e^{i\rho }+e^{i\lambda })=b\cos({\tfrac {\rho -\lambda }{2}})e^{i{\tfrac {\rho +\lambda }{2}}}.$

比較半徑及幅角可得

$r=b\cos \alpha ,\ \theta ={\tfrac {\rho +\lambda }{2}}\ {\mbox{where}}\ \alpha ={\tfrac {\rho -\lambda }{2}}.$

一開始的二式相減再除二可得

$ce^{i\psi }-a={\tfrac {b}{2}}(e^{i\rho }-e^{i\lambda })=ib\sin \alpha e^{i\theta }.$

將a以下式表示

$a=a\cos \theta \ e^{i\theta }-ia\sin \theta \ e^{i\theta }.\,$

因此

$ce^{i\psi }=ib\sin \alpha e^{i\theta }+a\cos \theta \ e^{i\theta }-ia\sin \theta \ e^{i\theta }=(a\cos \theta \ +i(b\sin \alpha -a\sin \theta ))e^{i\theta },$

$c^{2}=a^{2}\cos ^{2}\theta +(b\sin \alpha -a\sin \theta )^{2},\,$

$b\sin \alpha =a\sin \theta \pm {\sqrt {c^{2}-a^{2}\cos ^{2}\theta }},\,$

$r^{2}=b^{2}\cos ^{2}\alpha =b^{2}-b^{2}\sin ^{2}\alpha =b^{2}-\left[a\sin \theta \pm {\sqrt {c^{2}-a^{2}\cos ^{2}\theta }}\right]^{2}.,\,$

直角座標系

將極座標方式展開可得

$r^{2}=b^{2}-(a^{2}\sin ^{2}\theta \ +c^{2}-a^{2}\cos ^{2}\theta \pm 2a\sin \theta {\sqrt {c^{2}-a^{2}\cos ^{2}\theta }}),\,$

$r^{2}-a^{2}-b^{2}+c^{2}+2a^{2}\sin ^{2}\theta =\pm 2a\sin \theta {\sqrt {c^{2}-a^{2}\cos ^{2}\theta }}),\,$

$(r^{2}-a^{2}-b^{2}+c^{2})^{2}+4a^{2}(r^{2}-a^{2}-b^{2}+c^{2})\sin ^{2}\theta +4a^{4}\sin ^{4}\theta =4a^{2}\sin ^{2}\theta (c^{2}-a^{2}\cos ^{2}\theta ),\,$

$(r^{2}-a^{2}-b^{2}+c^{2})^{2}+4a^{2}(r^{2}-b^{2})\sin ^{2}\theta =0,\,$

$(x^{2}+y^{2})(x^{2}+y^{2}-a^{2}-b^{2}+c^{2})^{2}+4a^{2}y^{2}(x^{2}+y^{2}-b^{2})=0.\,$

令d ²=a²+b²–c² 因此可簡化上式為:$(x^{2}+y^{2})(x^{2}+y^{2}-d^{2})^{2}+4a^{2}y^{2}(x^{2}+y^{2}-b^{2})=0.\,$

瓦特連桿

當曲線通過原點時，原點為拐點，因此有3階接觸切線。不過若a²=b²+<c²，則有5階接觸切線，換句話說此曲線相當接近直線，這就是瓦特連桿可以作為直線運動機構的原理。

相關條目

• 平面四桿機構
• 瓦特連桿

外部連結

• 埃里克·韋斯坦因. Watt's Curve. MathWorld. 
• 約翰·J·奧康納; 埃德蒙·F·羅伯遜, Watt's Curve, MacTutor數學史檔案 （英語） 
• "Courbe de Watt" at Encyclopédie des Formes Mathématiques Remarquables （頁面存檔備份，存於網際網路檔案館） (in French)
• Catalan, E. Sur la Courbe de Watt. Mathesis. 1885, V: 154. 
• Rutter, John W. Geometry of Curves. CRC Press. 2000: 73ff. ISBN 1-58488-166-6.