等瓣原理
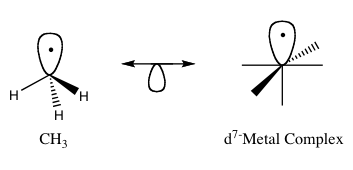
等瓣原理(英語:Isolobal princple,或者可以稱為等瓣相似原理[註 1])是一種有機金屬化學合成的策略,用於將有機與無機分子分離成碎片結構,並推測碎片間「再鍵合」成有機金屬化合物的性質。[1] 羅德·霍夫曼把兩個「數量、對稱性、近似能量、形狀及占據電子數相似的前線軌域」定義為「等瓣相似的」,它們未必是完全相同的,但十分相似。[2]對於未知有機金屬錯合物,如果其兩個碎片擁有相似的前線軌域,即最高占據分子軌域(HOMO)和最低未占據分子軌域(LUMO),便可以利用此原理推測目標分子的鍵合和反應性。等瓣相似關係以下圖中的雙向箭頭符號來表示,箭頭下帶半瓣軌域。
因為羅德·霍夫曼在等瓣近似原理上的貢獻,他與福井謙一共同分享了1981年的諾貝爾化學獎。[3]霍夫曼在諾貝爾獎演講中強調,等瓣相似原理是一種有用但簡單的模型,因此在某些情況下不能適用。[1]
構建碎片
編輯在將分子分解成等瓣碎片之前,其必須滿足一些標準[4]:當所有成鍵和非鍵分子軌域都被填滿且所有反鍵分子軌域都為空時,包含主族元素的分子應滿足八電子規則。例如,甲烷是一種可以用來構建分子碎片的簡單有機物,通過把甲烷的一個氫原子「去除」來產生一個甲基自由基,該分子保留幾何形狀,其前線軌域指向失去氫原子的方向。以此類推,可以重複此過程直至只剩下一個鍵為止。
簡單的八面體錯合物ML6的等瓣相似碎片可以以類似的方法構建,需要滿足的標準為:包含過渡金屬的錯合物應滿足18電子規則、淨電荷為零、配位基應提供一對電子(路易斯鹼)。因此,起始分子的金屬中心必須是d6組態,去除配位基的過程與上文中去除甲烷中氫的過程相似,前線軌域指向去除配位基的方向。切分金屬與配位基間的鍵後得到了ML5自由基錯合物,為了保持分子的電中性,中心金屬的一個價電子填入非鍵前線軌域,金屬變為d7。例如,MoL6錯合物的中心為d6,去除一個配位基後形成的ML−
5自由基錯合物獲得了一個額外的電子。為了滿足「淨電荷為零」的標準,可以用Mn相似替換Mo,而MnL5是電中性的d7錯合物,此過程可以重複至只餘一個與金屬相連的配位基。
四面體與八面體碎片的聯繫
編輯四面體和八面體分子的等瓣相似碎片可能是相似關聯的,凡具有相同數量前線軌域的結構是相似關聯的。例如,去除了兩個氫原子的甲烷碎片CH2和d8-ML4的八面體錯合物碎片是等瓣相似的。
分子軌域理論
編輯任何「飽和」的分子都可以作為構建等瓣相似碎片的起點,[5][6]其中成鍵、非鍵軌域應被填滿,反鍵軌域為空。隨著等瓣相似碎片的構建,電子不斷從鍵合軌域中被移除,前線軌域不斷地被創建。前線軌域的能量高於成鍵和非鍵分子軌域,每個前線軌域中都包含一個電子。
如上圖所示,當一個碎片從CH4被分離出來時,一條鍵合的sp3混成軌域變為單電子占據的前線軌域。當碎片從d6-ML6金屬錯合物中分離出來時,d2sp3混成軌域也會受到影響,不過其中一組非鍵簡併軌域t2g並沒有變化。
等瓣相似的拓展
編輯除去簡單的八面體錯合物外,等瓣相似原理可以應用於多種配位基、帶電物質和非八面體的錯合物。[7]
等電子體
編輯等瓣相似也可以用於含相同配位數的等電子碎片,允許人們對帶電荷的物質進行推測。例如,Re(CO)5與CH3等瓣相似,可以拓展為[Ru(CO)5]+或是[Mo(CO)5]−同樣是與CH3等瓣相似的。
同理,從兩個等瓣相似碎片中增加或去除電荷得到的帶電碎片同樣是等瓣相似的,例如Re(CO)5與CH3是等瓣相似的,因此[Re(CO)5]+與CH+
3是等瓣相似的。[8]
非八面體錯合物
編輯| 八面體 MLn |
平面正方形 MLn−2 |
|---|---|
| d6: Mo(CO)5 | d8: [PdCl3]− |
| d8: Os(CO)4 | d10: Ni(PR3)2 |
該相似關係能應用於四面體和八面體外的其他構型,對於大多數幾何結構,八面體的推演過程都適用。平面正方形錯合物卻是例外,譬如假設配位基提供一對電子,平面正方形的金屬中心為d8,要將其與中心金屬為dx的八面體碎片MLn等瓣相似關聯的話,應滿足dx+2- MLn-2的公式。
備註
編輯- ^ Isolobal analogy
參考文獻
編輯- ^ 1.0 1.1 Hoffmann, R. Building Bridges Between Inorganic and Organic Chemistry (Nobel Lecture) (PDF). Angew. Chem. Int. Ed. 1982, 21 (10): 711–724 [2022-06-10]. doi:10.1002/anie.198207113. (原始內容存檔 (PDF)於2016-06-24).
- ^ Elian, M.; Chen, M. M.-L.; Mingos, D. M. P.; Hoffmann, R. Comparative bonding study of conical fragments. Inorg. Chem. 1976, 15 (5): 1148–1155. doi:10.1021/ic50159a034.
- ^ The Nobel Prize in Chemistry 1981: Kenichi Fukui, Roald Hoffmann. nobelprize.org. [December 22, 2010]. (原始內容存檔於2012-11-02).
- ^ Department of Chemistry. Modern Approaches to Inorganic Bonding. University of Hull.
- ^ Gispert, Joan Ribas. Coordination Chemistry. Wiley-VCH. 2008: 172–176.
- ^ Shriver, D.F.; Atkins, P.; Overton, T.; Rourke, J.; Weller, M.; Armstrong, F. Inorganic Chemistry. Freeman. 2006.
- ^ Miessler, G. L.; Tarr, D. A. Inorganic Chemistry 3rd. Pearson Education. 2008.
- ^ Douglas, B.; McDaniel, D.; Alexander, J. Concepts and Models of Inorganic Chemistry 3rd. Wiley & Sons. 1994.