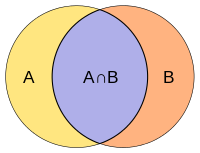
雅卡爾指數
雅卡爾指數(英語:Jaccard index),又稱為交並比(Intersection over Union)、雅卡爾相似係數(Jaccard similarity coefficient),是用於比較樣本集的相似性與多樣性的統計量。雅卡爾係數能夠量度有限樣本集合的相似度,其定義為兩個集合交集大小與併集大小之間的比例:
如果A與B完全重合,則定義J(A,B) = 1。於是有
雅卡爾距離(Jaccard distance)則用於量度樣本集之間的不相似度,其定義為1減去雅卡爾係數,即
此外,亦有人將雅卡爾距離定義兩集合對稱差的大小與併集大小之間的比例。
| 這是一篇小作品。您可以透過編輯或修訂擴充其內容。 |
參見
編輯參考文獻
編輯- ^ Sven Kosub, "A note on the triangle inequality for the Jaccard distance" arXiv:1612.02696 (頁面存檔備份,存於網際網路檔案館)
- ^ Lipkus, Alan H, A proof of the triangle inequality for the Tanimoto distance, J Math Chem, 1999, 26 (1-3): 263–265
- ^ Levandowsky, Michael; Winter, David, Distance between sets, Nature, 1971, 234 (5): 34–35, doi:10.1038/234034a0